初中数学青岛版九年级下册5.1函数与它的表示法教学演示ppt课件

这是一份初中数学青岛版九年级下册5.1函数与它的表示法教学演示ppt课件，共19页。PPT课件主要包含了学习目标，复习导入，观察与思考，2解析法，是函数关系，≤x≤40，归纳与总结，达标练习，2t10分钟，s＝2t等内容，欢迎下载使用。
1.通过实例，让学生进一步了解函数的三种表示法,知道三种表示方法各自的优、缺点；
2.在实际情景中，会根据不同的需要选择适当的方法表示函数.
1.什么是函数？2.你学习过哪些函数？3.你会用几种方法表示一次函数？
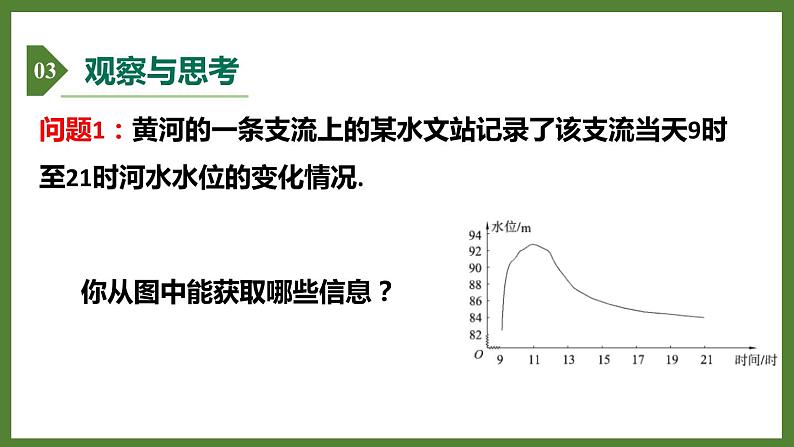
问题1：黄河的一条支流上的某水文站记录了该支流当天9时至21时河水水位的变化情况.
你从图中能获取哪些信息？
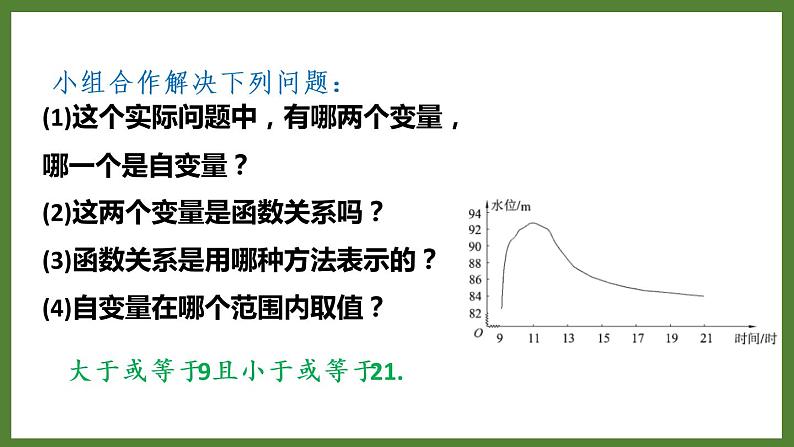
(1)这个实际问题中，有哪两个变量，哪一个是自变量？(2)这两个变量是函数关系吗？(3)函数关系是用哪种方法表示的？(4)自变量在哪个范围内取值？
大于或等于9且小于或等于21.
小组合作解决下列问题：
问题3：物体从490 m的高度处自由下落，物体距地面的高度h(m)与物体下落的时间 t(s)之间的关系满足表达式 h= 490 - 4.9t². 思考：
(1)物体距地面的高度h与物体下落的时间t之间是函数关系吗？(2)如果是，它们之间的函数关系是用哪种方法表示的？(3)其中，自变量是在哪个范围内取值的？
(3)自变量的取值范围是0≤t≤10.
小组合作，得出(3)的结果.
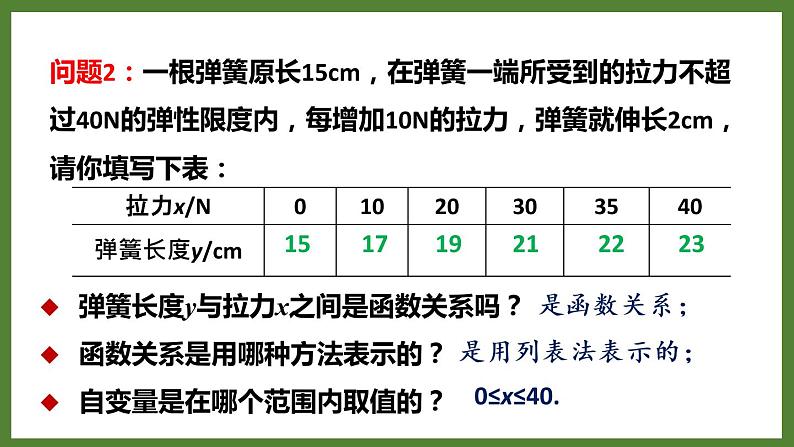
问题2：一根弹簧原长15cm，在弹簧一端所受到的拉力不超过40N的弹性限度内，每增加10N的拉力，弹簧就伸长2cm，请你填写下表：
弹簧长度y与拉力x之间是函数关系吗？函数关系是用哪种方法表示的？自变量是在哪个范围内取值的？
图象法：用图象表示函数关系；
表示两个变量之间的函数关系的方法有三种：
列表法：用表格表示函数关系；
解析法：用函数表达式表示函数关系.
三种表示方法的联合运用
(1) 请你用表格表示这个函数关系.
(2) 你能用函数解析式表示这个函数关系吗？
(3) 请大家讨论图象法的优缺点
优点：直观形象反映变化趋势；缺点：不能准确地求出函数值.
(1) 请你根据表格画出函数图象；(2) 请你写出y与x的表达式；(3) 请大家讨论表格法的优缺点.
(3)表格法优点：不通过计算即可查出部分函数值；缺点：只能表示有限个函数值，不直观.
你会用描点法画出问题3中的函数图象吗？
由问题3的实际意义和函数表达式h=490-4.9t2,先确定自变量t的取值范围是0≤t≤10.
根据函数的表达式和自变量可以取值的范围，列出下面的表格：
以时间t为横轴、高度h为纵轴画出直角坐标系(根据该问题的实际背景，横轴和纵轴选取不同的单位长度)，然后以上表中的每一个有序实数对(t，h)为坐标，在直角坐标系中描出相应的各点，用一条平滑的曲线，按自左向右的顺序顺次连接它们，便得函数y=490-4.9t2 (0≤t≤10)的图象，它是一段曲线.
表示函数关系的三种方法的优缺点：
1.一辆汽车在公路上行驶，其所走的路程和所用的时间表示为：
(1)在这个变化过程中，自变量、因变量各是什么？(2)当汽车行驶路程s为20km时，所花的时间t是多少分钟？
解：(1)自变量是时间t,因变量是路程s.
(3)从表中说出随着t逐渐变大，s的变化趋势是什么？(4)如果汽车行驶的时间为t(min)，行驶的路程为s(km)，那么路程s与时间t之间的关系式为_________．
(3)随着时间t增大，路程s也在增大
2.某商店零售一种商品，其质量x(kg)与售价y(元)之间的关系如下表：
(1)由上表推出售价y随质量x变化的函数表达式，并画出函数的图象；(2)李大婶购买这种商品5.5kg应付多少元？
解：(1)由表格观察到质量每增加1kg，售价就增加2.4元，所以此函数的表达式为y=2.4x.图象如图所示：
(2)购买这种商品5.5kg，即当x=5.5时，y=2.4×5.5=13.2，所以应付13.2元.