2022-2023学年浙江省温州市八年级上册数学期末专项突破模拟卷（卷一卷二）含解析

这是一份2022-2023学年浙江省温州市八年级上册数学期末专项突破模拟卷（卷一卷二）含解析，共52页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。

2022-2023学年浙江省温州市八年级上册数学期末专项突破模拟卷（卷一）
一、选一选（每小题3分，共30分）
1. 下列各组数中，能够作为直角三角形的三边长的一组是（　　）
A. 1，2，3 B. 2，3，4 C. 4，5，6 D. 3，4，5
2. 在平面直角坐标中，点在（ ）
A. 象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 如果a＞b，那么下列各式中正确的是（　　）
A B. C. D.
4. 在中和中，已知，，增加下列条件后还没有能判定≌的是（ ）．
A. B. C. D.
5. 如图，小正方形边长表示，点相对点的位置表述正确的是（ ）．

A. 北偏西方向 B. 南偏东方向
C. 北偏西方向处 D. 南偏东方向处
6. 满足下列条件的没有是直角三角形的是（ ）．
A. ，， B.
C. D.
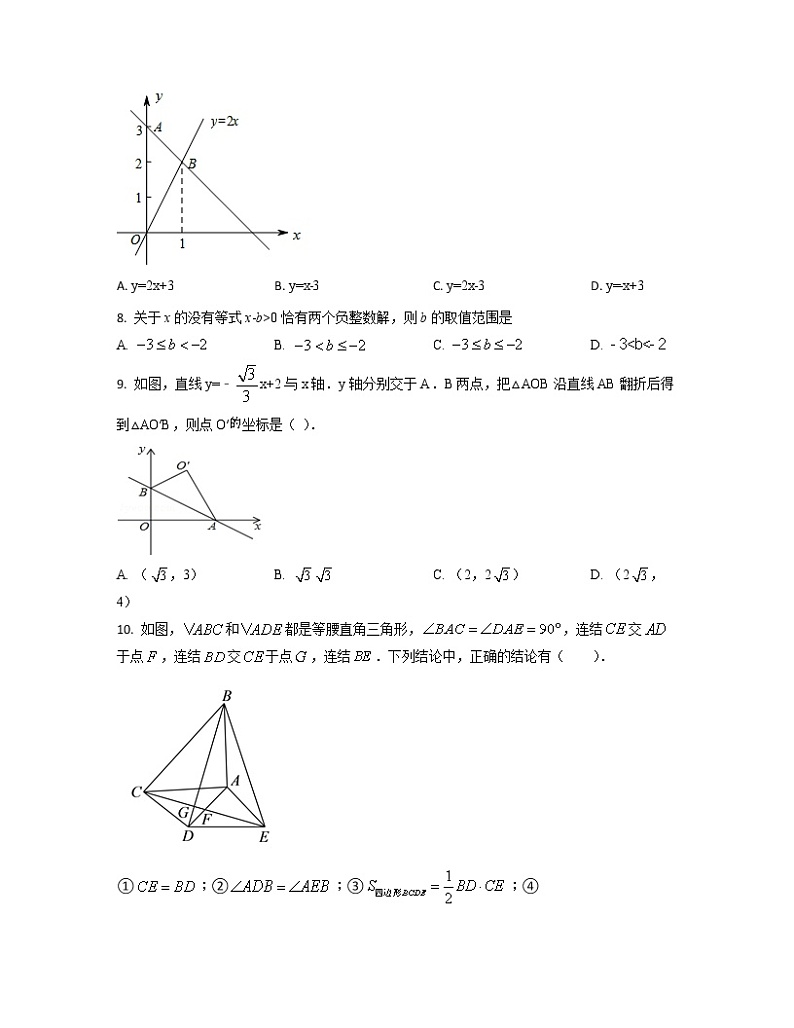
7. 如图，过A点的函数的图象与正比例函数y=2x的图象相交于点B，则这个函数的解析式是（　　）

A. y=2x+3 B. y=x﹣3 C. y=2x﹣3 D. y=﹣x+3
8. 关于x的没有等式x-b>0恰有两个负整数解，则b的取值范围是
A. B. C. D.
9. 如图，直线y=﹣x+2与x轴．y轴分别交于A．B两点，把△AOB沿直线AB翻折后得到△AO′B，则点O′坐标是（ ）．

A. （，3） B. C. （2，2） D. （2，4）
10. 如图，和都是等腰直角三角形，，连结交于点，连结交于点，连结．下列结论中，正确的结论有（ ）．

①；②；③；④
A. ①③ B. ①③④ C. ②③④ D. ①④
二、填 空 题（每小题4分，共24分）
11. 函数中的自变量的取值范围是__________．
12. 如图，在△ABC中，已知∠1=∠2，BE=CD，AB=5，AE=2，则CE=_____．

13. 已知点与点关于轴对称，则________，________．
14. 如图，中，，，分别为，的垂直平分线，如果，那么的周长为__________，__________．

15. 已知等腰三角形三边的长分别是，，，则它的周长是__________．
16. 甲、乙两车从地驶向地，甲车比乙车早行驶，并且在途中休息了，休息前后速度相同，如图是甲乙两车行驶的距离与时间的函数图象，当甲车行驶__________时，两车恰好相距．

三、解 答 题（共66分）
17. 如图，已知，，．求证：．

18. 解没有等式组，并把解集表示在数轴上．
19. 实验与操作：如图，中，，是的一个外角，根据要求进行尺规作图，并在图中表明相应的字母（保留作图痕迹，没有写作法）
（）作的平分线，作线段的垂直平分线，与交于点，与边交于点，连结．
（）猜测和的数量关系，并说明理由．

20. 已知：A（0，1），B（2，0），C（4，3）

（1）在坐标系中描出各点，画出△ABC；
（2）求△ABC的面积；
（3）设点P在y轴上，且△APB与△ABC的面积相等，求P的坐标．
21. 节约用水是我们美德，水龙头关闭没有严会造成滴水，容器内盛水与滴水时间的关系用可以显示水量的容器做如图的试验，并根据试验数据绘制出如图的函数图象，图象解答下列问题．
（）容器内原有水多少升．
（）求与之间的函数关系式，并计算在这种滴水状态下的滴水量是多少升．


22. 数学课上，林老师给出了下列方框中的一道题：
小聪和同桌小明讨论后，得出如下解答：
（）情况，探索结论
当点为的中点时，如图，确定线段与的大小关系，请你直接写出结论：______（填“”“”或“”）．
（）特例启发，解答问题
解：题目中，与的大小关系是__________（填“”“”或“”），理由如下：如图，过点作，交于点，（请你继续完成接下来的解题过程）．
（）拓展讨论，设计新题
①互换林老师所给题条件和结论，即：如图在等边三角形中，点在上，点在的延长线上，且，试确定线段与的大小关系，并说明理由．
②在等边三角形中，点在直线上，点在直线上，且，若的边长为，，求的长为__________（请你直接写出结果）．
如图，在等边三角形中，点在
上，点在的延长线上，且，
试确定线段与的大小关系，并说明理由．


23. 如图，已知等腰在平面直角坐标系中，顶点在轴上，直角顶点在轴上，点坐标为，直线的解析式为．
（）求直线的函数解析式．
（）如图，直线交轴于，延长至点，使，连结，求证：．
（）如图，直线交轴于，已知点的坐标为，在直线上是否存在一点，使的面积是面积的，若存在，请求出点的坐标；若没有存在，请说明理由．



2022-2023学年浙江省温州市八年级上册数学期末专项突破模拟卷（卷一）
一、选一选（每小题3分，共30分）
1. 下列各组数中，能够作为直角三角形的三边长的一组是（　　）
A. 1，2，3 B. 2，3，4 C. 4，5，6 D. 3，4，5
【正确答案】D

【分析】由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
【详解】A、12+22≠32，没有能构成直角三角形，故此选项没有符合题意；
B、22+32≠42，没有能构成直角三角形，故此选项没有符合题意；
C、42+52≠62，没有能构成直角三角形，故此选项没有符合题意；
D、32+42＝52，能构成直角三角形，故此选项符合题意．
故选：D．
本题考查勾股定理的逆定理，掌握勾股定理的逆定理是解题的关键．
2. 在平面直角坐标中，点在（ ）
A. 象限 B. 第二象限 C. 第三象限 D. 第四象限
【正确答案】B

【分析】横坐标小于0，纵坐标大于0，则这点在第二象限．
【详解】解：，，
在第二象限，
故选：B．
本题考查了点的坐标，解题的关键是掌握四个象限内坐标的符号：象限：，；第二象限：，；第三象限：，；第四象限：，．
3. 如果a＞b，那么下列各式中正确的是（　　）
A. B. C. D.
【正确答案】C

【分析】根据没有等式的基本性质对选项进行判断．
【详解】A、如果a＞b，根据没有等式的基本性质没有等式两边加（或减）同一个数（或式子），没有等号的方向没有变，a−3＜b没有成立；
B、没有等式两边乘（或除以）同一个正数，没有等号的方向没有变，没有成立；
C、没有等式两边乘（或除以）同一个负数，没有等号的方向改变，所以−2a＜−2b成立；
D、没有等式两边乘（或除以）同一个负数，没有等号的方向改变，所以−a>−b没有成立．
故选：C．
本题考查没有等式的基本性质，解题的关键是知道没有等式两边同时乘以或除以同一个数或式子时，一定要注意没有等号的方向是否改变．
4. 在中和中，已知，，增加下列条件后还没有能判定≌的是（ ）．
A. B. C. D.
【正确答案】C

【详解】若增加，则满足；
增加，满足；
增加，则，满足，
故选．
5. 如图，小正方形边长表示，点相对点的位置表述正确的是（ ）．

A. 北偏西方向 B. 南偏东方向
C. 北偏西方向处 D. 南偏东方向处
【正确答案】C

【详解】解：如图．∵∠ACB=90°，AC=2，BC=2，∴AB==，∠ABC=45°，
∴点在点的北偏西方向处．故选C．

6. 满足下列条件的没有是直角三角形的是（ ）．
A. ，， B.
C. D.
【正确答案】A

【详解】A、，，， ，∴此没有是直角三角形；
B、∵ ，∴此是直角三角形；
C、∵∠A+∠B+∠C=180°，∠A+∠B=∠C，∴∠C=90°，∴此是直角三角形；
D、∵∠A+∠B+∠C=180°，∠A：∠B：∠C=3：4：7，∴∠C=90°，∴此是直角三角形，
故选A.
7. 如图，过A点的函数的图象与正比例函数y=2x的图象相交于点B，则这个函数的解析式是（　　）

A y=2x+3 B. y=x﹣3 C. y=2x﹣3 D. y=﹣x+3
【正确答案】D

【详解】解：设函数解析式为：y=kx+b，

∵过点A的函数的图象过点A（0，3），与正比例函数y=2x的图象相交于点B（1，2），
∴可得出方程组，
解得，
则这个函数的解析式为y=﹣x+3．
故选：D．

8. 关于x的没有等式x-b>0恰有两个负整数解，则b的取值范围是
A. B. C. D.
【正确答案】A

【分析】根据题意可得没有等式恰好有两个负整数解，即-1和-2，再没有等式计算即可．
【详解】解：根据x的没有等式x-b>0恰有两个负整数解，可得x的负整数解为-1和-2


综合上述可得
故选A
本题主要考查没有等式的非整数解，关键在于非整数解的确定．
9. 如图，直线y=﹣x+2与x轴．y轴分别交于A．B两点，把△AOB沿直线AB翻折后得到△AO′B，则点O′的坐标是（ ）．

A. （，3） B. C. （2，2） D. （2，4）
【正确答案】A

【分析】作O′M⊥y轴，交y于点M，O′N⊥x轴，交x于点N，由直线y=﹣x+2与x轴、y轴分别交于A、B两点，求出A（0，2），B（2，0）和∠BAO=30°，运用直角三角形求出MB和MO′，再求出点O′的坐标．
【详解】如图，作O′M⊥y轴，交y于点M，O′N⊥x轴，交x于点N，

∵直线y=﹣x+2与x轴、y轴分别交于A、B两点，
∴A（0，2），B（2，0），
∴∠BAO=30°，
由折叠的特性得，O′B=OB=2，∠ABO=∠ABO′=60°，
∴MB=1，MO′=，
∴OM=3，ON=O′M=，
∴O′（，3），
故选：A．
【点题】本题主要考查了折叠问题及函数问题，解题的关键是运用折叠的特性得出相等的角与线段．
10. 如图，和都是等腰直角三角形，，连结交于点，连结交于点，连结．下列结论中，正确的结论有（ ）．

①；②；③；④
A. ①③ B. ①③④ C. ②③④ D. ①④
【正确答案】B

【详解】∵和都是等腰直角三角形，
∴，，
∵，
，
∴．
在和中，
，
∴≌，
∴，①正确；
∵≌，
∴，
∴，
在中，，
∴，
∴， ∴③正确；
在中，，
在中，，
∴．
在中，
，
中，
，
∴，
∴，故④正确；
∵≌，
∴，
∵与相等无法证明，
∴没有一定成立，故②错误；
故选．
本题考查了等腰三角形的性质、全等三角形的判定与性质、勾股定理的应用等，图形与已知选用恰当的方法与性质进行解答是关键.
二、填 空 题（每小题4分，共24分）
11. 函数中的自变量的取值范围是__________．
【正确答案】且

【详解】由题意得，解得：且，
故答案为且.
12. 如图，在△ABC中，已知∠1=∠2，BE=CD，AB=5，AE=2，则CE=_____．

【正确答案】3

【分析】由已知条件易证△ABE≌△ACD，再根据全等三角形的性质得出结论．
【详解】△ABE和△ACD中，
，
∴△ABE≌△ACD（AAS），
∴AD=AE=2，AC=AB=5，
∴CE=BD=AB﹣AD=3，
故答案为3．
13. 已知点与点关于轴对称，则________，________．
【正确答案】 ①. 3 ②. -4

【分析】根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”列方程求解即可．
【详解】∵点A（m-1，3）与点B（2，n+1）关于x轴对称，
∴m-1=2，n+1=-3，
解得m=3，n=-4．
故答案为3，-4．
本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：
（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数．
14. 如图，中，，，分别为，的垂直平分线，如果，那么的周长为__________，__________．

【正确答案】12，20．

【详解】∵为的垂直平分线，
∴，同理，
又，
设，
则∵为垂直平分线，
∴，
同理，
又，解得：，
∴，
故答案为12，20.
15. 已知等腰三角形三边的长分别是，，，则它的周长是__________．
【正确答案】12.3

【详解】若，则，
∴三边长分别为，，，没有能构成三角形；
若，则，
∴三边长分别为，，能构成三角形，周长为：；
若，则，
∴三边长分别为，，，没有构成三角形，
故答案为12.3.
16. 甲、乙两车从地驶向地，甲车比乙车早行驶，并且在途中休息了，休息前后速度相同，如图是甲乙两车行驶的距离与时间的函数图象，当甲车行驶__________时，两车恰好相距．

【正确答案】，，，

【详解】∵甲休息前后速度相同，
∴，∴，
，，
乙到达时间：；
设甲比乙快，乙还没出发，
∴；
设甲比乙快，乙已经出发，
则，解得，
设乙比甲快，且乙没到达，
则，解得，
设乙比甲快，且乙已经到达，
则，，
故答案为，，，.
本题考查了函数的应用，根据图象分情况进行讨论是解题的关键.
三、解 答 题（共66分）
17. 如图，已知，，．求证：．

【正确答案】证明见解析.

【详解】试题分析：证明≌，根据全等三角形的对应边相等即可得．
试题解析：∵，
∴，
∵，
∴，
∴，
∴≌，
∴．
18. 解没有等式组，并把解集表示在数轴上．
【正确答案】，数轴表示见解析.

【详解】解①得， ；
解②得， ；



19. 实验与操作：如图，中，，是的一个外角，根据要求进行尺规作图，并在图中表明相应的字母（保留作图痕迹，没有写作法）
（）作的平分线，作线段的垂直平分线，与交于点，与边交于点，连结．
（）猜测和的数量关系，并说明理由．

【正确答案】（）作图见解析；（），理由见解析.

【详解】试题分析：（1）直接利用角平分线的作法、线段垂直平分线的作法得出即可；
（2）利用全等三角形的判定得出△AEH≌△CEH（SAS），进而求出∠AEF=∠AFE，即可得出答案．
试题解析：
（）如图所示；

（），
设交于点，
∵为的角平分线，
∴，
∵是的一个外角，
∴，
又∵，
∴，
∴，
∴，
∵为的垂直平分线，
∴，
又∵，
∴≌，
∴，
又∵为的垂直平分线，
∴，
∴．
本题主要考查了复杂作图以及线段垂直平分线的性质与作法，正确把握线段垂直平分线的性质是解题关键．
20. 已知：A（0，1），B（2，0），C（4，3）

（1）在坐标系中描出各点，画出△ABC；
（2）求△ABC的面积；
（3）设点P在y轴上，且△APB与△ABC的面积相等，求P的坐标．
【正确答案】（1）图详见解析；（2）4；（3）点的坐标或

【分析】（1）确定出点、、的位置，连接、、即可；
（2）过点向、轴作垂线，垂足为、，△的面积四边形的面积-△ 的面积-△的面积-△的面积；
（3）当点在轴上时，根据△的面积可求，即可得出点的坐标．
【详解】解：（1）如图所示：

（2）过点向、轴作垂线，垂足为、．
四边形的面积，
△的面积，
△的面积，
△的面积．
△面积四边形的面积-△ 的面积-△的面积-△的面积；
∴．
（3）当点在轴上时，△的面积，即，解得：．
所以点的坐标为或．
本题主要考查的是点的坐标与图形的性质，明确△的面积四边形的面积-△的面积-△的面积-△的面积是解题的关键．
21. 节约用水是我们的美德，水龙头关闭没有严会造成滴水，容器内盛水与滴水时间的关系用可以显示水量的容器做如图的试验，并根据试验数据绘制出如图的函数图象，图象解答下列问题．
（）容器内原有水多少升．
（）求与之间的函数关系式，并计算在这种滴水状态下的滴水量是多少升．


【正确答案】（）容器的原有水升；（）滴水量为．

【分析】（1）由图象可知，当t=0时，w=0.3，即容器内原有水0.3升；
（2）设w与t之间的函数关系式为w=kt+b，将（0，0.3），（1.5，0.9）代入，即可求出w与t之间的函数关系式；由解析式可知，每小时滴水量为0.4L，的滴水量为：0.4×24=9.6L．
【详解】（1）根据图象可知，t=0时，w=0.3，即容器内原有水0.3升；

（2）设w与t之间的函数关系式为w=kt+b，将（0，0.3），（1.5，0.9）代入，得：，
解得：，
故w与t之间的函数关系式为w=0.4t+0.3；
由解析式可知，每小时滴水量为0.4L，的滴水量为：0.4×24=9.6L，
即在这种滴水状态下的滴水量是9.6升．

22. 数学课上，林老师给出了下列方框中的一道题：
小聪和同桌小明讨论后，得出如下解答：
（）情况，探索结论
当点为的中点时，如图，确定线段与的大小关系，请你直接写出结论：______（填“”“”或“”）．
（）特例启发，解答问题
解：题目中，与的大小关系是__________（填“”“”或“”），理由如下：如图，过点作，交于点，（请你继续完成接下来的解题过程）．
（）拓展讨论，设计新题
①互换林老师所给题的条件和结论，即：如图在等边三角形中，点在上，点在的延长线上，且，试确定线段与的大小关系，并说明理由．
②在等边三角形中，点在直线上，点在直线上，且，若的边长为，，求的长为__________（请你直接写出结果）．
如图，在等边三角形中，点在
上，点在的延长线上，且，
试确定线段与的大小关系，并说明理由．


【正确答案】（）；（），见解析；（）①；②或．

【详解】试题分析：（1）根据△ABC是等边三角形，点E为AB的中点，即可得出CE⊥AB，进而得出∠ECD=∠D，即可得出线段ED与EC的大小关系；
（2）首先得出BE=CF，进而利用△DBE≌△EFC即可得出答案；
（3）①作，交于点，可知等边三角形，进而证明≌，即可得出；
②分点D在CB的延长线上、在BC的延长线上两种情况进行讨论即可得.
试题解析：（）．
∵为等边三角形，是中点，∴，，．
∵，∴，
∴，∴，
∴，∴．
（）
在等边中，，
∴为等边三角形，
∴，
又∵，
∴，
又∵，
∴，
同理，
又在中，，
在中，，
∴，
在和中，
，
∴≌，
∴．
（）①作，交于点，
则可知为等边三角形，
∴．
又∵，
∴，
又∵，
∴，
又∵在中，，
在中，，
∴，
∴和中，
，
∴≌，
∴，
∴．
②，
∴或．
23. 如图，已知等腰在平面直角坐标系中，顶点在轴上，直角顶点在轴上，点的坐标为，直线的解析式为．
（）求直线的函数解析式．
（）如图，直线交轴于，延长至点，使，连结，求证：．
（）如图，直线交轴于，已知点的坐标为，在直线上是否存在一点，使的面积是面积的，若存在，请求出点的坐标；若没有存在，请说明理由．

【正确答案】（）；（）证明见解析；（）或．

【详解】试题分析：（1）先求出A点坐标，再根据点C坐标求出AC的长，再根据等腰求出AB的长，再根据勾股定理求得BO的长，确定点B的坐标，再利用待定系数法即可求得；
（2）根据已知确定点D的坐标，然后求出AD的长，由（1）已知AC的长，比较即可得；
（3）先求出的面积，然后分点P在x轴上方与下文两种情况根据的面积是面积的，列式进行计算即可得.
试题解析：（）且顶点在轴上，
∴，
又∵，
∴，
∵是，
∴，
∴BO==1，
∵在轴负半轴上，
∴，
∴ ；
（）∵，，
∴，
∵．
∵，
∴，
∴，
又∵，
∴ ；
（）对 ，
令，，
∴，
∴ ，
设，
又∵，
∴ ，
此时 ，
∴ ，
又∵，
∴ ，
∴，
∴．
若 ，
∴，
则，
又∵，
∴，
，
∴．
综上或．
本题考查函数综合题，涉及到待定系数法，勾股定理、等腰直角三角形的性质等，已知与图形选择适合的方法与性质是解题的关键.



























2022-2023学年浙江省温州市八年级上册数学期末专项突破模拟卷（卷二）
一、选一选（本大题共30分，每小题3分）
1. 低碳环保理念深入人心，共享单车已成为出行新方式下列共享单车图标（没有考虑外围方框），是轴对称图形是　　
A. B. C. D.
2. 下列计算正确的是（ ）
A. B. C. D.
3. 叶绿体是植物进行光合作用的场所，叶绿体DNA最先发现于衣藻叶绿体，长约0.00005米．其中，0.00005用科学记数法表示为（　　）
A. 0.5×10﹣4 B. 5×10﹣4 C. 5×10﹣5 D. 50×10﹣3
4. 若分式的值等于0，则的值为（ ）
A. B. 1 C. D. 2
5. 如图，点D、E在△ABC的边BC上，△ABD≌△ACE，下列结论没有一定成立的是（ ）

A. B. C. D.
6. 已知等腰三角形一个角为70°，则底角为（ ）
A. 70° B. 40° C. 70°或55° D. 40°或70°
7. 已知可以写成一个完全平方式，则可为( )
A. 4 B. 8 C. 16 D.
8. 在平面直角坐标系xOy中，以原点O为圆心，任意长为半径作弧，分别交x轴负半轴和y轴的正半轴于A点，B点．分别以点A，点B为圆心，AB的长为半径作弧，两弧交于P点．若点P的坐标为（a，b），则（ ）
A. B. C. D.
9. 若，则的值为（ ）
A. 3 B. 6 C. 9 D. 12
10. 某小区有一块边长为a的正方形场地，修建两条宽为b的绿化带. 一如图甲所示，绿化带面积为S甲：二如图乙所示，绿化带面积为S乙. 设，下列选项中正确的是（ ）

A. B. C. D.
二、填 空 题（本大题共24分，每小题3分）
11. 如图，在四边形ABCD中，∠A=90°，∠D=40°，则∠B+∠C为__________．

12. 已知点P（3，﹣1）关于y轴对称点Q的坐标是_____________.
13. 已知分式满足条件“只含有字母x，且当x＝1时无意义”，请写出一个这样的分式：_____．
14. 已知△ABC中，AB=2，∠C=40°，请你添加一个适当的条件，使△ABC的形状和大小都是确定的．你添加的条件是________________．
15. 某地过后，小娜同学用下面的方法检测教室的房梁是否处于水平：在等腰直角三角尺斜边中点O处拴一条线绳，线绳的另一端挂一个铅锤，把这块三角尺的斜边贴在房梁上，结果线绳三角尺的直角顶点，由此得出房梁是水平的即挂铅锤的线绳与房梁直），用到的数学原理是_____．

16. 如图，在平面直角坐标系xOy中，△DEF可以看作是△ABC若干次的图形变化（轴对称、平移）得到的，写出一种由△ABC得到△DEF的过程：____________．

17. 如图．在中，，，和的平分线交于点，过点作的平行线交于点，交于点，则的周长为_________．


18. 已知一张三角形纸片ABC（如图甲），其中∠ABC=∠C．将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为BD（如图乙）．再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为EF（如图丙）．原三角形纸片ABC中，∠ABC的大小为______°．

三、解 答 题（本大题共17分，第19题8分， 第20题4分，第21题5分）
19. 计算：（1）；
（2）．
20. 如图，，，，是同一条直线上的点，，，．求证：．

21. 解方程：．
四、解 答 题（本大题共15分，每小题5分）
22. 先化简，再求值：，其中．
23. 如图，A，B分别为CD，CE中点，AE⊥CD于点A，BD⊥CE于点B．求∠AEC的度数．

24. 列方程解应用题：
中华传统文化是中华民族的“根”和“魂”，是我们必须世代传承的文化根脉、文化基因.为传承传统文化，某校为各班购进《三国演义》和《水浒传》连环画若干套，其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元，用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍，求每套《水浒传》连环画的价格．
五、解 答 题（本大题共14分，第25、26题各7分）
25. 阅读材料
小明遇到这样一个问题：求计算所得多项式的项系数．
小明想通过计算所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法．
他决定从简单情况开始，先找所得多项式中的项系数．通过观察发现：

也就是说，只需用x+2中的项系数1乘以2x+3中的常数项3，再用x+2中的常数项2乘以2x+3中的项系数2，两个积相加1×3+2×2=7，即可得到项系数．
延续上面的方法，求计算所得多项式的项系数．可以先用x+2的项系数1，2x+3的常数项3，3x+4的常数项4，相乘得到12；再用2x+3的项系数2，x+2的常数项2，3x+4的常数项4，相乘得到16；然后用3x+4的项系数3，x+2的常数项2，2x+3的常数项3，相乘得到18．将12，16，18相加，得到的项系数为46．
参考小明思考问题的方法，解决下列问题：
（1）计算（2x+1）（3x+2）所得多项式的项系数为　 　．
（2）计算（x+1）（3x+2）（4x﹣3）所得多项式的项系数为　 　．
（3）若计算（x2+x+1）（x2﹣3x+a）（2x﹣1）所得多项式的项系数为0，则a=　 　．
（4）若x2﹣3x+1是x4+ax2+bx+2的一个因式，则2a+b的值为　 　．
26. 如图，CN是等边的外角内部的一条射线，点A关于CN的对称点为D，连接AD，BD，CD，其中AD，BD分别交射线CN于点E，P．


（1）依题意补全图形；
（2）若，直接写出的大小__________（用含的式子表示）；
（3）用等式表示线段PB，PC与PE之间的数量关系，并证明.（第（2）问中的结论可以直接使用）
附加题：（本题10分，可计入总分，但全卷总分没有超过100分）
27. 对于0，1以及真分数p，q，r，若p

两个没有等的正分数有无数多个中间分数．例如：上表中第③行中的3个分数、、，有，所以为和的一个中间分数，在表中还可以找到和的中间分数，，，．把这个表一直写下去，可以找到和更多的中间分数．
（1）按上表的排列规律，完成下面的填空：
①上表中括号内应填的数为 ；
②如果把上面的表一直写下去，那么表中个出现的和的中间分数是 ；
（2）写出分数和（a、b、c、d均为正整数，，）的一个中间分数（用含a、b、c、d的式子表示），并证明；
（3）若与（m、n、s、 t均为正整数）都是和的中间分数，则的最小值为 ．







2022-2023学年浙江省温州市八年级上册数学期末专项突破模拟卷（卷二）
一、选一选（本大题共30分，每小题3分）
1. 低碳环保理念深入人心，共享单车已成为出行新方式下列共享单车图标（没有考虑外围方框），是轴对称图形的是　　
A. B. C. D.
【正确答案】A

【分析】根据轴对称图形的定义判断.
【详解】A是轴对称图形，故符合题意；B没有是轴对称图形，故没有符合题意；C没有是轴对称图形，故没有符合题意；D没有是轴对称图形，故没有符合题意，
故选A.
本题考查判断轴对称图形，关键是找到对称轴.
2. 下列计算正确的是（ ）
A. B. C. D.
【正确答案】BC

【分析】A选项：没有是同类项，故没有能合并；
B选项：同底数幂相乘，底数没有变，指数相加；
C选项：幂的乘方，底数没有变，指数相乘；
D选项：同底数幂相除，底数没有变，指数相减；
【详解】A选项：没有是同类项，没有能合并，故是错误的；
B选项：，故是正确；
C选项：，故是正确的；
D选项：，故是错误的；
故选BC.
考查了同底数幂的乘、除法和幂的乘方的运算，解题关键是牢记运算法则：①同底数幂相乘，底数没有变，指数相加；②幂的乘方，底数没有变，指数相乘；③同底数幂相除，底数没有变，指数相减.
3. 叶绿体是植物进行光合作用的场所，叶绿体DNA最先发现于衣藻叶绿体，长约0.00005米．其中，0.00005用科学记数法表示为（　　）
A. 0.5×10﹣4 B. 5×10﹣4 C. 5×10﹣5 D. 50×10﹣3
【正确答案】C

【详解】值小于1的负数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法没有同的是其所使用的是负指数幂，指数由原数左边起个没有为零的数字前面的0的个数所决定，
0.00005＝，
故选：C.
4. 若分式的值等于0，则的值为（ ）
A. B. 1 C. D. 2
【正确答案】A

【详解】由题意得：ａ+1=0且a≠0，解得：a=-1，
故选A.
本题考查了分式值为0的条件，解题的关键是要熟记分式值为0时，分子为0且分母没有为0.
5. 如图，点D、E在△ABC的边BC上，△ABD≌△ACE，下列结论没有一定成立的是（ ）

A. B. C. D.
【正确答案】A

【分析】根据全等三角形的对应边相等、对应角相等逐一判断即可．
【详解】∵△ABD≌△ACE，
∴BD=CE，
∴BE=CD，
故B成立，没有符合题意；
∠ADB=∠AEC，
∴∠ADE=∠AED，
故C成立，没有符合题意；
∠BAD=∠CAE，
∴∠BAE=∠CAD，
故D成立，没有符合题意；
AC没有一定等于CD，
故A没有成立，符合题意．
故选：A．
本题考查的是全等三角形的性质，掌握全等三角形的对应边相等、对应角相等是解题的关键．
6. 已知等腰三角形的一个角为70°，则底角为（ ）
A. 70° B. 40° C. 70°或55° D. 40°或70°
【正确答案】C

【分析】题中未指明已知的角是顶角还是底角，故应该分情况进行分析，从而求解．
【详解】解：①当这个角是顶角时，底角=（180°-70°）÷2=55°；
②当这个角是底角时，另一个底角为70°，因为70°+70°＜180°，符合三角形内角和定理；
故选C．
本题考查等腰三角形的性质及三角形内角和定理的综合运用，解题的关键是能够进行分类讨论．
7. 已知可以写成一个完全平方式，则可为( )
A. 4 B. 8 C. 16 D.
【正确答案】C

【详解】∵可以写成一个完全平方式，
∴x2-8x+a=(x-4)2，
又（x-4）2=x2-8x+16，
∴a=16，
故选C．
8. 在平面直角坐标系xOy中，以原点O为圆心，任意长为半径作弧，分别交x轴的负半轴和y轴的正半轴于A点，B点．分别以点A，点B为圆心，AB的长为半径作弧，两弧交于P点．若点P的坐标为（a，b），则（ ）
A. B. C. D.
【正确答案】D

【详解】根据题意可知OP是第二象限坐标轴夹角的平分线，所以a=-b，
故选：D.

9. 若，则的值为（ ）
A. 3 B. 6 C. 9 D. 12
【正确答案】C

【详解】∵a+b=3，
∴a2-b2+6b
=(a+b)(a-b)+6b
=3(a-b)+6b
=3a-3b+6b
=3a+3b
=3(a+b)
=9．
故选C
10. 某小区有一块边长为a的正方形场地，修建两条宽为b的绿化带. 一如图甲所示，绿化带面积为S甲：二如图乙所示，绿化带面积为S乙. 设，下列选项中正确的是（ ）

A. B. C. D.
【正确答案】D

【分析】由题意可求S甲=2ab-b2，S乙=2ab，代入可求k的取值范围．
【详解】∵S甲=2ab-b2，S乙=2ab．
∴
∵a＞b＞0
∴＜k＜1
故选D．
本题考查了正方形的性质，能用代数式正确表示阴影部分面积是本题的关键．
二、填 空 题（本大题共24分，每小题3分）
11. 如图，在四边形ABCD中，∠A=90°，∠D=40°，则∠B+∠C为__________．

【正确答案】230°

【分析】

【详解】∵∠A+∠B+∠C+∠D=（4-2）×180°=360°，∠A=90°，∠D=40°，∴∠B+∠C=360°-90°-40°=230°，
故答案为230°.
本题考查了四边形的内角和，熟记四边形的内角和是360度是解题的关键.
12. 已知点P（3，﹣1）关于y轴的对称点Q的坐标是_____________.
【正确答案】（-3，-1）

【分析】根据关于y轴对称的点的坐标为，纵坐标没有变，横坐标互为相反数即可解答.
【详解】解：∵点Q与点P（3，﹣1）关于y轴对称，
∴Q（-3，-1）.
故答案为（-3，-1）.
本题主要考查关于对称轴对称的点的坐标特征，解此题的关键在于熟练掌握其知识点.
13. 已知分式满足条件“只含有字母x，且当x＝1时无意义”，请写出一个这样的分式：_____．
【正确答案】

【详解】由分式满足条件“只含有字母x，且当x=1时无意义”，可知分式的分母中含有因式x-1，
所以这样的分式可以是（答案没有），
故答案为.
14. 已知△ABC中，AB=2，∠C=40°，请你添加一个适当的条件，使△ABC的形状和大小都是确定的．你添加的条件是________________．
【正确答案】∠A=60°(答案没有)

【详解】已知一边和这条边的对角，要想确定的三角形，可以再添加一个角，根据AAS或ASA即可确定三角形，如添加：∠A=60°，
故答案为答案没有，如：∠A=60°.
15. 某地过后，小娜同学用下面的方法检测教室的房梁是否处于水平：在等腰直角三角尺斜边中点O处拴一条线绳，线绳的另一端挂一个铅锤，把这块三角尺的斜边贴在房梁上，结果线绳三角尺的直角顶点，由此得出房梁是水平的即挂铅锤的线绳与房梁直），用到的数学原理是_____．

【正确答案】等腰三角形的底边上的中线、底边上的高重合

【分析】根据△ABC是个等腰三角形可得AC＝BC，再根据点O是AB的中点，即可得出OC⊥AB，然后即可得出结论．
【详解】解：∵△ABC是个等腰三角形，
∴AC＝BC，
∵点O是AB的中点，
∴AO＝BO，
∴OC⊥AB．
故等腰三角形的底边上的中线、底边上的高重合．
本题考查了学生对等腰三角形的性质的理解和掌握,此题与实际生活联系密切,体现了从数学走向生活的指导思想,从而达到学以致用的目的.
16. 如图，在平面直角坐标系xOy中，△DEF可以看作是△ABC若干次的图形变化（轴对称、平移）得到的，写出一种由△ABC得到△DEF的过程：____________．

【正确答案】答案没有，如：将△ABC关于y轴对称，再将三角形向上平移3个单位长度

详解】将△ABC关于y轴对称，再将三角形向上平移3个单位长度得到△DEF；
或：将△ABC向上平移3个单位长度，再关于y轴对称得到△DEF，
故答案为答案没有，如：将△ABC关于y轴对称，再将三角形向上平移3个单位长度得到△DEF.
17. 如图．在中，，，和的平分线交于点，过点作的平行线交于点，交于点，则的周长为_________．


【正确答案】10

【分析】利用角平分线及平行线性质，等腰三角形的判定得到MB＝MO，NC＝NO，将三角形AMN周长转化，求出即可．
【详解】解：∵BO为∠ABC的平分线，CO为∠ACB的平分线，
∴∠ABO＝∠CBO，∠ACO＝∠BCO，
∵MN∥BC，
∴∠MOB＝∠OBC，∠NOC＝∠BCO，
∴∠ABO＝∠MOB，∠NOC＝∠ACO，
∴MB＝MO，NC＝NO，
∴MN＝MO＋NO＝MB＋NC，
∵AB＝4，AC＝6，
∴△AMN周长为AM＋MN＋AN＝AM＋MB＋AN＋NC＝AB＋AC＝10，
故答案10
此题考查了等腰三角形的判定，以及平行线的性质，熟练掌握等腰三角形的判定和平行线的性质是解题的关键．
18. 已知一张三角形纸片ABC（如图甲），其中∠ABC=∠C．将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为BD（如图乙）．再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为EF（如图丙）．原三角形纸片ABC中，∠ABC的大小为______°．

【正确答案】72°．

【分析】根据题意设∠A为x，再根据翻折性质得到∠C=∠BED=2x，再根据AB=AC，得出∠ABC=∠C=2x，然后根据三角形内角和列出方程2x+2x+x=180°，解方程即可．
【详解】解：设∠A为x，
则翻折点A恰好与点D重合，折痕为EF由对应角相等可得∠EDA=∠A=x，
由∠BED是△AED的外角可得∠BED=∠EDA+∠A=2x，
则翻折点C落到AB边上的E点处，折痕为BD由对应角相等可得∠C=∠BED=2x，
∵AB=AC，
∴∠ABC=∠C=2x，
在△ABC中，∠ABC+∠C+∠A=2x+2x+x=180°，
∴x=36°，
∴∠ABC=2x=72°．
故答案为72°．

本题主要考查折叠性质，三角形外角性质．三角形内角和定理和等腰三角形的性质，解一元方程，掌握三角形内角和定理和等腰三角形的性质，折叠性质，解一元方程，三角形外角性质是解题关键．
三、解 答 题（本大题共17分，第19题8分， 第20题4分，第21题5分）
19. 计算：（1）；
（2）．
【正确答案】（1）（2）3x-2y

【详解】试题分析：（1）先分别计算值、算术平方根、负指数幂、0次幂，然后再按运算顺序进行计算即可；
（2）先将被除式因式分解，再将除式利用除法法则进行颠倒，然后再相乘即可.
试题解析：（1）原式==；
（2）原式===．
20. 如图，，，，是同一条直线上的点，，，．求证：．

【正确答案】见解析

【分析】根据等式的性质得出，再利用证明．
【详解】证明：，，，
，
，
，
在和中，
，
，
．
考查了全等三角形的判定与性质以及平行线的性质，利用全等三角形的判定定理证出是解题的关键．
21. 解方程：．
【正确答案】x=

【详解】试题分析:两边都乘最简公分母，没有要漏乘左边没有分母的项，把分式方程化为整式方程,求出x的值，然后检验.
解：方程两边乘，得
．
解得．
检验：当时，．
∴原分式方程的解为．
点睛：本题考查了分式方程的解法,解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解，解分式方程一定要注意验根.
四、解 答 题（本大题共15分，每小题5分）
22. 先化简，再求值：，其中．
【正确答案】m2+2m ；15

【详解】试题分析：括号内先通分进行加减运算，然后再进行除法运算，代入数值进行计算即可.
试题解析：原式====，
当时，原式=15．
23. 如图，A，B分别为CD，CE的中点，AE⊥CD于点A，BD⊥CE于点B．求∠AEC的度数．

【正确答案】30°

【分析】试题分析：连接DE，由A，B分别为CD，CE的中点，AE⊥CD于点A，BD⊥CE于点B可证明得到△CDE为等边三角形，再利用直角三角形两锐角互余即可得.
【详解】试题解析：连接DE，
∵A，B分别为CD，CE的中点，
AE⊥CD于点A，BD⊥CE于点B，
∴CD＝CE＝DE，
∴△CDE为等边三角形，
∴∠C＝60°，
∴∠AEC＝90°－∠C＝30°．

24. 列方程解应用题：
中华传统文化是中华民族的“根”和“魂”，是我们必须世代传承的文化根脉、文化基因.为传承传统文化，某校为各班购进《三国演义》和《水浒传》连环画若干套，其中每套《三国演义》连环画的价格比每套《水浒传》连环画的价格贵60元，用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍，求每套《水浒传》连环画的价格．
【正确答案】每套《水浒传》连环画的价格为120元

【分析】设每套《水浒传》连环画的价格为x元，则每套《三国演义》连环画的价格为(x+60)元，根据等量关系“用4800元购买《水浒传》连环画的套数是用3600元购买《三国演义》连环画套数的2倍”列方程进行求解即可得.
【详解】设每套《水浒传》连环画的价格为元，则每套《三国演义》连环画的价格为元，由题意，
得，
解得，
经检验，是原方程的解，且符合题意，
答：每套《水浒传》连环画的价格为120元．
本题考查了分式方程的应用，找到题中的等量关系是解题的关键，注意解完方程后要进行检验.
五、解 答 题（本大题共14分，第25、26题各7分）
25. 阅读材料
小明遇到这样一个问题：求计算所得多项式的项系数．
小明想通过计算所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法．
他决定从简单情况开始，先找所得多项式中的项系数．通过观察发现：

也就是说，只需用x+2中的项系数1乘以2x+3中的常数项3，再用x+2中的常数项2乘以2x+3中的项系数2，两个积相加1×3+2×2=7，即可得到项系数．
延续上面的方法，求计算所得多项式的项系数．可以先用x+2的项系数1，2x+3的常数项3，3x+4的常数项4，相乘得到12；再用2x+3的项系数2，x+2的常数项2，3x+4的常数项4，相乘得到16；然后用3x+4的项系数3，x+2的常数项2，2x+3的常数项3，相乘得到18．将12，16，18相加，得到的项系数为46．
参考小明思考问题的方法，解决下列问题：
（1）计算（2x+1）（3x+2）所得多项式的项系数为　 　．
（2）计算（x+1）（3x+2）（4x﹣3）所得多项式的项系数为　 　．
（3）若计算（x2+x+1）（x2﹣3x+a）（2x﹣1）所得多项式的项系数为0，则a=　 　．
（4）若x2﹣3x+1是x4+ax2+bx+2的一个因式，则2a+b的值为　 　．
【正确答案】（1）7（2）-7（3）-3（4）-15

【分析】（1）用2x+1中的项系数2乘以3x+2中的常数项2得4，用2x+1中的常数项1乘以3x+2中的项系数3得3，4+3=7即为积中项的系数；
（2）用x+1中的项系数1，3x+2中的常数项2，4x-3中的常数项-3相乘得-6，用x+1中的常数项1，3x+2中的项系数3，4x-3中的常数项-3相乘得-9，用x+1中的常数项1，3x+2中的常数项2，4x-3中的项系数4相乘得8，-6-9+8=-7即为积中项系数；
（3）用每一个因式中的项系数与另两个因式中的常数项相乘，再把所得的积相加，列方程、解方程即可得；
（4）设可以分成（ ）(x2+kx+2)，根据小明的算法则有k-3=0，a=-3k+2+1，b=-3×2+k，解方程即可得.
【详解】解：（1）2×2+1×3=7，
故7；
（2）1×2×（-3）+3×1×（-3）+4×1×2=，
故；
（3）由题意得：，解得：，
故；
（4）设可以分成（ ），
则有
解得：，
所以，
故 .
26. 如图，CN是等边的外角内部的一条射线，点A关于CN的对称点为D，连接AD，BD，CD，其中AD，BD分别交射线CN于点E，P．


（1）依题意补全图形；
（2）若，直接写出的大小__________（用含的式子表示）；
（3）用等式表示线段PB，PC与PE之间的数量关系，并证明.（第（2）问中的结论可以直接使用）
【正确答案】（1）作图见解析；（2）；（3），证明见解析

【分析】（1）根据题意作图即可；
（2）根据等边三角形的性质求解即可；
（3）在PB上截取PF使，连接CF，证明是等边三角形，在证明即可得解；
【详解】（1）根据题意作图如下：


（2）∵点A与点D关于CN对称，
∴CN是AD的垂直平分线，
∴，
∵，
∴，
∵是等边三角形，
∴，，
∴，
∴；
故答案是：；
（3），证明过程如下：
PB上截取PF使，连接CF，


∵，，
∴，
∵，
∴，
∴，
∵，
∴等边三角形，
∴，
∴，
∴在和中，
，
∴，
∴，
∴．
本题主要考查了全等三角形的判定与性质，轴对称作图，等边三角形的判定与性质，准确分析证明是解题的关键．
附加题：（本题10分，可计入总分，但全卷总分没有超过100分）
27. 对于0，1以及真分数p，q，r，若p

两个没有等的正分数有无数多个中间分数．例如：上表中第③行中的3个分数、、，有，所以为和的一个中间分数，在表中还可以找到和的中间分数，，，．把这个表一直写下去，可以找到和更多的中间分数．
（1）按上表的排列规律，完成下面的填空：
①上表中括号内应填的数为 ；
②如果把上面的表一直写下去，那么表中个出现的和的中间分数是 ；
（2）写出分数和（a、b、c、d均为正整数，，）的一个中间分数（用含a、b、c、d的式子表示），并证明；
（3）若与（m、n、s、 t均为正整数）都是和的中间分数，则的最小值为 ．
【正确答案】（1）①；②（2）证明见解析（3）1504

【详解】试题分析：（1）①观察每一行的规律可得括号位于第⑦行，按表格中的规律可知是；
②观察表格可知个出现的和的中间分数在第⑧行，是；
（2）答案没有，根据表格中观察到的，可以为，通过推导证明即可得；
（3）根据排列可知和的中间分数有，，，等，由此可得.
试题解析：（1）①观察每一行的规律可得括号位于第⑦行，按分子的排序可知是，
②观察表格可知个出现的和的中间分数在第⑧行，是，
故答案为①；②．
（2）本题结论没有，证法没有，如：
结论：．
∵a、b、c、d均为正整数，，，
∴，
．
∴．
（3）根据排列可知和的中间分数有，，，等，由此可得mn的最小值为1504，
故答案为1504.
本题考查了规律性问题，第（1）问题相对来说比较容易，后面两问需要通过分析发现其中存在的关系，然后用来解题，比较抽象，需要有一定的想象力.