2022-2023学年辽宁省鞍山市八年级上册数学期末专项提升模拟卷（AB卷）含解析

这是一份2022-2023学年辽宁省鞍山市八年级上册数学期末专项提升模拟卷（AB卷）含解析，共39页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。
2022-2023学年辽宁省鞍山市八年级上册数学期末专项提升模拟卷（A卷）
一、选一选（共12小题，每小题4分，共48分）
1. 第24届冬季，将于2022年02月04日～2022年02月20日在北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中没有是轴对称图形的是（　　）
A. B. C. D.
2. 下列线段，能组成三角形的是（ ）
A. 2cm,3cm,5cm B. 5cm,6cm,10cm C. 1cm,1cm,3cm D. 3cm,4cm,8cm
3. 在一个三角形中，一个外角是其相邻内角的3倍，那么这个外角是（ ）
A. 150° B. 135° C. 120° D. 100°
4. 下列运算结果正确的是（ ）
A. B. C. D.
5. 若分式有意义,则a的取值范围是(     )
A. a≠2 B. a≠0 C. a≠2且a≠0 D. 一切实数
6. 若,则A(     )
A. 2ab B. -2ab C. 4ab D. -4ab
7. 下列各式能用平方差公式分解因式的有( )
①x2+y2；②x2﹣y2；③﹣x2﹣y2；④﹣x2+y2；⑤﹣x2+2xy﹣y2．
A. 4个 B. 3个 C. 2个 D. 1个
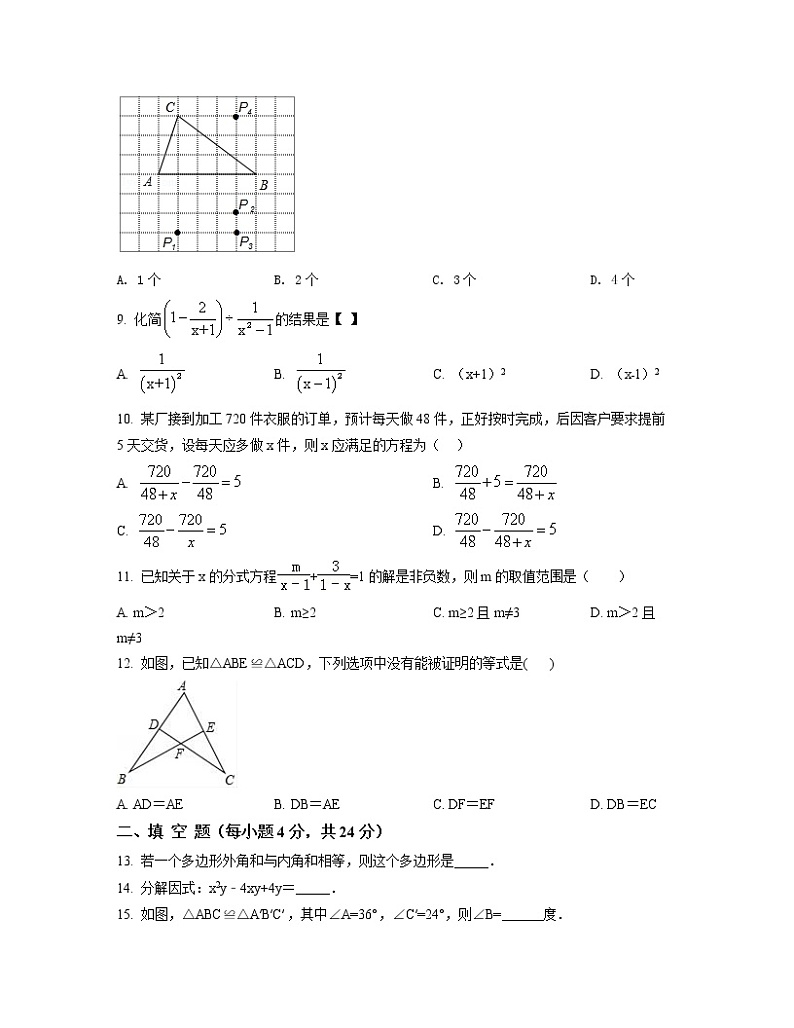
8. 如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（ ）

A. 1个 B. 2个 C. 3个 D. 4个
9. 化简的结果是【 】
A. B. C. （x+1）2 D. （x﹣1）2
10. 某厂接到加工720件衣服的订单，预计每天做48件，正好按时完成，后因客户要求提前5天交货，设每天应多做x件，则x应满足的方程为（ ）
A. B.
C. D.
11. 已知关于x的分式方程+=1的解是非负数，则m的取值范围是（　　）
A. m＞2 B. m≥2 C. m≥2且m≠3 D. m＞2且m≠3
12. 如图，已知△ABE≌△ACD，下列选项中没有能被证明的等式是( )

A. AD＝AE B. DB＝AE C. DF＝EF D. DB＝EC
二、填 空 题（每小题4分，共24分）
13. 若一个多边形外角和与内角和相等，则这个多边形是_____．
14. 分解因式：x2y﹣4xy+4y＝_____．
15. 如图，△ABC≌△A′B′C′，其中∠A=36°，∠C′=24°，则∠B=______度．

16. 已知4y2+my+1是完全平方式，则常数m值是______．
17. 如图，点P是∠AOB内部一点，∠AOB=30°，OP=8cm，M，N是OA，OB上的两个动点，则△MPN周长的最小值_____cm．

18. 若分式方程无解,则k=__________
三、解 答 题：（简答题要写出必要的解题步骤和证明过程，共78分）
19. （1）分解因式：① ， ②；
（2）已知a+b=2,求的值.
20. 已知，如图 ，在△ABC中，∠C=∠ABC=2∠A，BD是AC边上的高，求∠DBC的度数

21. 如图,点A、D、E在直线l上,∠BAC=90°,AB=AC,BD⊥l于D,CE⊥l于E,求证:DE=BD+CE.

22. 如图，已知Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC平分线分别交BC、CD于E、F.试说明△CEF是等腰三角形.

23. 如图,在平面直角坐标系中,A(-1，5)，B（-1，0），C（-4，3）.

（1）在图中作出△ABC关于y轴的对称图形△A1B1C1；
（2）写出点A1、B1、C1的坐标；
（3）在y轴上画出点P，使PA+PC最小；  
（4）求六边形AA1C1B1BC的面积．.
24. 甲、乙、丙三个登山爱好者经常相约去登山，今年1月甲参加了两次登山．
（1）1月1日甲与乙同时开始攀登一座900米高的山，甲的平均攀登速度是乙的1.2倍，结果甲比乙早15分钟到达顶峰．求甲的平均攀登速度是每分钟多少米？
（2）1月6日甲与丙去攀登另一座h米高的山，甲保持第（1）问中的速度没有变，比丙晚出发0.5小时，结果两人同时到达顶峰，问甲的平均攀登速度是丙的多少倍？（用含h的代数式表示）
25. 已知∠MAN=120°，点C是∠MAN的平分线AQ上的一个定点，点B，D分别在AN，AM上，连接BD．
【发现】
（1）如图1，若∠ABC=∠ADC=90°，则∠BCD=　 　°，△CBD是　 　三角形；
【探索】
（2）如图2，若∠ABC+∠ADC=180°，请判断△CBD形状，并证明你的结论；
【应用】
（3）如图3，已知∠EOF=120°，OP平分∠EOF，且OP=1，若点G，H分别在射线OE，OF上，且△PGH为等边三角形，则满足上述条件的△PGH的个数一共有　 　．（只填序号）
①2个 ②3个 ③4个 ④4个以上

























2022-2023学年辽宁省鞍山市八年级上册数学期末专项提升模拟卷（A卷）
一、选一选（共12小题，每小题4分，共48分）
1. 第24届冬季，将于2022年02月04日～2022年02月20日在北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中没有是轴对称图形的是（　　）
A B. C. D.
【正确答案】D

【详解】A、是轴对称图形，故此选项没有符合题意；
B、是轴对称图形，故此选项没有符合题意；
C、是轴对称图形，故此选项没有符合题意；
D、没有是轴对称图形，故此选项符合题意；
故选D．
2. 下列线段，能组成三角形的是（ ）
A. 2cm,3cm,5cm B. 5cm,6cm,10cm C. 1cm,1cm,3cm D. 3cm,4cm,8cm
【正确答案】B

【分析】根据三角形的三边关系定理即可进行判断．
【详解】解：A、3+2=5，故选项错误；
B、5+6＞10，故正确；
C、1+1＜3，故错误；
D、4+3＜8，故错误．
故选B．
考查了三角形的三边关系，验证三角形的三边关系定理：任意两边之和大于第三边．只要验证两条较短的边的和大于最长的边即可．
3. 在一个三角形中，一个外角是其相邻内角的3倍，那么这个外角是（ ）
A. 150° B. 135° C. 120° D. 100°
【正确答案】B

【详解】由题意可知，可设内角为α，则外角为3α，
∴α+3α=180°，
∴α=45°，
则外角为3α=135°，
故选B.
4. 下列运算结果正确的是（ ）
A. B. C. D.
【正确答案】D

【分析】根据合并同类项，同底幂乘法，同底幂除法，单项式乘单项式运算法则逐一计算作出判断即可.
【详解】A．和没有是同类项，没有可合并，故本选项错误；
B．，故本选项错误；
C．，故本选项错误；
D．，故本选项正确．
故选D．
5. 若分式有意义,则a的取值范围是(     )
A. a≠2 B. a≠0 C. a≠2且a≠0 D. 一切实数
【正确答案】A

【详解】试题解析：根据题意得：a-2≠0，
解得：a≠2．
故选A．
6. 若,则A为(     )
A. 2ab B. -2ab C. 4ab D. -4ab
【正确答案】C

【详解】试题解析：∵（a+b）2=a2+2ab+b2，（a-b）2=a2-2ab+b2，
∴A=（a+b）2-（a-b）2=4ab．
故选C．
点睛：完全平方式：（a+b）2=a2+2ab+b2与（a-b）2=a2-2ab+b2两公式的联系，它们的差是两数乘积的四倍．
7. 下列各式能用平方差公式分解因式的有( )
①x2+y2；②x2﹣y2；③﹣x2﹣y2；④﹣x2+y2；⑤﹣x2+2xy﹣y2．
A. 4个 B. 3个 C. 2个 D. 1个
【正确答案】C

【详解】能用平方差公式分解因式的有；②x2-y2；④-x2+y2；，共2个，
故选C．
8. 如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（ ）

A. 1个 B. 2个 C. 3个 D. 4个
【正确答案】C

【详解】要使△ABP与△ABC全等，
必须使点P到AB的距离等于点C到AB的距离，
即3个单位长度，
所以点P的位置可以是P1，P2，P4三个，
故选C.．

9. 化简的结果是【 】
A. B. C. （x+1）2 D. （x﹣1）2
【正确答案】D

【详解】将原式括号中的两项通分并利用同分母分式的减法法则计算，分子合并，同时将除式的分母利用平方差公式分解因式，然后利用除以一个数等于乘以这个数的倒数将除法运算化为乘法运算，约分后即可得到最简结果：
．故选D
10. 某厂接到加工720件衣服的订单，预计每天做48件，正好按时完成，后因客户要求提前5天交货，设每天应多做x件，则x应满足的方程为（ ）
A. B.
C. D.
【正确答案】D

【分析】本题的关键是要弄清因客户要求工作量提速后的工作效率和工作时间，然后根据题目给出的关键语“提前5天”找到等量关系，然后列出方程．
【详解】因客户的要求每天的工作效率应该为：（48+x）件，所用的时间为：，根据“因客户要求提前5天交货”，用原有完成时间，减去提前完成时间，可以列出方程：
故选：D．
此题考查了分式方程的应用，这道题的等量关系比较明确，直接分析题目中的语句即可得知，再利用等量关系列出方程．
11. 已知关于x的分式方程+=1的解是非负数，则m的取值范围是（　　）
A. m＞2 B. m≥2 C. m≥2且m≠3 D. m＞2且m≠3
【正确答案】C

【详解】分式方程去分母得：m-3=x-1，
解得：x=m-2，
由方程的解为非负数，得到m-2≥0，且m-2≠1，
解得：m≥2且m≠3．
故选C.

12. 如图，已知△ABE≌△ACD，下列选项中没有能被证明的等式是( )

A. AD＝AE B. DB＝AE C. DF＝EF D. DB＝EC
【正确答案】B

【详解】试题解析：∵△ABE≌△ACD，
∴AB=AC，AD=AE，∠B=∠C，故A正确；
∴AB-AD=AC-AE，即BD=EC，故D正确；
在△BDF和△CEF中

∴△BDF≌△CEF（ASA），
∴DF=EF，故C正确；
故选B．
二、填 空 题（每小题4分，共24分）
13. 若一个多边形外角和与内角和相等，则这个多边形是_____．
【正确答案】四边形．

【分析】根据多边形的内角和公式与多边形的外角和定理列出方程，然后解方程即可求出多边形的边数：
【详解】解：设这个多边形的边数是n，则
（n﹣2）•180°=360°，
解得n=4．
∴这个多边形是四边形．
本题考查了多边形内角和公式的应用，解题的关键是要能列出一元方程．
14. 分解因式：x2y﹣4xy+4y＝_____．
【正确答案】y(x-2)2

【分析】先提取公因式y，再根据完全平方公式分解即可得.
【详解】原式==，
故答案为．
15. 如图，△ABC≌△A′B′C′，其中∠A=36°，∠C′=24°，则∠B=______度．

【正确答案】120

【分析】根基三角形全等的性质得到∠C=∠C′=24°，再根据三角形的内角和定理求出答案.
【详解】∵，
∴∠C=∠C′=24°，
∵∠A+∠B+∠C=180°，∠A=36°，
∴∠B=120°，
故120.
此题考查三角形全等的性质定理：全等三角形的对应角相等，三角形的内角和定理.
16. 已知4y2+my+1是完全平方式，则常数m的值是______．
【正确答案】4或-4

【详解】解：∵4y2-my+1是完全平方式，
∴-m=±4，即m=±4．
故答案为4或-4.
17. 如图，点P是∠AOB内部一点，∠AOB=30°，OP=8cm，M，N是OA，OB上的两个动点，则△MPN周长的最小值_____cm．

【正确答案】8

【分析】设点P关于OA的对称点为C，关于OB的对称点为D，当点M、N在CD上时，△PMN的周长最小．
【详解】分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M、N，连接OP、OC、OD、PM、PN．
∵点P关于OA的对称点为C，关于OB的对称点为D，
∴PM=CM，OP=OC，∠COA=∠POA；

∵点P关于OB的对称点为D，
∴PN=DN，OP=OD，∠DOB=∠POB，
∴OC=OD=OP=8cm，∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°，
∴△COD是等边三角形，
∴CD=OC=OD=8cm．
∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DN=CD=8cm．
故答案为8．
此题考查轴对称--最短路线问题，熟知两点之间线段最短是解题的关键．
18. 若分式方程无解,则k=__________
【正确答案】3和1

【详解】试题解析：方程去分母得：3（x-3）+2-kx=-1，
整理得（3-k）x=6，
当整式方程无解时，3-k=0即k=3，
当分式方程无解时，x=3，此时3-k=2，k=1，
所以k=3或1时，原方程无解．
故答案为3或1．
三、解 答 题：（简答题要写出必要的解题步骤和证明过程，共78分）
19. （1）分解因式：① ， ②；
（2）已知a+b=2,求值.
【正确答案】(1)①-y（3x-y）2; ②(4x2+1)(2x+1)(2x-1) (2) ，.

【分析】（1）①先提取公因式-y，再对余下的多项式利用完全平方公式继续分解．
②两次运用平方差公式进行分解即可；
（2）先化简题目中的式子，然后将a+b的值代入化简后的式子即可解答本题．
【详解】（1）①6xy2-9x2y-y3
=-y（y2-6xy+9x2）
=-y（y-3x）2．
②16x4-1
=（4x2+1）（4x2-1）
=（4x2+1）（2x+1）（2x-1）．
（2）
=
=
=，
当a+b=2时，原式=．
20. 已知，如图 ，在△ABC中，∠C=∠ABC=2∠A，BD是AC边上的高，求∠DBC的度数

【正确答案】18°

【分析】先设∠A＝x°，则∠C＝∠ABC＝2x°，根据三角形内角和定理列出方程求得x的值，再根据直角三角形性质求解即可．
【详解】解：△ABC中，∠C=∠ABC=2∠A，
设∠A=x°，
则∠C=∠ABC=2x°，
∴x+2x+2x=180，
解得：x=36，
∴∠C=2x°=72°，
在△BDC中， BD是AC边上的高，
∴∠BDC=90°，
∴∠DBC=180°－90°－72°=18°．
本题主要考查了三角形内角和定理与直角三角形性质的运用，根据三角形内角和建构方程，熟练掌握相关概念是解题关键．

21. 如图,点A、D、E在直线l上,∠BAC=90°,AB=AC,BD⊥l于D,CE⊥l于E,求证:DE=BD+CE.

【正确答案】证明见解析.

【分析】根据已知条件及互余关系可证△ABD≌△CAE，则BD=AE，AD=CE，由DE=AD+AE，得出线段DE=BD+CE．
【详解】∵∠BAC=90°，BD⊥DE，CE⊥DE，
∴∠DAB+∠DBA=∠DAB+∠EAC，
∴∠DBA=∠EAC；
在△ABD与△CAE中，
，
∴△ABD≌△CAE（AAS），
∴BD=AE，AD=CE，
∴DE=BD+CE．
22. 如图，已知Rt△ABC中,∠ACB=90°,CD⊥AB于D,∠BAC的平分线分别交BC、CD于E、F.试说明△CEF是等腰三角形.

【正确答案】说明见解析.

【详解】试题分析：要证明△CEF是等腰三角形，需证明有两角相等即可．利用角平分线、直角三角形及三角形外角的性质，进行等量代换，可求证．
解：∵∠ACB＝90°，
∴∠B＋∠BAC＝90°.
∵CD⊥AB，
∴∠CAD＋∠ACD＝90°.∴∠ACD＝∠B.
∵AE是∠BAC的平分线，∴∠CAE＝∠EAB.
∵∠EAB＋∠B＝∠CEA，∠CAE＋∠ACD＝∠CFE，
∴∠CFE＝∠CEF.∴CF＝CE.
∴△CEF是等腰三角形．
23. 如图,在平面直角坐标系中,A(-1，5)，B（-1，0），C（-4，3）.

（1）在图中作出△ABC关于y轴的对称图形△A1B1C1；
（2）写出点A1、B1、C1的坐标；
（3）在y轴上画出点P，使PA+PC最小；  
（4）求六边形AA1C1B1BC的面积．.
【正确答案】（1）作图见解析；（2）A1（1，5）、B1（1，0）、C1（4，3）；（3）见解析；（4）25.

【详解】试题分析：（1）根据题意画出△A1B1C1即可；
（2）根据△A1B1C1在坐标系中的位置即可得出各点坐标；
（3）连接A1C与y轴交于点P，则P点即为所求；
（4）根据S六边形AA1C1B1BC=S△ABC+S△A1B1C1+S矩形AA1C1B1B即可得出结论．
试题解析：（1）如图所示；

（2）由图可知，A1（1，5）、B1（1，0）、C1（4，3）；
（3）连接A1C与y轴交于点P，则P点即为所求；
（4）S六边形AA1C1B1BC=S△ABC+S△A1B1C1+S矩形AA1C1B1B
=×5×3+×5×3+2×5
=15+10
=25．
24. 甲、乙、丙三个登山爱好者经常相约去登山，今年1月甲参加了两次登山．
（1）1月1日甲与乙同时开始攀登一座900米高的山，甲的平均攀登速度是乙的1.2倍，结果甲比乙早15分钟到达顶峰．求甲的平均攀登速度是每分钟多少米？
（2）1月6日甲与丙去攀登另一座h米高的山，甲保持第（1）问中的速度没有变，比丙晚出发0.5小时，结果两人同时到达顶峰，问甲的平均攀登速度是丙的多少倍？（用含h的代数式表示）
【正确答案】（1）甲的平均攀登速度是12米/分钟；（2）倍.

【分析】（1）根据题意可以列出相应的分式方程，从而可以求得甲的平均攀登速度；
（2）根据（1）中甲的速度可以表示出丙的速度，再用甲的速度比丙的平均攀登速度即可解答本题．
【详解】（1）设乙的速度为x米/分钟，
，
解得，x=10，
经检验，x=10是原分式方程的解，
∴1.2x=12，
即甲的平均攀登速度是12米/分钟；
（2）设丙的平均攀登速度是y米/分，
+0.5×60＝，
化简，得
y=，
∴甲的平均攀登速度是丙的：倍，
即甲的平均攀登速度是丙的倍．
25. 已知∠MAN=120°，点C是∠MAN的平分线AQ上的一个定点，点B，D分别在AN，AM上，连接BD．
【发现】
（1）如图1，若∠ABC=∠ADC=90°，则∠BCD=　 　°，△CBD是　 　三角形；
【探索】
（2）如图2，若∠ABC+∠ADC=180°，请判断△CBD的形状，并证明你的结论；
【应用】
（3）如图3，已知∠EOF=120°，OP平分∠EOF，且OP=1，若点G，H分别在射线OE，OF上，且△PGH为等边三角形，则满足上述条件的△PGH的个数一共有　 　．（只填序号）
①2个 ②3个 ③4个 ④4个以上

【正确答案】（1）60，等边；（2）等边三角形，证明见解析（3）④.

【分析】（1）利用四边形的内角和即可得出∠BCD的度数，再利用角平分线的性质定理即可得出CB，即可得出结论；
（2）先判断出∠CDE=∠ABC，进而得出△CDE≌△CFB（AAS），得出CD=CB，再利用四边形的内角和即可得出∠BCD=60°即可得出结论；
（3）先判断出∠POE=∠POF=60°，先构造出等边三角形，找出特点，即可得出结论．
【详解】（1）如图1，连接BD，

∵∠ABC=∠ADC=90°，∠MAN=120°，
根据四边形的内角和得，∠BCD=360°-（∠ABC+∠ADC+∠MAN）=60°，
∵AC是∠MAN的平分线，CD⊥AM．CB⊥AN，
∴CD=CB，（角平分线的性质定理），
∴△BCD是等边三角形；
故答案为60，等边；
（2）如图2，同（1）得出，∠BCD=60°（根据三角形的内角和定理），

过点C作CE⊥AM于E，CF⊥AN于F，
∵AC是∠MAN的平分线，
∴CE=CF，
∵∠ABC+∠ADC=180°，∠ADC+∠CDE=180°，
∴∠CDE=∠ABC，
△CDE和△CFB中，
，
∴△CDE≌△CFB（AAS），
∴CD=CB，
∵∠BCD=60°，
∴△CBD是等边三角形；
（3）如图3，

∵OP平分∠EOF，∠EOF=120°，
∴∠POE=∠POF=60°，在OE上截取OG'=OP=1，连接PG'，
∴△G'OP是等边三角形，此时点H'和点O重合，
同理：△OPH是等边三角形，此时点G和点O重合，
将等边△PHG绕点P逆时针旋转到等边△PG'H'，在旋转的过程中，
边PG，PH分别和OE，OF相交（如图中G''，H''）和点P围成的三角形全部是等边三角形，（旋转角的范围为（0°到60°包括0°和60°），
所以有无数个；
理由：同（2）的方法．
故答案为④．















2022-2023学年辽宁省鞍山市八年级上册数学期末专项提升模拟卷（B卷）
一、选一选：（本大题12个小题，每小题3分，共36分，在每小题给出的四个选项中只有一个是正确的，请把答题卡上对应题目所选的选项涂黑）
1. 下面有4个汽车标志图案，其中没有是轴对称图形是（ ）
A. B. C. D.
2. 下列实际情景运用了三角形稳定性的是（ ）
A. 人能直立在地面上 B. 校门口的自动伸缩栅栏门
C. 古建筑中三角形屋架 D. 三轮车能在地面上运动而没有会倒
3. 下列计算正确的是（ ）
A. a3·a4＝a12 B. (a3)4＝a7
C. (a2b)3＝a6b3 D. a3÷a4＝a(a≠0)
4. 没有能用尺规作图作出三角形的是（　 　）
A. 已知两角和夹边 B. 已知两边和夹角
C. 已知两角和其中一角的对边 D. 已知两边和其中一边的对角
5. 下列从左边到右边的变形，是因式分解的是（ 　）
A. （3-x）（3+x）=9-x2 B. x2+2x+1＝x(x+1)+1
C. a2b+ab2=ab（a+b） D. (a-b)(n-m)=(b-a)(n-m)
6. 根据分式的基本性质可知，＝ ( )
A. a2 B. b2 C. ab D. ab2
7. 如图，已知E，B，F，C四点在一条直线上，，，添加以下条件之一，仍没有能证明≌的是　　

A. B. C. D.
8. 将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的度数为（ ）

A 75° B. 65° C. 60° D. 45°

9. 如图，若OP平分，，，垂足分别是C、D，则下列结论中错误的是　　

A. B.
C. D.

10. 在平面镜里看到背后墙上的电子钟示数如图所示，这时的实际时间应是（ ）

A. 21:02 B. 21:05 C. 20:15 D. 20:05
11. 若关于x的方程有增根，则k的值为( )．
A. 3 B. 1 C. 0 D. －1
12. 已知：2+=22×；3+=32×；4+=42×；5+=52×…，若10+=102×符合前面式子的规律，则a+b=（ ）
A. 99 B. 109 C. 100 D. 120
二、填 空 题（本大题共有6小题，每小题4分，共24分）
13. 请写出一个多项式（至多三项），使它能先“提公因式”，再“运用公式”来分解因式.
你编写的多项式是：_______________，分解因式的结果是________________.
14. 由于自然环境的日益恶化，我们赖以生存的空气质量正在悄悄地变化．净化的空气的单位体积质量为0.00124g/cm3，将它用科学记数表示为____________g/cm3．
15. 已知m2－2m－1=0，则代数式2m2－4m+2017的值为_______________.
16. 当三角形中一个内角α是另一个内角β一半时，我们称此三角形为“半角三角形”，其中α称为“半角”．如果一个“半角三角形”的“半角”为20°，那么这个“半角三角形”的内角的度数为__________．
17. 如图是小李绘制的某大桥断裂的现场草图，若∠1＝38°，∠2＝23°，则桥面断裂处夹角∠BCD＝__________.

18. 如图，小新从A点出发，沿直线前进50米后向左转30°，再沿直线前进50米，又向左转30°，…照这样下去，小新次回到出发地A点时，一共走了__米．

三、解 答 题（本大题共8小题，满分90分.解答需写出文字说明、证明过程和演算步骤）
19. 先化简再求值：，其中a=2
20. 解分式方程：=
21. 计算：
（1）+|﹣|+（）0
（2）已知：a﹢b＝4，ab ＝ 3，求：a2﹢b2的值．
22. 如图所示，在直角坐标系xOy中，△ABC三点的坐标分别A(－l，0)，B(－4，4)，C(0，3)．
（1）在图中画出△ABC关于y轴对称的图形△A1B1C1；写出B1的坐标为___________.
（2）填空：在图中，若B2(－4，－4)与点B关于一条直线成轴对称，则这条对称轴是________，此时点C关于这条直线的对称点C2的坐标为_____________；
（3）在y轴上确定一点P，使△APB的周长最小.(注：简要说明作法，保留作图痕迹，没有求坐标)

23. 某人驾车从A地到B地，出发2小时后车子出了点毛病，耽搁了半小时修车，为了弥补耽搁的时间他将车速增加到原来的1.6倍，结果按时到达，已知A、B两地相距100千米，求某人原来驾车的速度.
24. 探究归纳题：

(1)试验分析：
如图1，A点可以做__________条对角线；同样，B点可以做__________条；C点可以做__________条；D点可以做__________条对角线.
通过以上分析和总结，图1共有___________条对角线.
（2）拓展延伸：
运用（1）分析方法，可得：
图2共有_____________条对角线；
图3共有_____________条对角线；
(3)探索归纳：
对于n边形(n>3)，共有_____________条对角线．(用含n的式子表示)
(4)特例验证：
十边形有__________________对角线.
25. 自学下面材料后，解答问题．
分母中含有未知数的没有等式叫做分式没有等式．如：＞0；＜0等．那么如何求出它们的解集呢？
根据我们学过的有理数除法法则可知：两数相除，同号得正，异号得负．其字母表达式为：
(1)若a＞0，b＞0，则＞0；若a＜0，b＜0，则＞0；
(2)若a＞0，b＜0，则＜0；若a＜0，b＞0，则＜0.
反之：①若＞0，则 或，
②若＜0，则 或．
根据上述规律，①求没有等式< 0的解集．
②直接写出没有等式解集为x>3或x3)，共有_____________条对角线．(用含n的式子表示)
(4)特例验证：
十边形有__________________对角线.
【正确答案】 ①. 1 ②. 1 ③. 1 ④. 1 ⑤. 2 ⑥. 5 ⑦. 9 ⑧. ⑨. 35

【分析】(1)根据对角线的定义,四边形任意一点可以做1条对角线,其中会出现重复,因此四边形共有2条对角线,
(2)五边形任意一点可以做2条对角线,其中会出现重复,因此四边形共有5条对角线, 六边形任意一点可以做3条对角线,其中会出现重复,因此四边形共有9条对角线,
(3) n边形任意一点可以做(n－3)条对角线,其中会出现重复,因此四边形共有条对角线,
(4) 十边形任意一点可以做7条对角线,其中会出现重复,因此四边形共有35条对角线.
【详解】(1) 四边形任意一点可以做1条对角线,其中会出现重复,因此四边形共有2条对角线,
(2)五边形任意一点可以做2条对角线,其中会出现重复,因此四边形共有5条对角线, 六边形任意一点可以做3条对角线,其中会出现重复,因此四边形共有9条对角线,
(3) n边形任意一点可以做(n－3)条对角线,其中会出现重复,因此四边形共有条对角线,
(4) 十边形任意一点可以做7条对角线,其中会出现重复,因此四边形共有35条对角线.
25. 自学下面材料后，解答问题．
分母中含有未知数的没有等式叫做分式没有等式．如：＞0；＜0等．那么如何求出它们的解集呢？
根据我们学过的有理数除法法则可知：两数相除，同号得正，异号得负．其字母表达式为：
(1)若a＞0，b＞0，则＞0；若a＜0，b＜0，则＞0；
(2)若a＞0，b＜0，则＜0；若a＜0，b＞0，则＜0.
反之：①若＞0，则 或，
②若＜0，则 或．
根据上述规律，①求没有等式< 0的解集．
②直接写出没有等式解集为x>3或x3或x