扬州市江都区实验初级中学2021-2022学年七年级3月月考数学试题（含解析）

这是一份扬州市江都区实验初级中学2021-2022学年七年级3月月考数学试题（含解析），共23页。试卷主要包含了 下列现象， 下列运算正确的是， xm＝2，xn＝4，则的值为等内容，欢迎下载使用。
扬州市江都区实验初级中学2021-2022学年七年级3月月考数学试题
一．选择题：（本大题共8小题，每小题3分，共24分）
1. 下列现象：①荡秋千小朋友；②打气筒打气时，活塞的运动；③钟摆的摆动；④传送带上瓶装饮料的移动．其中属于平移的是（ ）
A. ①② B. ①③ C. ②③ D. ②④
2. 下列运算正确的是（ ）
A. B. C. D.
3. 下面四个图形中，线段是的高的是（ ）
A. B.
C. D.
4. xm＝2，xn＝4，则的值为（ ）
A. 16 B. 48 C. 256 D. 128
5. 下列每组数表示3根小木棒的长度(单位：cm)，其中能用3根小木棒搭成一个三角形的是（ ）
A. 3，4，7 B. 3，4，6 C. 5，7，12 D. 2，3，6
6. 具备下列条件△ABC中，不是直角三角形的是（　　）
A. ∠A+∠B=∠C
B. ∠A=∠B=∠C
C. ∠A：∠B：∠C=1：2：3
D. ∠A=2∠B=3∠C
7. 如图，在△ABC中，∠A＝48°，∠ABC与∠ACD的平分线交于点A1，得∠A1；∠A1BC与∠A1CD的平分线相交于点A2，得∠A2；……；∠An－1BC与∠An－1CD的平分线交于点An，要使∠An的度数为整数，则n的最大值为(　　)

A. 2 B. 3 C. 4 D. 5
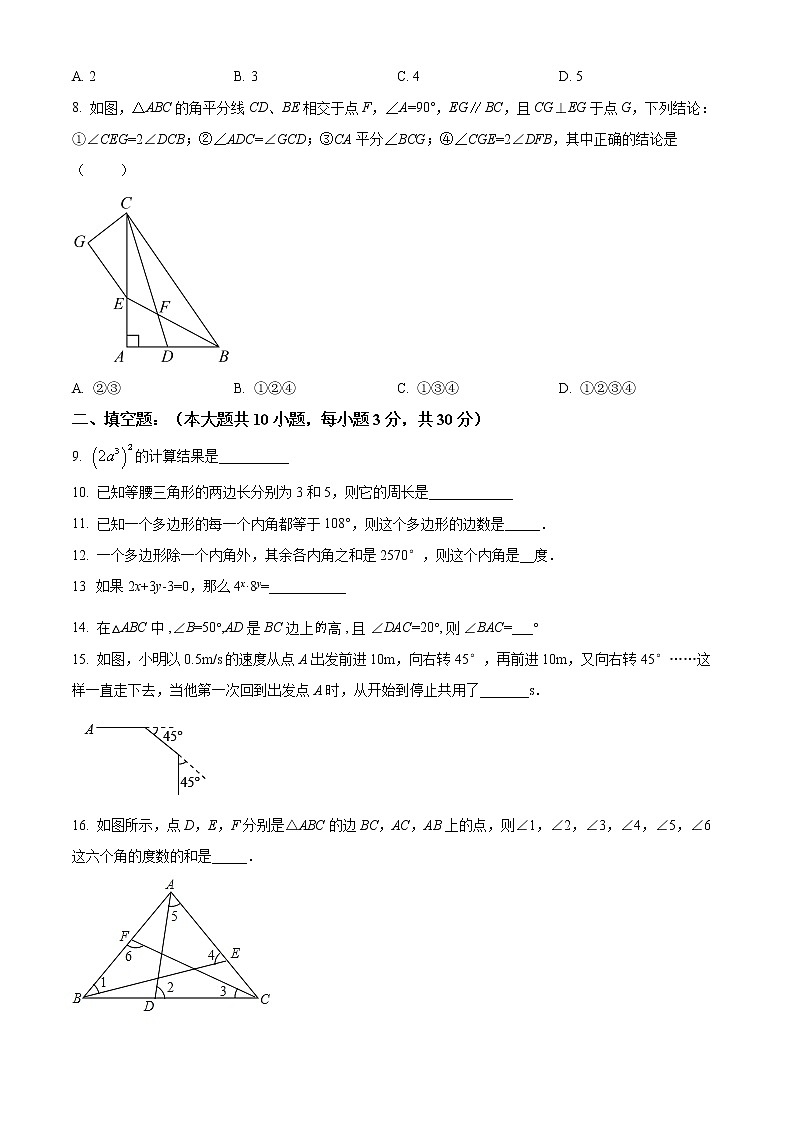
8. 如图，△ABC的角平分线CD、BE相交于点F，∠A=90°，EGBC，且CG⊥EG于点G，下列结论：①∠CEG=2∠DCB；②∠ADC=∠GCD；③CA平分∠BCG；④∠CGE=2∠DFB，其中正确的结论是（ ）

A. ②③ B. ①②④ C. ①③④ D. ①②③④
二、填空题：（本大题共10小题，每小题3分，共30分）
9. 的计算结果是__________
10. 已知等腰三角形的两边长分别为3和5，则它的周长是____________
11. 已知一个多边形的每一个内角都等于108°，则这个多边形的边数是_____．
12. 一个多边形除一个内角外，其余各内角之和是2570°，则这个内角是__度．
13 如果2x+3y-3=0，那么4x·8y=___________
14. 在△ABC 中 ,∠B=50°,AD是BC 边上高 , 且 ∠DAC=20°, 则 ∠BAC=___°
15. 如图，小明以0.5m/s的速度从点A出发前进10m，向右转45°，再前进10m，又向右转45°……这样一直走下去，当他第一次回到出发点A时，从开始到停止共用了_______s．

16. 如图所示，点D，E，F分别是△ABC的边BC，AC，AB上的点，则∠1，∠2，∠3，∠4，∠5，∠6这六个角的度数的和是_____．

17. 如图，四边形ABCD中，点M，N分别在AB，BC上， 将沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B =___°．

18. 如图，△ABC中，D是AB的中点，且AE：CE=2：1，S△CEP=1，则△ABC=_____________

三．解答题：（本大题共10小题，共96分）
19. 计算
（1）9×27-3×
（2）
20. 先化简，再求值：，其中x=0.5，y=2
21. 如图，每个小正方形的边长为1，△ABC经过平移得到△A′B′C′，根据下列条件，利用网格点和直尺画图：

（1）补全△A′B′C′；
（2）作出中线CD；
（3）画出BC边上的高线AE；
（4）△ABC面积为____．
22. 如图，∠A=65°，∠ABD=30°，∠ACB=72°，且CE平分∠ACB，求∠BEC的度数．

23. （1）已知，求n的值．
（2）已知，其中a、b、c为正整数，求的值．
24. 如图，在△ABC中，AD是高，AE是∠BAC的平分线，若∠ABC=40°，∠ACB=70°，求∠EAD的度数．

25. 如图，已知：CF⊥AB于F，ED⊥AB于D，∠1＝∠2，求证：FG∥BC．

26. 如图，在四边形ABCD中，∠A=∠C=90°，点E、F分别在DC、AB上，且BE、DF分别在DC、AB上，且BE、DF分别平分∠ABC、∠ADC．判断BE、DF是否平行，并说明理由．

27. 如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F
（1）当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为______；
（2）当△PMN所放位置如图②所示时，求证：∠PFD−∠AEM＝90°；
（3）在（2）的条件下，若MN与CD交于点O，且∠DON＝30°，∠PEB＝15°，求∠N的度数．

28. 在中，三个内角的平分线交于点O，过点O作，交边BC于点D．

（1）如图1，求的度数；
（2）如图2，作外角的平分线交CO的延长线于点F．
①对进行说理；
②若，求的度数．
答案与解析
一．选择题：（本大题共8小题，每小题3分，共24分）
1. 下列现象：①荡秋千的小朋友；②打气筒打气时，活塞的运动；③钟摆的摆动；④传送带上瓶装饮料的移动．其中属于平移的是（ ）
A. ①② B. ①③ C. ②③ D. ②④
【答案】D
【解析】
【分析】根据平移的性质可知．
【详解】解：①荡秋千的小朋友是旋转，不属于平移，不符合题意；
②打气筒打气时，活塞的运动属于平移，符合题意；
③钟摆的摆动是旋转，不属于平移，不符合题意；
④传送带上瓶装饮料的移动符合平移的性质，属于平移，符合题意．
故选D．
【点睛】本题考查图形的平移变换．图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转，以致选错．
2. 下列运算正确的是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】根据合并同类项，同底数幂乘法以及积的乘方公式进行计算即可．
详解】解：A．，不符合题意；
B．，不符合题意；
C．，不符合题意；
D．，符合题意．
故选：D．
【点睛】本题考查了合并同类项，同底数幂乘法以及积的乘方公式运算，正确地计算能力是解决问题的关键．
3. 下面四个图形中，线段是高的是（ ）
A. B.
C. D.
【答案】A
【解析】
【分析】根据三角形高的画法知，过点B作AC边上的垂线，垂足为D，其中线段BD是△ABC的高，再结合图形进行判断．
【详解】A选项中，BD与AC垂直,符合要求；
B选项中，BD与AC不垂直；
C选项中，BD与AC不垂直；
D选项中，BD与AC不垂直；
故选：A．
【点睛】本题主要考查了三角形的高，三角形的高是指从三角形的一个顶点向对边作垂线，连接顶点与垂足之间的线段．
4. xm＝2，xn＝4，则的值为（ ）
A. 16 B. 48 C. 256 D. 128
【答案】C
【解析】
【分析】根据同底数幂的乘法的逆用和幂的乘方的逆用计算即可．
【详解】，
将xm＝2，xn＝4代入，得：，
故选C．
【点睛】本题考查同底数幂的乘法的逆用和幂的乘方的逆用．掌握同底数幂的乘法的逆运算和幂的乘方的逆运算法则是解题关键．
5. 下列每组数表示3根小木棒的长度(单位：cm)，其中能用3根小木棒搭成一个三角形的是（ ）
A. 3，4，7 B. 3，4，6 C. 5，7，12 D. 2，3，6
【答案】B
【解析】
【详解】A.，不能构成三角形，故本选项不符合题意；
B.，能构成三角形，故本选项符合题意；
C.，不能构成三角形，故本选项不符合题意；
D.，不能构成三角形，故本选项不符合题意．
故选：B．
【点睛】本题考查三角形的三边关系：三角形任意两边之和大于第三边．
6. 具备下列条件的△ABC中，不是直角三角形的是（　　）
A. ∠A+∠B=∠C
B. ∠A=∠B=∠C
C. ∠A：∠B：∠C=1：2：3
D. ∠A=2∠B=3∠C
【答案】D
【解析】
【分析】根据三角形内角和180°，直接进行解答．
【详解】解：A中∠A+∠B=∠C，即2∠C=180°，∠C=90°，为直角三角形，同理，B，C均为直角三角形， D选项中∠A=2∠B=3∠C，即3∠C +∠C +∠C =180°，∠C =，三个角没有90°角，故不是直角三角形．
“点睛”本题考查三角形内角和定理以及直角的判定条件，熟知三角形内角和是180°是解答此题的关键．

7. 如图，在△ABC中，∠A＝48°，∠ABC与∠ACD的平分线交于点A1，得∠A1；∠A1BC与∠A1CD的平分线相交于点A2，得∠A2；……；∠An－1BC与∠An－1CD的平分线交于点An，要使∠An的度数为整数，则n的最大值为(　　)

A. 2 B. 3 C. 4 D. 5
【答案】C
【解析】
【分析】由三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD＝∠ABC＋∠A，∠A1CD＝∠A1BC＋∠A1，根据角平分线的定义可得∠A1BC＝∠ABC，∠A1CD＝∠ACD，然后整理得到∠A1＝∠A，根据A1B、A1C分别平分∠ABC、∠ACD可得：∠ABC＝2∠A1BC，∠ACD＝2∠A1CD，而∠ACD＝∠A＋∠ABC ，∠A1CD＝∠A1＋∠A1BC，于是有∠A＝2∠A1，同理可得∠A1＝2∠A2，继而∠A2＝∠A，因此发现规律，将∠A代入即可求出使∠An的度数为整数，则n的最大值．
【详解】由三角形的外角性质可得：∠ACD＝∠ABC＋∠A，∠A1CD＝∠A1BC＋∠A1，
∵∠ABC与∠ACD的平分线交于点A1，
∴∠A1BC＝∠ABC，∠A1CD＝∠ACD，
∴∠A1＋∠A1BC＝∠A1CD ＝（∠ABC＋∠A）＝∠A＋∠A1BC，
∴∠A1＝∠A＝×48°＝24°，
∵A1B、A1C分别平分∠ABC、∠ACD，
∴∠ABC＝2∠A1BC，∠ACD＝2∠A1CD，
而∠ACD＝∠A＋∠ABC ，∠A1CD＝∠A1＋∠A1BC，
∴∠A＝2∠A1，
∴∠A1＝∠A,
同理可得：∠A1＝2∠A2，
∴∠A2＝∠A，
∴∠A＝2n∠An，
∴∠An＝∠A
∵∠A＝48°
∴当n＝4时，∠A4＝×48°＝3°，此时n的值最大，
故选：C
【点睛】本题考查了三角形外角性质、角平分线的性质、熟练掌握这两个性质并准确识图找出规律是解题的关键．
8. 如图，△ABC的角平分线CD、BE相交于点F，∠A=90°，EGBC，且CG⊥EG于点G，下列结论：①∠CEG=2∠DCB；②∠ADC=∠GCD；③CA平分∠BCG；④∠CGE=2∠DFB，其中正确的结论是（ ）

A. ②③ B. ①②④ C. ①③④ D. ①②③④
【答案】B
【解析】
【分析】根据平行线的性质、角平分线的定义、垂直的性质及三角形内角和定理依次判断即可得出答案．
【详解】解：①∵EGBC，
∴∠CEG=∠ACB，
又∵CD是△ABC的角平分线，
∴∠CEG=∠ACB=2∠DCB，故正确；
②∵∠A=90°，
∴∠ADC+∠ACD=90°，
∵CD平分∠ACB，
∴∠ACD=∠BCD，
∴∠ADC+∠BCD=90°．
∵EGBC，且CG⊥EG，
∴∠GCB=90°，即∠GCD+∠BCD=90°，
∴∠ADC=∠GCD，故正确；
③条件不足，无法证明CA平分∠BCG，故错误；
④∵CG⊥EG，
∴∠CGE=90°，
∵∠EBC+∠ACB=∠AEB，∠DCB+∠ABC=∠ADC，
∴∠AEB+∠ADC=90°+（∠ABC+∠ACB）=135°，
∴∠DFE=360°-135°-90°=135°，
∴∠DFB=45°
∴∠CGE=2∠DFB，故正确．
故选B．
【点睛】本题主要考查了角平分线的定义，平行线的性质，三角形内角和定理及多边形内角和，三角形外角的性质，熟知直角三角形的两锐角互余是解答此题的关键．
二、填空题：（本大题共10小题，每小题3分，共30分）
9. 的计算结果是__________
【答案】

【解析】
【分析】直接利用积的乘方的运算求解即可．
【详解】解：，
故答案为：．
【点睛】题目主要考查积的乘方的运算，熟练掌握运算法则是解题关键．
10. 已知等腰三角形的两边长分别为3和5，则它的周长是____________
【答案】11或13
【解析】
【分析】题目给出等腰三角形有两条边长为3和5，而没有明确腰、底分别是多少，所以要进行讨论，还要应用三角形三边关系验证能否组成三角形．
【详解】解：有两种情况：①腰长为3，底边长为5，三边为：3，3，5可构成三角形，周长=3+3+5=11；
②腰长为5，底边长为3，三边为：5，5，3可构成三角形，周长=5+5+3=13．
故答案为11或13．
【点睛】本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．
11. 已知一个多边形的每一个内角都等于108°，则这个多边形的边数是_____．
【答案】5
【解析】
【详解】解：∵多边形的每一个内角都等于108°
∴每一个外角为72°
∵多边形的外角和为360°
∴这个多边形的边数是：360÷72=5
故答案为：5
12. 一个多边形除一个内角外，其余各内角之和是2570°，则这个内角是__度．
【答案】130
【解析】
【分析】设出相应的边数和未知的那个内角度数，利用内角和公式列出相应等式，根据边数为整数求解即可．
【详解】解：设这个内角度数为x°，边数为n，
则（n﹣2）×180﹣x＝2570，
180•n＝2930+x，
∴n＝，
∵n为正整数，0°＜x＜180°，
∴n＝17，
∴这个内角度数为180°×（17﹣2）﹣2570°＝130°．
故答案为：130．
【点睛】本题主要考查多边形内角和公式的灵活运用，解题的关键是找到相应度数的等量关系．注意多边形的一个内角一定大于0°，并且小于180°．
13. 如果2x+3y-3=0，那么4x·8y=___________
【答案】8
【解析】
【分析】根据题意得出2x+3y=3，然后利用同底数幂的乘法及幂的乘方的逆运算进行计算即可．
【详解】解：∵2x+3y-3=0，
∴2x+3y=3，
∴，
故答案为：8．
【点睛】题目主要考查求代数式的值及同底数幂的乘法及幂的乘方的逆运算，熟练掌握运算法则是解题关键．
14. 在△ABC 中 ,∠B=50°,AD是BC 边上的高 , 且 ∠DAC=20°, 则 ∠BAC=___°
【答案】60°.
【解析】
【分析】根据直角三角形两锐角互余求出∠BAD，问题得解.
【详解】解：∵∠B=50°，AD是BC 边上的高，
∴∠BAD=90°-50°=40°，
∴∠BAC=∠BAD+∠DAC=40°+20°=60°，
故答案为60°.

【点睛】本题考查直角三角形的性质，熟练掌握三角形内角和定理及直角三角形两锐角互余是解题关键.
15. 如图，小明以0.5m/s的速度从点A出发前进10m，向右转45°，再前进10m，又向右转45°……这样一直走下去，当他第一次回到出发点A时，从开始到停止共用了_______s．

【答案】160
【解析】
【分析】根据题意，按照这个走法一直走下去，最终回到出发点时，走过的路程构成一个正多边形，这个正多边形的每个外角是45°，利用多边形外角和定理求解．
【详解】解：360°÷45°=8，
这是一个正八边形，
一共走了8×10=80米，
80÷0.5=160s．
故答案为：160．
【点睛】本题考查多边形的外角和定理，解题的关键是能够分析出走过的路程是一个正多边形．
16. 如图所示，点D，E，F分别是△ABC的边BC，AC，AB上的点，则∠1，∠2，∠3，∠4，∠5，∠6这六个角的度数的和是_____．

【答案】360°．
【解析】
【分析】利用三角形的外角的性质把这六个角转化到一个四边形中，即可求得结果．
【详解】解：不妨设AD和CF交于点M，BE和CF交于点N，
则∠AMC＝∠2+∠3，∠ENF＝∠1+∠6，
而∠AMC+∠ENF+∠4+∠5＝360°，
∴∠1+∠2+∠3+∠4+∠5+∠6＝360°．
故答案为：360°．

【点睛】本题主要考查三角形的外角的性质，解题的关键是把六个角转化到一个四边形中．
17. 如图，四边形ABCD中，点M，N分别在AB，BC上， 将沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B =___°．

【答案】95
【解析】
【详解】∵MF//AD，FN//DC，
∴∠BMF=∠A=100°，∠BNF=∠C=70°.
∵△BMN沿MN翻折得△FMN，
∴∠BMN=∠BMF=×100°=50°，∠BNM=∠BNF=×70°=35°.
在△BMN中，∠B=180°－（∠BMN＋∠BNM）=180°－（50°＋35°）=180°－85°=95°.
故答案为：95
18. 如图，△ABC中，D是AB的中点，且AE：CE=2：1，S△CEP=1，则△ABC=_____________

【答案】12
【解析】
【分析】连接AP，根据三角形中线的性质可得，，从而证出，然后求出，即可求出，结合图形即可求出结论．
【详解】解：连接AP,

∵D是AB的中点，
∴，，
∴，
∴，
∵AE：CE=2：1，，
∴
∴
∴，
∴，
∵AE：CE=2：1，
∴，
∴，
故答案为：12．
【点睛】此题考查的是三角形中线性质的应用，掌握三角形中线的性质是解题关键．
三．解答题：（本大题共10小题，共96分）
19. 计算
（1）9×27-3×
（2）
【答案】（1）0 （2）-
【解析】
【分析】（1）先计算乘方，再计算乘法，最后计算加减即可；
（2）先根据积的乘方与幂的乘方法则计算，再根据同底数幂相乘运算法则计算即可．
【小问1详解】
解：原式=9×27-3×81
=243-243
=0；
【小问2详解】
解：原式=
=-.
【点睛】本题考查有理数的混合运算，幂的运算，熟练掌握有理数混合运算法则与顺序、积的乘方与幂的乘方法则、同底数幂乘法法则是解题的关键．
20. 先化简，再求值：，其中x=0.5，y=2
【答案】，16
【解析】
【分析】先去括号，再合并同类项，然后把x，y的值代入化简后的式子进行计算即可解答．
【详解】解：


当x=0.5，y=2时，原式=
=2××64
=16．
【点睛】本题考查了整式的混合运算-化简求值，准确熟练地进行计算是解题的关键．
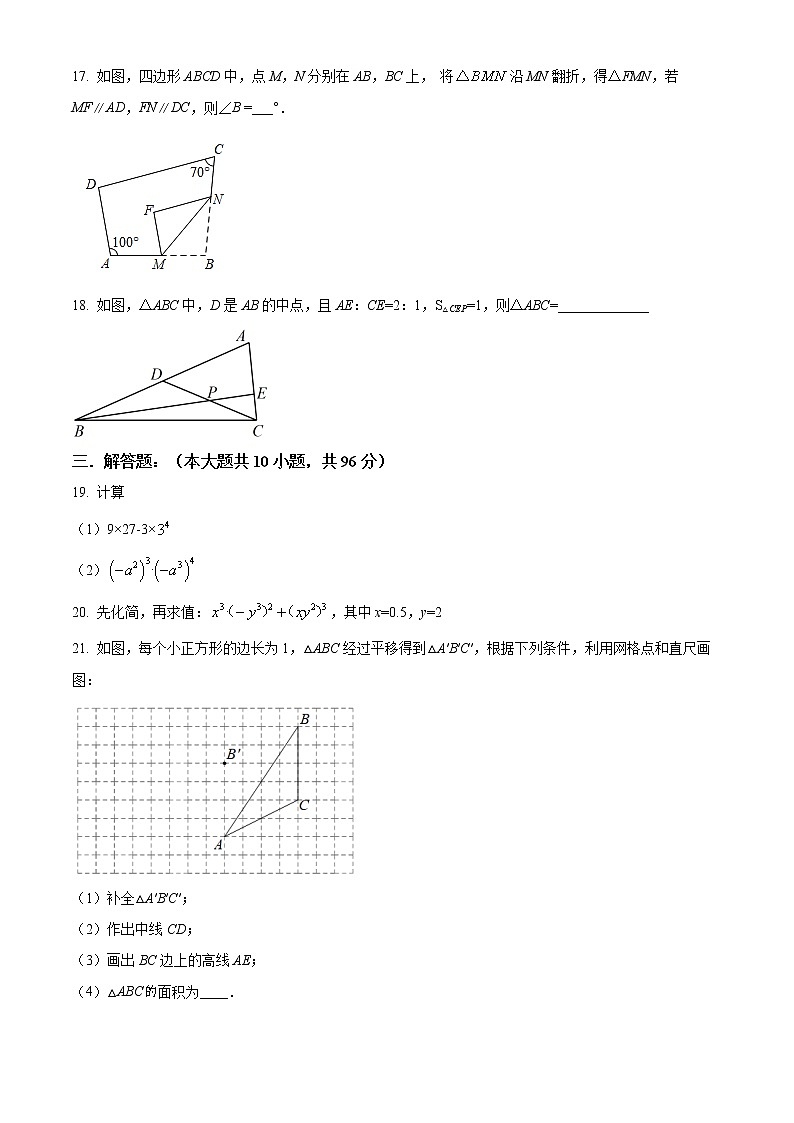
21. 如图，每个小正方形的边长为1，△ABC经过平移得到△A′B′C′，根据下列条件，利用网格点和直尺画图：

（1）补全△A′B′C′；
（2）作出中线CD；
（3）画出BC边上的高线AE；
（4）△ABC的面积为____．
【答案】（1）见解析 （2）见解析
（3）见解析 （4）8
【解析】
【分析】（1）分别作出A，B，C的对应点A′，B′，C′即可．
（2）根据中线的定义画出图形即可．
（3）根据高的定义画出图形即可．
（4）利用三角形面积公式求解即可．
【小问1详解】
如图，△A′B′C′即为所求．
【小问2详解】
如图线段CD即为所求．
【小问3详解】
如图，线段AE即为所求．
【小问4详解】

故答案为：8
【点睛】本题考查作图-应用与设计，三角形的面积等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
22. 如图，∠A=65°，∠ABD=30°，∠ACB=72°，且CE平分∠ACB，求∠BEC的度数．

【答案】131°
【解析】
【分析】先根据∠A=65°，∠ACB=72°得出∠ABC的度数，再由∠ABD=30°得出∠CBD的度数，根据CE平分∠ACB得出∠BCE的度数，根据∠BEC=180°-∠BCE-∠CBD即可得出结论．
【详解】解：在△ABC中，
∵∠A=65°，∠ACB=72°
∴∠ABC=43°
∵∠ABD=30°
∴∠CBD=∠ABC﹣∠ABD=13°
∵CE平分∠ACB
∴∠BCE=∠ACB=36°
∴在△BCE中，∠BEC=180°﹣13°﹣36°=131°．
【点睛】本题考察了三角形内角和定理，在两个三角形中，三个角之间的关系是解决此题的关键．
23. （1）已知，求n的值．
（2）已知，其中a、b、c为正整数，求的值．
【答案】（1）1 （2）1024
【解析】
【分析】（1）将变形为，将分别变形为，然后可计算，即可确定n的值；
（2）将3996分解质因数，分别求出a、b、c的值，然后代入计算的值即可．
【详解】解：（1）∵，
∴，
∴
∴，
∴，
∴；
（2）∵，，
∴，，，
∴


．
【点睛】本题主要考查了幂的乘方的逆运算以及代数式代入求值的知识，熟练掌握幂的乘方的逆运算是解题的关键．
24. 如图，在△ABC中，AD是高，AE是∠BAC的平分线，若∠ABC=40°，∠ACB=70°，求∠EAD的度数．

【答案】15°
【解析】
【分析】利用三角形的高线、角平分线的计算及三角形内角和定理求解即可．
【详解】解：在△ABC中，∠ABC＝40°，∠ACB＝70°，
∴∠BAC＝180°－∠ABC－∠ACB＝70°，
∵AE是∠BAC的平分线，
∴∠BAE＝∠CAE=∠BAC＝35°，
在△ABD中，∠ABC＋∠BAD＋∠BDA＝180°，
∵AD是高，所以∠BDA＝90°，
∴∠BAD＝180°－∠ABC－∠BDA＝180°－40°－90°＝50°，
∴∠DAE＝∠BAD－∠BAE＝50°－35°＝15°．
【点睛】题目主要考查三角形角平分线的计算、三角形内角和定理，理解题意，找准各角之间的关系是解题关键．
25. 如图，已知：CF⊥AB于F，ED⊥AB于D，∠1＝∠2，求证：FG∥BC．

【答案】证明见解析．
【解析】
【分析】通过ED⊥AB，CF⊥AB，证得DE∥CF，再由平行线的性质得∠1=∠BCF，进一步证得∠2=∠BCF，从而得到FG//BC．
【详解】∵ED⊥AB，CF⊥AB，
∴∠BDE=∠BFC=90，
∴DE∥CF，
∴∠1=∠BCF，
∵∠1=∠2，
∴∠2=∠BCF，
∴FG//BC．
26. 如图，在四边形ABCD中，∠A=∠C=90°，点E、F分别在DC、AB上，且BE、DF分别在DC、AB上，且BE、DF分别平分∠ABC、∠ADC．判断BE、DF是否平行，并说明理由．

【答案】平行，理由见解析
【解析】
【分析】根据角平分线的计算得出∠ADF=∠FDC，∠ABE=∠CBE，再由等角的余角相等得出∠AFD=∠ABE，利用平行线的判定即可证明．
【详解】解：BEDF，理由为：
四边形ABCD中，∠A＝∠C＝90°，
∴∠ADC＋∠ABC=180°，∠ADF＋∠AFD=90°，
∵BE平分∠ABC，DF平分∠ADC，
∴∠ADF=∠FDC，∠ABE=∠CBE，
∴∠ABE＋∠ADF=90°，
∵∠AFD＋∠ADF=90°，
∴∠AFD=∠ABE，
∴BEDF．
【点睛】题目主要考查平行线的判定定理及角平分线的计算，理解题意，找准各角之间的关系是解题关键．
27. 如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F
（1）当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为______；
（2）当△PMN所放位置如图②所示时，求证：∠PFD−∠AEM＝90°；
（3）在（2）的条件下，若MN与CD交于点O，且∠DON＝30°，∠PEB＝15°，求∠N的度数．

【答案】（1）∠PFD＋∠AEM=90°；（2）见解析；（3）45°
【解析】
【分析】（1）过点P作PH∥AB，然后根据平行于同一条直线的两直线平行可得PH∥AB∥CD，根据平行线的性质可得∠AEM=∠MPH，∠PFD=∠NPH，然后根据∠MPH＋∠NPH=90°和等量代换即可得出结论；
（2）过点P作PG∥AB，然后根据平行于同一条直线的两直线平行可得PG∥AB∥CD，根据平行线的性质可得∠AEM=∠MPG，∠PFD=∠NPG，然后根据∠NPG－∠MPG=90°和等量代换即可证出结论；
（3）设AB与PN交于点H，根据三角形的内角和定理即可求出∠PHE，然后根据平行线的性质可得∠PFO=∠PHE，然后根据三角形外角的性质即可求出结论．
【详解】解：（1）过点P作PH∥AB

∵AB∥CD，
∴PH∥AB∥CD，
∴∠AEM=∠MPH，∠PFD=∠NPH
∵∠MPN=90°
∴∠MPH＋∠NPH=90°
∴∠PFD＋∠AEM=90°
故答案为：∠PFD＋∠AEM=90°；
（2）过点P作PG∥AB

∵AB∥CD，
∴PG∥AB∥CD，
∴∠AEM=∠MPG，∠PFD=∠NPG
∵∠MPN=90°
∴∠NPG－∠MPG=90°
∴∠PFD－∠AEM=90°；
（3）设AB与PN交于点H

∵∠P=90°，∠PEB＝15°
∴∠PHE=180°－∠P－∠PEB＝75°
∵AB∥CD，
∴∠PFO=∠PHE=75°
∴∠N=∠PFO－∠DON=45°．
【点睛】此题考查的是平行线的判定及性质、三角形内角和定理和三角形外角的性质，掌握作平行线的方法、平行线的判定及性质、三角形内角和定理和三角形外角的性质是解决此题的关键．
28. 在中，三个内角平分线交于点O，过点O作，交边BC于点D．

（1）如图1，求的度数；
（2）如图2，作外角的平分线交CO的延长线于点F．
①对进行说理；
②若，求的度数．
【答案】（1）见解析 （2）①见解析；②100°
【解析】
【分析】（1）根据角平分线的定义，，，结合三角形的内角和定理，即可求出的度数；
（2）①根据角平分线的性质可得：∠EBF=90°-∠DBO，根据三角形的内角和定理，可得：∠ODB=90°-∠OBD，即可证明；②根据角平分线的性质和三角形的外角定理即可求解．
【小问1详解】
三个内角的平分线交于点O，
，
，
，
，
；
【小问2详解】
①理由如下：
平分，
，
，
，
∴
②BF平分，
，
三个内角的平分线交于点O，
，
，
，

【点睛】本题主要考查了三角形的内角和定理，三角形的外角定理，角平分线的性质，平行线的判定，熟练地掌握相关内容是解题的关键．