

2022-2023学年天津市宁河县八年级上册数学期末专项提升模拟题(AB卷)含解析
展开2022-2023学年天津市宁河县八年级上册数学期末专项提升模拟题(A卷)
一、选一选:本大题有 10 个小题,每小题 3 分,共 30 分.在每小题给出的四个选项中,只 有一项题目要求.
1. 已知 a=3cm,b=6cm,则下列长度的线段中,能与 a,b 组成三角形的是 ( )
A. 2cm B. 6cm C. 9cm D. 11cm
2. 在平面直角坐标系中,点 M(a2+1,-3)所在的象限是( )
A. 象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 正比例函数中,y随x的增大而减小,则k的取值范围是
A B. C. D.
4. 没有等式 1-x>0 的解在数轴上表示正确的是( )
A. B.
C. D.
5. 下列判断正确是( )
A. 两边和一角对应相等的两个三角形全等 B. 一边及一锐角相等的两个直角三角形全等
C. 顶角和底边分别相等的两个等腰三角形全等 D. 三个内角对应相等的两个三角形全等
6. 已知 a>b,则下列四个没有等式中,没有正确的是( )
A a -3> b -3 B. - a +2>- b +2 C. a>b D. 1+4a>1+4b
7. 已知(-1,y1),(1.8,y2),(-, y3 ) 是直线 y = -3x + m (m 为常数)上的三个点,则 y1,y2,y3的大小关系是( )
A. y3>y1>y2 B. y1>y3>y2 C. y1>y2>y3 D. y3>y2>y1
8. 如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )
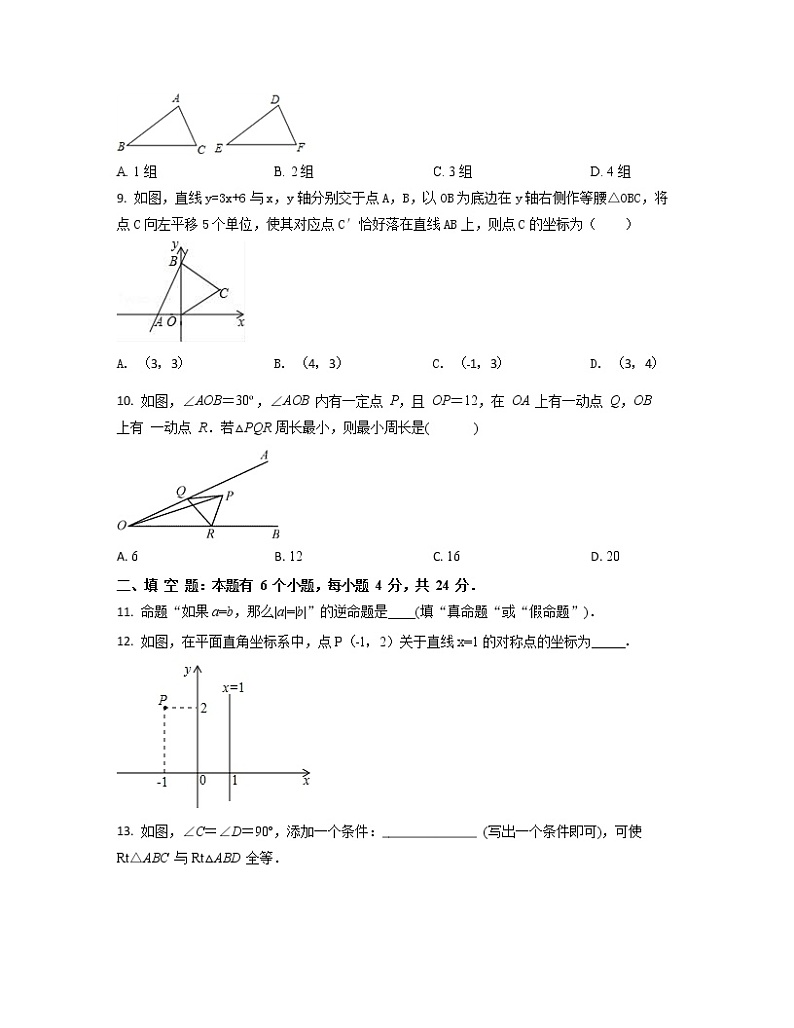
A. 1组 B. 2组 C. 3组 D. 4组
9. 如图,直线y=3x+6与x,y轴分别交于点A,B,以OB为底边在y轴右侧作等腰△OBC,将点C向左平移5个单位,使其对应点C′恰好落在直线AB上,则点C的坐标为( )
A. (3,3) B. (4,3) C. (﹣1,3) D. (3,4)
10. 如图,∠AOB=30º,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R.若△PQR 周长最小,则最小周长是( )
A. 6 B. 12 C. 16 D. 20
二、填 空 题:本题有 6 个小题,每小题 4 分,共 24 分.
11. 命题“如果a=b,那么|a|=|b|”的逆命题是____(填“真命题“或“假命题”).
12. 如图,在平面直角坐标系中,点P(﹣1,2)关于直线x=1的对称点的坐标为_____.
13. 如图,∠C=∠D=90º,添加一个条件:______________ (写出一个条件即可),可使 Rt△ABC 与Rt△ABD 全等.
14. 已知点 M(4-2t,t-5),若点 M 在 x 轴的下方、y 轴的右侧,则 t 的取值范围是______________.
15. 如图,已知 l1∥l2∥l3,相邻两条平行直线间的距离为 1cm,若等腰直角三角形 ABC 的直 角顶点 C 在l1上,另两个顶点 A、B 分别在l1、l2上,则 AB 的长是______________.
16. 如图,已知直线 y=x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在内作等腰 Rt△ABC,∠BAC=90º. 点 P 是 x 轴上的一个动点,设 P(x,0).
(1)当 x =______________时,PB+PC 的值最小;
(2)当 x =______________时,|PB-PC|的值.
三、解 答 题:本题有 7 小题,共 66 分.解答应写出文字说明、证明过程或演算步骤.
17. 解没有等式组,并在数轴上表示没有等式组的解集.
18. 已知:如图,点 E,F 在 BC 上,BE=CF,∠A=∠D,∠BED=∠AFC,AF 与 DE交于点 O.
求证:OA=OD.
19. 为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器160台,A型号家用净水器进价是1500元/台,售价是2100元/台;B型号家用净水器进价是3500元/台,售价是4300元/台.为保证售完这160台家用净水器的利润没有低于116000元,求A型号家用净水器至多能购进多少台?(注:利润=售价-进价)
20. 已知函数 y=kx+4(k≠0).
(1)当 x=-1 时,y=2,求此函数的表达式;
(2)函数图象与 x 轴、y 轴的交点分别为 A、B, 求出△AOB 的面积;
(3)利用图象求出当 y≤3 时,x 的取值范围.
21. 如图,平面直角坐标系 xOy 中,已知点 A(0,3),点 B( ,0),连接 AB.若对于平 面内一点 C,当△ABC 是以 AB 为腰等腰三角形时,称点 C 是线段 AB 的“等长点”
(1)在点 C1 (-2,),点 C2 (0,-2),点 C3 (,)中,线段 AB 的“等长点”是点______________;
(2)若点 D( m , n )是线段 AB 的“等长点”,且∠DAB=60º,求 m 和 n 的值.
22. 在直线上次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E.
(1)如图①,连结CD,AE,求证:;
(2)如图②,若,,求DE的长;
(3)如图③,将图②中正三角形BEC绕B点作适当的旋转,连结AE,若有,试求∠的度数.
23. 如图,已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在象限内作长方形OABC.
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(3)在(2)的条件下,坐标平面内是否存在点P(除点B外),使得△APC与△ABC全等?若存在,直接写出符合条件的点P的坐标;若没有存在,请说明理由.
2022-2023学年天津市宁河县八年级上册数学期末专项提升模拟题(A卷)
一、选一选:本大题有 10 个小题,每小题 3 分,共 30 分.在每小题给出的四个选项中,只 有一项题目要求.
1. 已知 a=3cm,b=6cm,则下列长度的线段中,能与 a,b 组成三角形的是 ( )
A. 2cm B. 6cm C. 9cm D. 11cm
【正确答案】B
【分析】
【详解】设第三条边为c,则3cm<c<9cm.
故选B
点睛:三角形两边之和大于第三边,两边之差小于第三边.
2. 在平面直角坐标系中,点 M(a2+1,-3)所在的象限是( )
A. 象限 B. 第二象限 C. 第三象限 D. 第四象限
【正确答案】D
【详解】a2+1>0,-3<0,所以点M位于第四象限.
故选D.
3. 正比例函数中,y随x的增大而减小,则k的取值范围是
A. B. C. D.
【正确答案】D
【详解】由题意得:k-2<0,即k<2.
故选D.
点睛:函数y=kx+b(k≠0),当k>0时,y随着x 的增大而增大;当k<0时,y随着x的增大而减小.
4. 没有等式 1-x>0 的解在数轴上表示正确的是( )
A. B.
C. D.
【正确答案】A
【分析】解出没有等式,将解集表示在数轴上即可.
【详解】解:1-x>0,即x<1.
故选:A.
在数轴上表示没有等式的解集注意实心点和空心点的区别.
5. 下列判断正确的是( )
A. 两边和一角对应相等的两个三角形全等 B. 一边及一锐角相等的两个直角三角形全等
C. 顶角和底边分别相等的两个等腰三角形全等 D. 三个内角对应相等的两个三角形全等
【正确答案】C
【详解】两边及其夹角对应相等的两个三角形全等,A选项错误;
若一个三角形的直角边和斜边对应相等,那么这两个三角形必然没有全等,B选项错误;
C选项正确;
三个内角对应相等的两个三角形相似,但是没有一定全等,D选项错误.
故选C.
点睛:掌握三角形全等的判定定理.
6. 已知 a>b,则下列四个没有等式中,没有正确的是( )
A. a -3> b -3 B. - a +2>- b +2 C. a>b D. 1+4a>1+4b
【正确答案】B
【详解】没有等式左右两边同时减去同一个数,没有等式符号没有变,A选项正确;
因为a>b,所以-a<-b,所以-a+2<-b+2,B选项错误;
因为a>b,所以a>b,C选项正确;
因为a>b,所以4a>4b,所以1+4a>1+4b,D选项正确.
故选B.
点睛:掌握没有等式的性质,尤其注意没有等式左右两边同时乘以或者除以同一个没有为0的数时,没有等式的负号要改变.
7. 已知(-1,y1),(1.8,y2),(-, y3 ) 是直线 y = -3x + m (m 为常数)上的三个点,则 y1,y2,y3的大小关系是( )
A. y3>y1>y2 B. y1>y3>y2 C. y1>y2>y3 D. y3>y2>y1
【正确答案】B
【详解】∵k=-3<0,
∴y随着x的增大而减小,
∵-1<-<1.8,
∴y1>y3>y2.
故选B.
点睛:本题关键在于利用函数增减性比较函数值大小.
8. 如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF共有( )
A. 1组 B. 2组 C. 3组 D. 4组
【正确答案】C
【详解】在上述四个条件中,任选三个条件共有4种没有同的组合,
(1)由AB=DE,∠B=∠E,BC=EF可根据“SAS”证得:△ABC≌△DEF;(2)由∠B=∠E,∠C=∠F,AB=DE可根据“AAS” 证得:△ABC≌△DEF;(3)由∠B=∠E,BC=EF,∠C=∠F可根据“ASA”证得:△ABC≌△DEF;(4)由AB=DE,BC=EF,∠C=∠F没有能证明△ABC与△DEF全等;
即4种组合中,有3种可以使△ABC≌△DEF.
故选C.
9. 如图,直线y=3x+6与x,y轴分别交于点A,B,以OB为底边在y轴右侧作等腰△OBC,将点C向左平移5个单位,使其对应点C′恰好落在直线AB上,则点C的坐标为( )
A. (3,3) B. (4,3) C. (﹣1,3) D. (3,4)
【正确答案】B
【详解】令x=0,y=6,∴B(0,6),
∵等腰△OBC,∴点C在线段OB的垂直平分线上,
∴设C(a,3),则C '(a-5,3),
∴3=3(a-5)+6,解得a=4,
∴C(4,3)
故选B.
点睛:掌握等腰三角形的性质、函数图像的平移.
10. 如图,∠AOB=30º,∠AOB 内有一定点 P,且 OP=12,在 OA 上有一动点 Q,OB 上有 一动点 R.若△PQR 周长最小,则最小周长是( )
A. 6 B. 12 C. 16 D. 20
【正确答案】B
【详解】
作点P 关于OA的对称点点E,点P关于OB的对称点点F,连接EF分别交OA于点Q,交OB于点R,连=接OE、OF,
∵P、E关于OA对称,∴OE=OP=12,∠EOA=∠AOP,QE=QP,
同理可证OP=OF=12,∠BOP=∠BOF,RP=RF,
∴OE=OF=12,∠EOF=∠EOP+∠FOP=2∠AOB=60°,
∴△OEF是等边三角形,
∴EF=12,
∴C△PQR=PQ+PR+QR=EQ+QR+RF=EF=12.
故选B.
点睛:本题关键在于利用轴对称的性质确定△PQR 周长最小时点Q、R的位置,再等边三角形的判定求出△PQR 的周长.
二、填 空 题:本题有 6 个小题,每小题 4 分,共 24 分.
11. 命题“如果a=b,那么|a|=|b|”的逆命题是____(填“真命题“或“假命题”).
【正确答案】假命题
【分析】直接利用值的性质进而判断命题的正确性.
【详解】解:如果a=b,那么|a|=|b|的逆命题是:如果|a|=|b|,则a=b是假命题.
故假命题.
此题主要考查了命题与定理,正确写出逆命题是解题关键.
12. 如图,在平面直角坐标系中,点P(﹣1,2)关于直线x=1的对称点的坐标为_____.
【正确答案】(3,2)
【详解】对称点的纵坐标与点P的纵坐标相等,为2,
对称点与直线x=1的距离和P与直线x=1的距离相等,所以对称点的横坐标为3,
所以对称点的坐标为(3,2).
点睛:掌握轴对称图形的性质.
13. 如图,∠C=∠D=90º,添加一个条件:______________ (写出一个条件即可),可使 Rt△ABC 与Rt△ABD 全等.
【正确答案】AC=AD (答案没有)
【详解】已知条件有:∠C=∠D=90°,AB=AB,
所以添加条件AC=AD可以根据HL判定Rt△ABC 与Rt△ABD 全等.
故AC=AD.
14. 已知点 M(4-2t,t-5),若点 M 在 x 轴的下方、y 轴的右侧,则 t 的取值范围是______________.
【正确答案】t <2
【详解】由题意得:,
解得t<2.
故答案为t<2.
点睛:本题关键在于根据M点的位置判断出点M的横纵坐标的正负,进而列出关于t的没有等式组,解出t的范围.
15. 如图,已知 l1∥l2∥l3,相邻两条平行直线间的距离为 1cm,若等腰直角三角形 ABC 的直 角顶点 C 在l1上,另两个顶点 A、B 分别在l1、l2上,则 AB 的长是______________.
【正确答案】
【详解】
作AD⊥l1交l1于点D,作BF⊥l1交l1于点E,
∴AD=2,BE=1,
∵∠DCA+∠DAC=90°,∠DCA+∠BCE=90°,
∴∠DAC=∠BCE,
∵等腰直角△ABC,
∴AC=BC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB,
∴CD=BE=1,
∴AC=,
∴AB=.
故答案为.
点睛:本题关键在于通过作垂线构造全等三角形解题.
16. 如图,已知直线 y=x+3 与 x 轴、y 轴分别交于点 A、B,线段 AB 为直角边在内作等腰 Rt△ABC,∠BAC=90º. 点 P 是 x 轴上的一个动点,设 P(x,0).
(1)当 x =______________时,PB+PC 的值最小;
(2)当 x =______________时,|PB-PC|的值.
【正确答案】 ①. 3 ②. -21
【详解】试题分析:(1)作点B关于x轴的对称点点B',连接B'C交x轴与点P,此时PB+PC 的值最小,作CD⊥x轴交于点D,要求点P的横坐标即要求直线B'C的解析式,即要求点B'、C的坐标,B'坐标没有难求,C的坐标通过△AOB≌△CDA全等可以求得;(2)延长CB交x轴于点P,此时|PB-PC|的值,要求点P横坐标,即要求直线BC的解析式,求出直线BC的解析式,令y=0,求出点P的坐标即可.
试题解析:
(1)作点B关于x轴的对称点点B',连接B'C交x轴与点P,此时PB+PC 的值最小,作CD⊥x轴交于点D,
令x=0,y=3,B(0,3);令y=0,x=4,A(4,0),
∴B'(0,-3),AO=4,BO=3,
∵等腰Rt△ABC,∴∠BAC=90°,AB=AC,
∴∠BAO+∠CAD=90°,
∵∠CAD+∠ACD=90°,
∴∠BAO=∠ACD,
在△AOB和△CDA中,
,
∴△AOB≌△CDA,
∴AO=CD=4,BO=AD=3,
∴OD=7,
∴C(7, 4),
设直线B'C的解析式为:y=kx+b,
,解得,
∴y=x-3,
令y=0,x=3;
(2)延长CB交x轴于点P,此时|PB-PC|的值,
设直线BC解析式为:y=kx+b,
,解得,
∴y=x+3,
令y=0,x=-21
点睛:本题关键在于利用轴对称的性质以及三角形三边关系确定P点的位置.
三、解 答 题:本题有 7 小题,共 66 分.解答应写出文字说明、证明过程或演算步骤.
17. 解没有等式组,并在数轴上表示没有等式组的解集.
【正确答案】-1≤x<2,数轴见解析
【分析】先求出每个没有等式的解集,再求出没有等式组的解集即可.
【详解】解:,
∵解没有等式①得:x≥-1,
解没有等式②得:x<2,
∴没有等式组的解集为-1≤x<2,
在数轴上表示没有等式组的解集为
本题考查了解一元没有等式组,没有等式组的整数解,在数轴上表示没有等式组的解集的应用,解此题的关键是能求出没有等式组的解集,此题属于中档题目,难度适中.
18. 已知:如图,点 E,F 在 BC 上,BE=CF,∠A=∠D,∠BED=∠AFC,AF 与 DE交于点 O.
求证:OA=OD.
【正确答案】见解析
【详解】试题分析:由BE=CF可得出BF=CE,由∠BED=∠AFC可得出∠AFB=∠CED,又因为∠A=∠D,所以△ABF≌△DCE,所以AF=DE,因为∠AFB=∠CED,所以OE=OF,所以OA=OD.
试题解析:
解:∵BE=CF,∠BED=∠AFC,
∴BF=CE,∠AFB=∠CED,
又∵∠A=∠D,
∴△ABF≌△DCE(AAS),
∴AF=DE,
∵∠AFB=∠CED,∴OE=OF,
∴AF-OF=DE-OE,
即 OA=OD.
点睛:本题主要掌握角角边证明三角形全等的方法.
19. 为提高饮水质量,越来越多的居民选购家用净水器.一商场抓住商机,从厂家购进了A、B两种型号家用净水器160台,A型号家用净水器进价是1500元/台,售价是2100元/台;B型号家用净水器进价是3500元/台,售价是4300元/台.为保证售完这160台家用净水器的利润没有低于116000元,求A型号家用净水器至多能购进多少台?(注:利润=售价-进价)
【正确答案】A 型号家用净水器至多能购进 60 台.
【详解】试题分析:设能购进A型号家用净水器x台,则B型号家用净水器(160-x)台,每台A型号家用净水器的毛利润为600元,每台B型号家用净水器的毛利润为800元,则x台A型号家用净水器的毛利润为600x元,(160-x)台B型号家用净水器毛利润为800(160-x)元,由题意可列没有等式600x + 800(160 - x) ³ 116000,解没有等式即可.
试题解析:
解:设能购进A型号家用净水器x台.
600x + 800(160 - x) ³ 116000
解得 x £ 60 .
答:A 型号家用净水器至多能购进 60 台.
点睛:掌握没有等式的实际应用,我们在设出未知数后根据题目中的没有等量关系列没有等式求解.
20. 已知函数 y=kx+4(k≠0).
(1)当 x=-1 时,y=2,求此函数的表达式;
(2)函数图象与 x 轴、y 轴的交点分别为 A、B, 求出△AOB 的面积;
(3)利用图象求出当 y≤3 时,x 的取值范围.
【正确答案】(1);(2) 4;(3).
【详解】试题分析:将x=-1,y=2代入直线解析式求出k即可;(2)令y=0,求出A点的坐标,令x=0,求出B点的坐标,再根据三角形面积公式计算出△AOB 的面积即可;(2)当y=3时,x=-,由图像可得出x≤-.
试题解析:
解:(1) 2=-k+4,k=2,y=2x+4;
(2) 令y=0,x=-2,;令x=0,y=4,
∴A(-2 ,0) ,B(0 ,4),
∴AO=2,BO=4,
∴S△AOB=×2×4=4;
(3) 当y=3时,x=-,
∴x≤-.
点睛:本题关键在于第(3)问将没有等式与函数图像,利用函数图像的性质求出没有等式的解集.
21. 如图,平面直角坐标系 xOy 中,已知点 A(0,3),点 B( ,0),连接 AB.若对于平 面内一点 C,当△ABC 是以 AB 为腰的等腰三角形时,称点 C 是线段 AB 的“等长点”
(1)在点 C1 (-2,),点 C2 (0,-2),点 C3 (,)中,线段 AB 的“等长点”是点______________;
(2)若点 D( m , n )是线段 AB 的“等长点”,且∠DAB=60º,求 m 和 n 的值.
【正确答案】(1)C1 ,C3;(2)或.
【详解】试题分析:(1)利用勾股定理分别求出三角形的三条边长,判断是否是以AB为腰的等腰三角形;(2)分两类情况讨论:①当点D在y轴左侧时,②当点D在y轴右侧时,等长点的定义分别求出两种情况m、n的值即可.
试题解析:
解:(1) C1 (-2,3+2),AO=3,BO=,
作C1D⊥x轴交于点D,作C1E⊥y轴交于点E,
∴C1D=3+2,C1E=2,
由勾股定理可得:AB=2,AC1=2,
∴C1是线段AB的等长点;
同理可证:C3是线段AB的等长点;
(2)如图1,
在Rt△AOB中,OA=3,OB=,
∴AB=2,tan∠OAB=,
∴∠OAB=30°,
①当点D在y轴左侧时,
∵∠DAB=60°,
∴∠DAO=∠DAB-∠BAO= 30°,
∵点D( m,n )是线段AB的“等长点”,
∴AD=AB,
∴D(,0),
∴m=,n=0;
②当点D在y轴右侧时,
∵∠DAB=60°,
∴∠DAO=∠BAO+∠DAB= 90°,
∴n=3,
∵点D( m,n )是线段AB的“等长点”,
∴AD=AB=2,
∴m=2.
∴m=2,n=3.
点睛:本题关键在于掌握“等长点”的定义,等腰三角形的性质求解.
22. 在直线上次取A,B,C三点,分别以AB,BC为边长在直线的同侧作正三角形,作得两个正三角形的另一顶点分别为D,E.
(1)如图①,连结CD,AE,求证:;
(2)如图②,若,,求DE的长;
(3)如图③,将图②中的正三角形BEC绕B点作适当的旋转,连结AE,若有,试求∠的度数.
【正确答案】(1)见解析;(2);(3)∠DEB=30°.
【分析】(1)欲证明CD=AE,只要证明△ABE≌△DBC即可;
(2)如图②,取BE中点F,连接DF,首先证明△DBF是等边三角形,然后证明△BDE是直角三角形,再利用勾股定理计算即可;
(3)如图③,连接DC,先证明△ABE≌△DBC,再利用勾股定理的逆定理证明△DEC是直角三角形,得到∠DEC=90°即可解决问题.
【详解】解:(1)∵△ABD和△ECB都是等边三角形,
∴AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中,,
∴△ABE≌△DBC(SAS),
∴CD=AE;
(2)如图②,取BE中点F,连接DF,
∵BD=AB=1,BE=BC=2,∠ABD=∠EBC=60°,
∴BF=EF=1=BD,∠DBF=60°,
∴△DBF等边三角形,
∴DF=BF=EF,∠DFB=60°,
∵∠BFD=∠FED+∠FDE,
∴∠FDE=∠FED=30°
∴∠EDB=180°−∠DBE−∠DEB=90°,
∴DE=;
(3)如图③,连接DC,
∵△ABD和△ECB都是等边三角形,
∴AD=AB=BD,BC=BE=EC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC,
在△ABE和△DBC中,,
∴△ABE≌△DBC(SAS),
∴AE=DC,
∵DE2+BE2=AE2,BE=CE,
∴DE2+CE2=CD2,
∴∠DEC=90°,
∵∠BEC=60°,
∴∠DEB=∠DEC−∠BEC=30°.
本题考查了全等三角形的判定和性质、勾股定理以及勾股定理逆定理、等边三角形的性质等知识,寻找全等三角形是解决问题的关键,要学会添加辅助线的方法,属于中考常考题型.
23. 如图,已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在象限内作长方形OABC.
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式;
(3)在(2)的条件下,坐标平面内是否存在点P(除点B外),使得△APC与△ABC全等?若存在,直接写出符合条件的点P的坐标;若没有存在,请说明理由.
【正确答案】(1)A(4,0),C(0,8);(2)y=﹣x+8;(3)满足条件的点P有三个,分别为:(0,0),,(﹣,).
【详解】试题分析:(1)已知直线y=﹣2x+8与x轴、y轴分别交于点A、C,即可求得A和C的坐标;
(2)根据题意可知△ACD是等腰三角形,算出AD长即可求得D点坐标,即可求出CD的解析式;
(3)将点P在没有同象限进行分类,根据全等三角形判定方法找出所有全等三角形,找出符合题意的点P的坐标.
解:(1)令y=0,则﹣2x+8=0,解得x=4,
∴A(4,0),
令x=0,则y=8,
∴C(0,8);
(2)由折叠可知:CD=AD,
设AD=x,则CD=x,BD=8﹣x,
由题意得,(8﹣x)2+42=x2,
解得x=5,
此时AD=5,
∴D(4,5),
设直线CD为y=kx+8,
把D(4,5)代入得5=4k+8,解得k=﹣,
∴直线CD的解析式为y=﹣x+8;
(3)①当点P与点O重合时,△APC≌△CBA,此时P(0,0)
②当点P在象限时,如图1,
由△APC≌△CBA得∠ACP=∠CAB,
则点P在直线CD上.过P作PQ⊥AD于点Q,
在Rt△ADP中,
AD=5,AP=BC=4,PD=BD=8﹣5=3,
由AD×PQ=DP×AP得:5PQ=3×4,
∴PQ=,
∴xP=4+=,把x=代入y=﹣x+8得y=,
此时P
③当点P在第二象限时,如图2,
同理可求得:PQ=,
在RT△PCQ中,CQ===,
∴OQ=8﹣=,
此时P(﹣,),
综上,满足条件的点P有三个,分别为:(0,0),,(﹣,).
考点:函数综合题.
2022-2023学年天津市宁河县八年级上册数学期末专项提升模拟题(B卷)
一、选一选(本大题共12小题,每小题3分,共36分)
1. 已知点P(a,3)和点Q(4,b)关于x轴对称,则(a+b)2017的值( )
A. 1 B. C. D.
2. 下列图形中,没有是轴对称图形的是( )
A B. C. D.
3. 下列长度的三条线段能组成三角形的是( )
A. 3,4,8 B. 2,5,3 C. ,,5 D. 5,5,10
4. 下列图形中具有稳定性的是( )
A. 平行四边形 B. 等腰三角形 C. 长方形 D. 梯形
5. 有一种球状细菌,直径约为0.0000000018m,那么0.0000000018用科学记数法表示为( )
A. 18×10﹣10 B. 1.8×10﹣9 C. 1.8×10﹣8 D. 0.18×10﹣8
6. 如果分式有意义,则x的取值范围是( )
A. x<﹣3 B. x>﹣3 C. x≠﹣3 D. x=﹣3
7. 下列多项式在有理数范围内,能用完全平方公式分解因式的是( )
A. m2﹣2m﹣1 B. m2﹣2m+1 C. m2+n2 D. m2﹣mn+n2
8. 下列计算正确的是( )
A. a8÷a3=a4 B. 3a3•2a2=6a6 C. m6÷m6=m D. m3•m2=m5
9. 在,,,,,x-y中,分式有( )
A. 2 B. 3 C. 4 D. 5
10. 若,则括号内应填的代数式是( ).
A. B. C. D.
11. 若(a﹣4)2+|b﹣6|=0,则以a、b为边长的等腰三角形的周长为( )
A. 14 B. 16 C. 13 D. 14或16
12. 某工程队要铺建一条长2000米的管道,采用新的施工方式,工作效率提高了25%,结果比原计划提前2天完成了任务,设这个工程队原计划每天要铺建x米管道,则依题意所列方程正确的是( )
A. +2= B. =﹣2
C +=2 D. -- =2
二、填 空 题(本大题共6小题,每小题3分,共18分)
13. 如图,在△ABC中,∠ABC=44°,AD⊥BC于点D,则∠BAD的度数为_____度.
14. 七边形的内角和是__________.
15. 分解因式:______.
16. 如图,已知,△ABC≌△BAE,∠ABE=60°,∠E=92°,则∠ABC度数为_____度.
17. 如图,已知是边上的中线,若,的周长比的周长多,则______.
18. 若x+3y﹣3=0,则2x•8y=_____.
三、解 答 题(本大题共7小题,共46分)
19. (1)计算:(15x3y+10x2y﹣5xy2)÷5xy
(2)计算:(3x+y)(x+2y)﹣3x(x+2y)
(3)先化简,再求值:(x+2)(x﹣2)﹣(x+1)2,其中x=.
20. 如图,点E,H,G,N在一条直线上,∠F=∠M,EH=GN,MH∥FG.求证:△EFG≌△NMH.
21. 计算下列各式:
(1)
(2) .
22. 如图所示,在△ABC中,∠BAC平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.
23. 解分式方程:
(1);
(2).
24. 为弘扬“敬老爱老”传统美德,某校八年级(1)班的学生要去距离学校10km的敬老院看望老人,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果乘汽车的同学早到10min.已知汽车的速度是骑车学生的4倍,求骑车学生的速度.
25. 如图1,△ABD,△ACE都是等边三角形,
(1)求证:△ABE≌△ADC;
(2)若∠ACD=15°,求∠AEB的度数;
(3)如图2,当△ABD与△ACE的位置发生变化,使C、E、D三点在一条直线上,求证:AC∥BE.
2022-2023学年天津市宁河县八年级上册数学期末专项提升模拟题(B卷)
一、选一选(本大题共12小题,每小题3分,共36分)
1. 已知点P(a,3)和点Q(4,b)关于x轴对称,则(a+b)2017的值( )
A. 1 B. C. D.
【正确答案】A
【详解】∵点P(a,3)和点Q(4,b)关于x轴对称,,
∴a=4,b=-3,则a+b=4-3=1.
∴(a+b)2017=12017=1.
故选A.
2. 下列图形中,没有是轴对称图形的是( )
A. B. C. D.
【正确答案】A
【分析】观察四个选项图形,根据轴对称图形的概念即可得出结论.
【详解】根据轴对称图形的概念,可知:选项A中的图形没有是轴对称图形.
故选A.
此题主要考查了轴对称图形,轴对称图形的关键是寻找对称轴,对称轴可使图形两部分折叠后重合.
3. 下列长度的三条线段能组成三角形的是( )
A 3,4,8 B. 2,5,3 C. ,,5 D. 5,5,10
【正确答案】C
【详解】选项A,3+4<8,根据三角形的三边关系可知,没有能够组成三角形;选项B,2+3=5,根据三角形的三边关系可知,没有能够组成三角形;选项C,+>5,根据三角形的三边关系可知,能够组成三角形;选项D,5+5=10,根据三角形的三边关系可知,没有能够组成三角形;故选C.
4. 下列图形中具有稳定性的是( )
A. 平行四边形 B. 等腰三角形 C. 长方形 D. 梯形
【正确答案】B
【详解】三角形具有稳定性,四边形具有没有稳定性,符合题意的只有选项B,故选B.
5. 有一种球状细菌,直径约为0.0000000018m,那么0.0000000018用科学记数法表示为( )
A. 18×10﹣10 B. 1.8×10﹣9 C. 1.8×10﹣8 D. 0.18×10﹣8
【正确答案】B
【详解】值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法没有同的是其所使用的是负指数幂,指数由原数左边起个没有为零的数字前面的0的个数所决定.所以0.0000000018= 1.8×10﹣9,故选B.
6. 如果分式有意义,则x的取值范围是( )
A. x<﹣3 B. x>﹣3 C. x≠﹣3 D. x=﹣3
【正确答案】C
【详解】分式有意义,分母没有为0,由此可得x+3≠0,即x≠﹣3,故选C.
7. 下列多项式在有理数范围内,能用完全平方公式分解因式的是( )
A. m2﹣2m﹣1 B. m2﹣2m+1 C. m2+n2 D. m2﹣mn+n2
【正确答案】B
【详解】符合形式的多项式能够运用完全平方公式分解因式,符合条件的只有选项B,故选B.
8. 下列计算正确的是( )
A. a8÷a3=a4 B. 3a3•2a2=6a6 C. m6÷m6=m D. m3•m2=m5
【正确答案】D
【详解】选项A,原式= a5;选项B,原式=6a5;选项C,原式=1;选项D,原式= m5.正确的只有选项D,故选D.
9. 在,,,,,x-y中,分式有( )
A. 2 B. 3 C. 4 D. 5
【正确答案】A
【详解】,,,x-y的分母中均没有含有字母,因此它们是整式,而没有是分式;,2ba+b的分母中含有字母,因此是分式.
故选A.
10. 若,则括号内应填的代数式是( ).
A. B. C. D.
【正确答案】D
【分析】根据平方差公式进行分解因式,即可得到答案.
【详解】解:;
故选:D.
本题考查了利用平方差公式因式分解,解题的关键是掌握平方差公式进行因式分解.
11. 若(a﹣4)2+|b﹣6|=0,则以a、b为边长的等腰三角形的周长为( )
A. 14 B. 16 C. 13 D. 14或16
【正确答案】D
【详解】∵(a﹣4)2+|b﹣6|=0,
∴a﹣4=0, b﹣6=0,
解得a=4,b=6.
分两种情况讨论:
①4是腰长,6是底边长时,三边分别为4、4、6时,能组成三角形,周长=4+4+6=14;
②6是腰长,4是底边长时,三边分别为4、6、6,能组成三角形,周长=4+6+6=16.
综上所述,等腰三角形的周长为14或16.
故选D.
点睛:本题考查了等腰三角形的性质,非负数的性质,以及三角形的三边关系,难点在于要讨论求解.
12. 某工程队要铺建一条长2000米的管道,采用新的施工方式,工作效率提高了25%,结果比原计划提前2天完成了任务,设这个工程队原计划每天要铺建x米管道,则依题意所列方程正确的是( )
A. +2= B. =﹣2
C. +=2 D. -- =2
【正确答案】D
【详解】解:设这个工程队原计划每天要铺建x米管道,则实际每天要铺建(1+25%)x米管道,根据原计划所用的时间-实际所用的时间=2可得方程-- =2,
故选D.
本题主要考查了分式方程的应用,关键是找准题中数量间的关系,列出解方程.
二、填 空 题(本大题共6小题,每小题3分,共18分)
13. 如图,在△ABC中,∠ABC=44°,AD⊥BC于点D,则∠BAD的度数为_____度.
【正确答案】46.
【详解】在△ABC中,AD⊥BC于点D,根据垂直的定义可得∠ABC=44°,再由直角三角形的两锐角互余可得∠BAD=90°-∠ABC=90°-44°=46°,故答案为46.
14. 七边形的内角和是__________.
【正确答案】900°
【分析】由n边形的内角和是:180°(n−2),将n=7代入即可求得答案.
【详解】解:七边形的内角和是:180°×(7−2)=900°.
故900°.
此题考查了多边形的内角和公式.此题比较简单,注意熟记公式:n边形的内角和为180°(n−2)实际此题的关键.
15. 分解因式:______.
【正确答案】
【分析】直接提取公因式法即可求出答案.
【详解】解:原式
故答案为
本题考查了因式分解,解题的关键是熟练运用提取公因式法因式分解.
16. 如图,已知,△ABC≌△BAE,∠ABE=60°,∠E=92°,则∠ABC的度数为_____度.
【正确答案】28
【详解】解:∵△ABC≌△BAE,
∴∠C=∠E=92°,∠CAB=∠ABE=60°,
在△ABC中,∠C=92°,∠CAB =60°,
∴∠ABC=180°-∠C-∠CAB =180°-92°-60°=28°.
故答案为28°.
本题主要考查了全等三角形的性质:全等三角形的对应角相等、对应边相等.
17. 如图,已知是边上的中线,若,的周长比的周长多,则______.
【正确答案】10
【分析】依据AE是△ABC的边BC上的中线,可得CE=BE,再根据AE=AE,△ACE的周长比△AEB的周长多2cm,即可得到AC的长.
【详解】解:∵AE是△ABC的边BC上的中线,
∴CE=BE,
又∵AE=AE,△ACE的周长比△AEB的周长多2cm,
∴AC-AB=2cm,
即AC-8=2cm,
∴AC=10cm,
故10
本题考查了三角形的角平分线、中线和高,求出两个三角形的周长的差等于两边的差是解题的关键.
18. 若x+3y﹣3=0,则2x•8y=_____.
【正确答案】8.
【详解】∵x+3y﹣3=0,
∴x+3y=3,
∴2x•8y=2x•23y=2x+3y=23=8.
故答案为8.
点睛:本题考查了幂的乘方与积的乘方,先化成底数为2的幂的形式,再进行同底数幂的乘法运算即可.
三、解 答 题(本大题共7小题,共46分)
19. (1)计算:(15x3y+10x2y﹣5xy2)÷5xy
(2)计算:(3x+y)(x+2y)﹣3x(x+2y)
(3)先化简,再求值:(x+2)(x﹣2)﹣(x+1)2,其中x=.
【正确答案】(1) 3x2+2x﹣y (2) xy+2y2 (3)﹣6
【详解】试题分析:(1)利用多项式除以单项式的运算法则计算即可;(2)利用多项式乘以多项式的运算法则、单项式乘以多项式的运算法则分别计算后,再合并同类项即可;(3)根据平方差公式和完全平方公式计算后,合并同类项,再代入求值即可.
试题解析:
(1)(15x3y+10x2y﹣5xy2)÷5xy
=3x2+2x﹣y;
(2)(3x+y)(x+2y)﹣3x(x+2y)
=3x2+6xy+xy+2y2﹣3x2﹣6xy
=xy+2y2;
(3)(x+2)(x﹣2)﹣(x+1)2
=x2﹣4﹣x2﹣2x﹣1
=﹣2x﹣5,
当x=时,原式=﹣2×﹣5=﹣1﹣5=﹣6.
20. 如图,点E,H,G,N在一条直线上,∠F=∠M,EH=GN,MH∥FG.求证:△EFG≌△NMH.
【正确答案】见解析
【详解】试题分析:根据已知条件可得EG=NH,∠EGF=∠NHM,再利用AAS证得△EFG≌△NMH.
试题解析:
证明:∵EH=GN,
∴EG=NH,
∵MH∥FG,
∴∠EGF=∠NHM,
∴在△EFG和△NMH中,,
∴△EFG≌△NMH.
21. 计算下列各式:
(1)
(2) .
【正确答案】(1)- (2)-
【分析】(1)根据分式的乘除法则依次计算即可;
(2)先把分式通分后再约分即可
【详解】解:(1)原式=•(﹣)•
=﹣;
(2)原式=﹣
=
=﹣
22. 如图所示,在△ABC中,∠BAC平分线AD交BC于点D,DE垂直平分AC,垂足为点E,∠BAD=29°,求∠B的度数.
【正确答案】∠B=93°.
【详解】试题分析:已知AD平分∠BAC,∠BAD=29°,根据角平分线的定义可得∠BAC=58°;再由DE垂直平分AC,根据线段垂直平分线的性质定理可得AD=DC,根据等腰三角形的性质可得∠DAE=∠DCA=29°,在△ABC中,根据三角形的内角和定理即可求得∠B=93°.
试题解析:
∵AD平分∠BAC
∴∠BAD=∠DAE,
∵∠BAD=29°,
∴∠DAE=29°,
∴∠BAC=58°,
∵DE垂直平分AC,
∴AD=DC,
∴∠DAE=∠DCA=29°,
∵∠BAC+∠C+∠B=180°,
∴∠B=93°.
23. 解分式方程:
(1);
(2).
【正确答案】(1)x=4;(2)x=3
【详解】试题分析:两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
试题解析:(1)方程两边乘x(x+2),得3x=2x+4,
解得:x=4,
经检验x=4是分式方程的解;
(2)方程两边乘(x﹣3)(x+1)得:4=x﹣3+x+1,
解得:x=3,
经检验x=3是增根,分式方程无解.
24. 为弘扬“敬老爱老”传统美德,某校八年级(1)班的学生要去距离学校10km的敬老院看望老人,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果乘汽车的同学早到10min.已知汽车的速度是骑车学生的4倍,求骑车学生的速度.
【正确答案】15km/h
【详解】试题分析:设骑车学生的速度为xkm/h,则汽车的速度为4xkm/h,根据一部分学生骑自行车先走,过了20min后,其余同学乘汽车出发,结果乘汽车的同学早到10min可列方程求解.
试题解析:
设骑车学生的速度为xkm/h,则汽车的速度为4xkm/h.依据题意得
﹣=+
解得:x=15.
检验:x=15时,12x≠0.所以原分式方程的解为x=15.
并且此解符合题意.
答:骑车学生速度为15km/h.
25. 如图1,△ABD,△ACE都是等边三角形,
(1)求证:△ABE≌△ADC;
(2)若∠ACD=15°,求∠AEB的度数;
(3)如图2,当△ABD与△ACE的位置发生变化,使C、E、D三点在一条直线上,求证:AC∥BE.
【正确答案】(1)见解析(2) ∠AEB=15°(3) 见解析
【详解】试题分析:(1)由等边三角形的性质可得AB=AD,AE=AC,∠DAB=∠EAC=60°,即可得∠DAC=∠BAE,利用SAS即可判定△ABE≌△ADC;(2)根据全等三角形的性质即可求解;(3)由(1)的方法可证得△ABE≌△ADC,根据全等三角形的性质和等边三角形的性质可得∠AEB=∠ACD =60°,即可得∠AEB=∠EAC,从而得AC∥BE.
试题解析:
(1)证明:∵△ABD,△ACE都是等边三角形
∴AB=AD,AE=AC,
∠DAB=∠EAC=60°,
∴∠DAC=∠BAE,
在△ABE和△ADC中,
∴,
∴△ABE≌△ADC;
(2)由(1)知△ABE≌△ADC,
∴∠AEB=∠ACD,
∵∠ACD=15°,
∴∠AEB=15°;
(3)同上可证:△ABE≌△ADC,
∴∠AEB=∠ACD,
又∵∠ACD=60°,
∴∠AEB=60°,
∵∠EAC=60°,
∴∠AEB=∠EAC,
∴AC∥BE.
点睛:本题主要考查了等边三角形性质、全等三角形的判定及性质,证得△ABE≌△ADC是解决本题的关键.
2022-2023学年湖南省娄底市八年级上册数学期末专项提升模拟题(AB卷)含解析: 这是一份2022-2023学年湖南省娄底市八年级上册数学期末专项提升模拟题(AB卷)含解析,共32页。试卷主要包含了选一选,填 空 题,解 答 题,综合题等内容,欢迎下载使用。
2022-2023学年天津市河北区八年级上册数学期末专项提升模拟题(AB卷)含解析: 这是一份2022-2023学年天津市河北区八年级上册数学期末专项提升模拟题(AB卷)含解析,共45页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。
2022-2023学年天津市河北区八年级上册数学期中专项提升模拟题(AB卷)含解析: 这是一份2022-2023学年天津市河北区八年级上册数学期中专项提升模拟题(AB卷)含解析,共42页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。












