2022-2023学年天津市河北区八年级下册数学期末专项提升模拟题（AB卷）含解析

这是一份2022-2023学年天津市河北区八年级下册数学期末专项提升模拟题（AB卷）含解析，共46页。试卷主要包含了选一选，四象限B. 等内容，欢迎下载使用。
2022-2023学年天津市河北区八年级下册数学期末专项提升模拟题（A卷）
一、选一选（本大题共12小题，共36.0分）
1. 下列各式中，运算正确的是（　　）
A. ＝﹣2 B. +＝ C. ×＝4 D. 2﹣
2. 下列四组线段中，能组成直角三角形的是（ ）
A. a=1，b=2，c=3 B. a=2，b=3，c=4
C. a=2，b=4，c=5 D. a=3，b=4，c=5
3. 函数y=2x﹣5的图象（　　）
A. 、三、四象限 B. 、二、四象限
C. 第二、三、四象限 D. 、二、三象限
4. 关于数据－4，1，2，－1，2，下面结果中，错误是( )
A. 中位数为1 B. 方差为26 C. 众数为2 D. 平均数为0
5. 要得到函数y=2x+3的图象，只需将函数y=2x的图象（ ）
A. 向左平移3个单位 B. 向右平移3个单位
C. 向下平移3个单位 D. 向上平移3个单位
6. 如图，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD=120°，AB=2，则AC的长为( )

A 2 B. 4 C. 6 D. 8
7. 已知是函数的图象上的两个点，则的大小关系是（ ）
A. B. C. D. 没有能确定
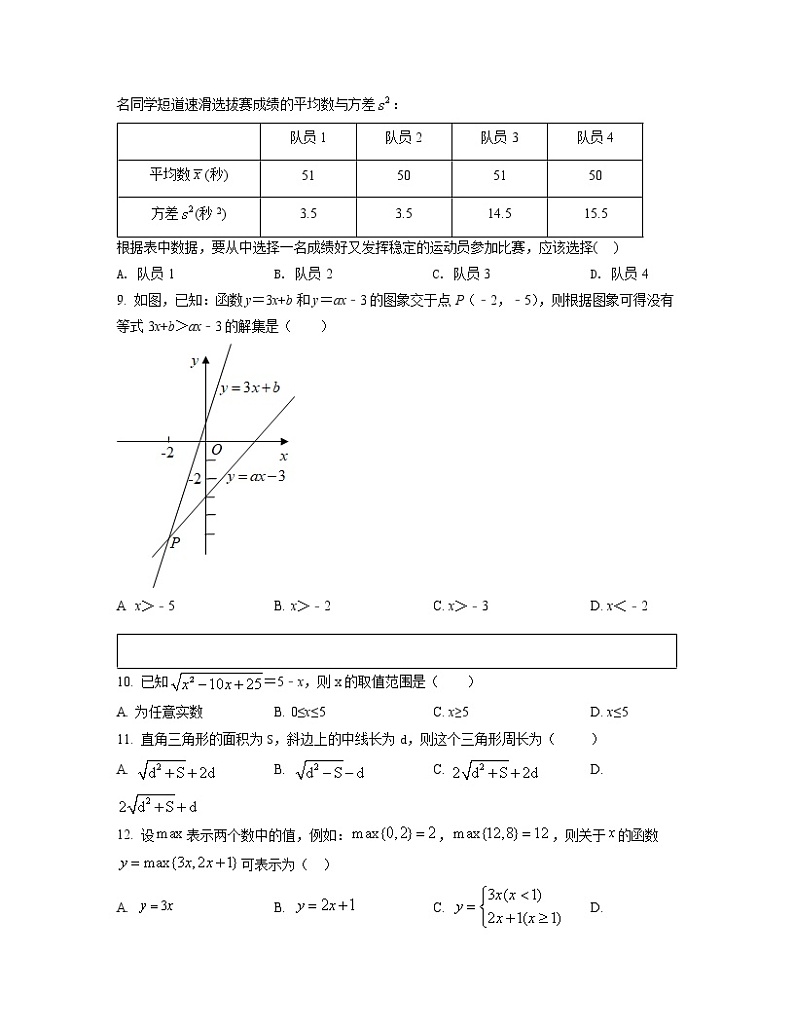
8. 2022年将在北京-张家口举办冬季奥运会，很多学校开设了相关的课程．如表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差：

队员1
队员2
队员3
队员4
平均数(秒)
51
50
51
50
方差(秒2)
3.5
3.5
14.5
15.5
根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择( )
A. 队员1 B. 队员2 C. 队员3 D. 队员4
9. 如图，已知：函数y＝3x+b和y＝ax﹣3的图象交于点P（﹣2，﹣5），则根据图象可得没有等式3x+b＞ax﹣3的解集是（　　）

A x＞﹣5 B. x＞﹣2 C. x＞﹣3 D. x＜﹣2

10. 已知＝5﹣x，则x的取值范围是（　　）
A. 为任意实数 B. 0≤x≤5 C. x≥5 D. x≤5
11. 直角三角形的面积为S，斜边上的中线长为d，则这个三角形周长为（ ）
A. B. C. D.
12. 设表示两个数中的值，例如：，，则关于的函数可表示为（ ）
A. B. C. D.
二、填 空 题（本大题共6小题，共18.0分）
13. 若在实数范围内有意义，则x的取值范围是______．
14. 已知一组数据，，，，的平均数是2，那么另一组数据，，，，的平均数是______．
15. 计算=__________．
16. 如图，两张等宽的纸条交叉叠放在一起，若重合部分构成的四边形中，，，则的长为_______________．


17. 已知函数与图象如图所示，则下列结论：①；②；③关于的方程的解为；④当，.其中正确的有_______(填序号)．

18. 一般地，在平面直角坐标系中，我们求点到直线间的距离，可用下面的公式求解：
点到直线的距离公式是：
如：求：点到直线的距离．
解：由点到直线的距离公式，得
根据平行线的性质，我们利用点到直线的距离公式，也可以求两平行线间的距离．
则两条平行线：和：间的距离是______．
三、解 答 题
19. 计算：
20. 如图所示的一块地，已知，，，，，求这块地的面积．

21. 我市某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如图所示．

（1）根据图示填写下表；


平均数（分）
中位数（分）
众数（分）
初中部

85

高中部
85

100
（2）两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
22. 如图，函数与正比例函数的图象交于点．

（1）求正比例函数和函数的解析式；
（2）根据图象，写出关于的没有等式的解集；
（3）求的面积．
23. 如图，矩形ABCD对角线AC、BD交于点O，且DE∥AC，CE∥BD．
(1)求证：四边形OCED菱形；
(2)若∠BAC=30°，AC=4，求菱形OCED的面积．


24. 已知：甲乙两车分别从相距300千米的A、B两地同时出发相向而行，其中甲到达B地后立即返回，如图是它们离各自出发地的距离y（千米）与行驶时间x（小时）之间的函数图象．


（1）求甲车离出发地的距离y甲（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；
（2）它们出发小时时，离各自出发地的距离相等，求乙车离出发地的距离y乙（千米）与行驶时间x（小时）之间的函数关系式，并写出自变量的取值范围；
（3）在（2）的条件下，求它们在行驶的过程中相遇的时间．
25. 现有正方形ABCD和一个以O为直角顶点的三角板，移动三角板，使三角板两直角边所在直线分别与直线BC、CD交于点M、N．
（1）如图1，若点O与点A重合，则OM与ON的数量关系是　 　；
（2）如图2，若点O在正方形的（即两对角线交点），则（1）中的结论是否仍然成立？请说明理由；
（3）如图3，若点O在正方形的内部（含边界），当OM=ON时，请探究点O在移动过程中可形成什么图形？
（4）如图4，是点O在正方形外部的一种情况．当OM=ON时，请你就“点O的位置在各种情况下（含外部）移动所形成的图形”提出一个正确的结论．（没有必说明）












2022-2023学年天津市河北区八年级下册数学期末专项提升模拟题（A卷）
一、选一选（本大题共12小题，共36.0分）
1. 下列各式中，运算正确的是（　　）
A. ＝﹣2 B. +＝ C. ×＝4 D. 2﹣
【正确答案】C

【分析】根据二次根式的性质对A进行判断；根据二次根式的加减法法则对B、D进行判断；根据二次根式的乘法法则对C进行判断．
【详解】解：A、＝2，故原题计算错误；
B、+＝+2＝3，故原题计算错误；
C、＝＝4，故原题计算正确；
D、2和没有能合并，故原题计算错误；
故选：C
此题主要考查了二次根式的运算及性质，熟练掌握二次根式的性质及加减法运算法则是解题关键．
2. 下列四组线段中，能组成直角三角形的是（ ）
A. a=1，b=2，c=3 B. a=2，b=3，c=4
C. a=2，b=4，c=5 D. a=3，b=4，c=5
【正确答案】D

【分析】由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
【详解】解：A．∵ 12+22=5≠32 ，
∴没有能构成直角三角形，故本选项错误；
B．∵ 22+32=13≠42 ，
∴没有能构成直角三角形，故本选项错误；
C．∵ 22+42=20≠52 ，
∴没有能构成直角三角形，故本选项错误；
D．∵ 32+42=25=52 ，
∴能构成直角三角形，故本选项正确．
故选D．
本题考查了勾股定理的逆定理．解题的关键是，验证两小边的平方和等于最长边的平方即可证明直角三角形．
3. 函数y=2x﹣5图象（　　）
A. 、三、四象限 B. 、二、四象限
C. 第二、三、四象限 D. 、二、三象限
【正确答案】A

【分析】先根据函数的性质判断出此函数图象所的象限，再进行解答即可．
【详解】∵函数y=2x-5中，k=2＞0，
∴此函数图象一、三象限，
∵b= -5＜0，
∴此函数图象与y轴负半轴相交，
∴此函数的图象一、三、四象限，没有第二象限．
故选A．
本题考查的是函数的性质，即函数y=kx+b（k≠0）中，当k＞0时，函数图象一、三象限，当b＜0时，（0，b）在y轴的负半轴，直线与y轴交于负半轴．
4. 关于数据－4，1，2，－1，2，下面结果中，错误的是( )
A. 中位数为1 B. 方差为26 C. 众数为2 D. 平均数为0
【正确答案】B

【详解】A．从小到大排序为-4，-1，1，2，2，中位数为1，故正确；
B． ，
，故没有正确；
C．众数是2，故正确；
D．，故正确；
故选B．
5. 要得到函数y=2x+3的图象，只需将函数y=2x的图象（ ）
A. 向左平移3个单位 B. 向右平移3个单位
C. 向下平移3个单位 D. 向上平移3个单位
【正确答案】D

【分析】平移后相当于x没有变y增加了3个单位，由此可得出答案．
【详解】解：由题意得x值没有变y增加3个单位
∴应向上平移3个单位．
故选：D．
本题考查函数图象的平移，熟练掌握函数平移的坐标规律是解题关键．
6. 如图，在矩形ABCD中，对角线AC，BD交于点O，已知∠AOD=120°，AB=2，则AC的长为( )

A. 2 B. 4 C. 6 D. 8
【正确答案】B

【分析】已知四边形ABCD是矩形，∠AOD=120°，AB=2，根据矩形的性质可证得△AOB是等边三角形，则OA=OB=AB=2，AC=2OA=4．
【详解】解：∵四边形ABCD是矩形，
∴AC=BD，OA=OC，OB=OD，
∴OA=OB，
∵∠AOD=120°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴OA=OB=AB=2，
∴AC=2OA=4，
故选：B．
本题考查了矩形的基本性质，解题的关键是掌握等边三角形的判定和性质．
7. 已知是函数的图象上的两个点，则的大小关系是（ ）
A. B. C. D. 没有能确定
【正确答案】C

【分析】根据是函数y=-x-1的图象上的两个点，由-3