2022-2023学年湖南省长沙市八年级下册数学期中专项提升模拟（AB卷）含解析

这是一份2022-2023学年湖南省长沙市八年级下册数学期中专项提升模拟（AB卷）含解析，共43页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。
2022-2023学年湖南省长沙市八年级下册数学期中专项提升模拟
（A卷）
一、选一选（每小题3分，共30分）
1. 下列二次根式中，最简二次根式的是（　　）
A. B. C. D.
2. 下列以线段a、b、c的长为边的三角形中，没有能构成直角三角形的是（ ）
A. B.
C. D.
3. 如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于AB的长为半径画弧，两弧相交于C、D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（ ）

A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形
4. 下列各式计算正确的是（　　）
A. B. C. D.
5. 直角三角形两个直角边长分别是3、4，则这个直角三角形的第三边是（ ）
A. 5 B. C. 5或 D. 无法确定
6. 如图，在周长为20cm的平行四边形ABCD中，AB≠AD，AC和BD相交于点O，OE⊥BD交AD于E，则ΔABE的周长为（ ）

A. 4cm B. 6cm C. 8cm D. 10cm
7. 当1＜a＜2时，代数式＋|1－a|的值是( )
A. －1 B. 1 C. 2a－3 D. 3－2a
8. 将一根24cm的筷子，置于底面直径为15cm，高8cm的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度hcm，则h的取值范围是（　　）

A h≤17cm B. h≥8cm
C. 15cm≤h≤16cm D. 7cm≤h≤16cm
9. 如图，点P是矩形ABCD的边AD上的一动点，矩形的两条边AB、BC的长分别是6和8，则点P到矩形的两条对角线AC和BD的距离之和是（ ）

A. 4.8 B. 5 C. 6 D. 7.2
10. 如图，将边长为12cm的正方形ABCD折叠，使得点A落在CD边上的点E处，折痕为MN．若CE的长为7cm，则MN的长为（ ）

A 10 B. 13 C. 15 D. 无法求出
二、填 空 题（每小题3分，共15分）
11. 式子 中x的取值范围是_______________．
12. 若x=，则代数式x2+2x-1值为____________．
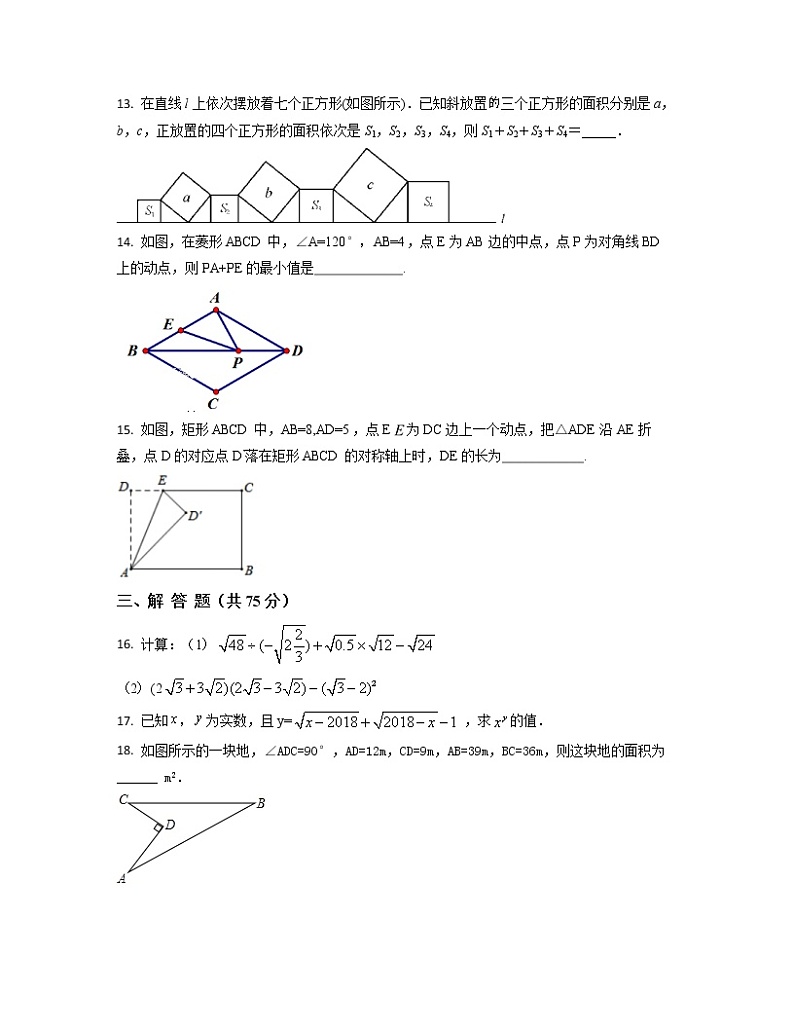
13. 在直线l上依次摆放着七个正方形(如图所示)．已知斜放置三个正方形的面积分别是a，b，c，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1＋S2＋S3＋S4＝_____．

14. 如图，在菱形ABCD中，∠A=120°，AB=4，点E为AB边的中点，点P为对角线BD上的动点，则PA+PE的最小值是_____________.

15. 如图，矩形ABCD中，AB=8,AD=5，点E为DC边上一个动点，把△ADE沿AE折叠，点D的对应点D’落在矩形ABCD的对称轴上时，DE的长为____________.

三、解 答 题（共75分）
16. 计算：（1）
（2）(2
17. 已知，为实数，且y= ，求的值．
18. 如图所示的一块地，∠ADC=90°，AD=12m，CD=9m，AB=39m，BC=36m，则这块地的面积为______ m2．


19. 如图，在△ABC中，AD平分，BD⊥AD，点E是BC边的中点，若AB=7,AC=12，求DE的长.

20. 如图，在矩形中，对角线和相交于点，，平分线交于点，连接，求的度数.


21. “为了，请勿超速”．如图，一条公路建成通车，在某直线路段MN限速60千米/小时，为了检测车辆是否超速，在公路MN旁设立了观测点C，从观测点C测得一小车从点A到达点B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200米，此车超速了吗．请说明理由．（参考数据：≈1.41，≈1.73）

22. 如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．
（1）求证：四边形CEDF是平行四边形；
（2）①当AE= cm时，四边形CEDF是矩形；
②当AE= cm时，四边形CEDF是菱形；（直接写出答案，没有需要说明理由）

2022-2023学年湖南省长沙市八年级下册数学期中专项提升模拟
（A卷）
一、选一选（每小题3分，共30分）
1. 下列二次根式中，最简二次根式的是（　　）
A. B. C. D.
【正确答案】C

【分析】判定一个二次根式是没有是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就没有是．
【详解】A、=，被开方数含分母，没有是最简二次根式；故A选项错误；
B、=，被开方数为小数，没有是最简二次根式；故B选项错误；
C、，是最简二次根式；故C选项正确；
D．=，被开方数，含能开得尽方的因数或因式，故D选项错误；
故选C．
考点：最简二次根式．
2. 下列以线段a、b、c的长为边的三角形中，没有能构成直角三角形的是（ ）
A. B.
C. D.
【正确答案】D

【分析】根据直角三角形的判定，符合a2+b2＝c2即可；反之没有符合的没有能构成直角三角形．
【详解】解：A、因为92+402＝412，故能构成直角三角形；
B、因为52+52=，故能构成直角三角形；
C、因为，故能构成直角三角形；
D、因为112+122≠152，故没有能构成直角三角形；
故选：D．
本题考查的是勾股定理的逆定理，当三角形中三边满足关系时，则三角形为直角三角形．
3. 如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于AB的长为半径画弧，两弧相交于C、D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（ ）

A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形
【正确答案】B

【详解】解：∵分别以A和B为圆心，大于AB的长为半径画弧，两弧相交于C、D，
∴AC=AD=BD=BC，
∴四边形ADBC一定是菱形，
故选：B．

4. 下列各式计算正确的是（　　）
A. B. C. D.
【正确答案】D

【详解】分析：A、根据算术平方根的计算法则计算即可作出判断；
B.根据二次根式的性质进行化简即可得出判断；
C. 根据二次根式的乘法法则计算即可求解；
D、根据二次根式的除法法则计算即可求解．
详解：A、与没有是同类二次根式，没有能合并，故该选项错误；
B、，故选项错误；
C.，故该选项错误；
D.，正确.
故选D.
点睛：二次根式的运算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．
5. 直角三角形两个直角边长分别是3、4，则这个直角三角形的第三边是（ ）
A. 5 B. C. 5或 D. 无法确定
【正确答案】A

【分析】3、4均为直角边,可根据勾股定理求第三边的长．
【详解】解：∵3、4的边都是直角边：
∴第三边的长为：＝5；
故选A．
此题主要考查的是勾股定理，解题的关键是熟知勾股定理的运用.
6. 如图，在周长为20cm的平行四边形ABCD中，AB≠AD，AC和BD相交于点O，OE⊥BD交AD于E，则ΔABE的周长为（ ）

A. 4cm B. 6cm C. 8cm D. 10cm
【正确答案】D

【分析】利用平行四边形、等腰三角形的性质，将△ABE的周长转化为平行四边形的边长之间的和差关系．
【详解】∵四边形ABCD是平行四边形，
∴AC、BD互相平分，
∴O是BD的中点．
又∵OE⊥BD，
∴OE为线段BD的垂直平分线，
∴BE=DE．
又∵△ABE的周长=AB+AE+BE，
∴△ABE的周长=AB+AE+DE=AB+AD．
又∵□ABCD 周长为20cm，
∴AB+AD=10cm
∴△ABE的周长=10cm．
故选D.
本题考查了平行四边形的性质和垂直平分线的性质．解题关键是掌握平行四边形的对角线互相平分．
7. 当1＜a＜2时，代数式＋|1－a|的值是( )
A. －1 B. 1 C. 2a－3 D. 3－2a
【正确答案】B

【详解】解：∵1＜a＜2，
∴=|a-2|=-（a-2），|1-a|=a-1，
∴+|1-a|
=-（a-2）+（a-1）
=2-1
=1．
故选B．
8. 将一根24cm的筷子，置于底面直径为15cm，高8cm的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度hcm，则h的取值范围是（　　）

A. h≤17cm B. h≥8cm
C. 15cm≤h≤16cm D. 7cm≤h≤16cm
【正确答案】D

【分析】如图，当筷子的底端在A点时，筷子露在杯子外面的长度最短；当筷子的底端在D点时，筷子露在杯子外面的长度最长．然后分别利用已知条件根据勾股定理即可求出h的取值范围．
【详解】解：如图，当筷子的底端在D点时，筷子露在杯子外面的长度最长，
∴h＝24﹣8＝16cm；
当筷子的底端在A点时，筷子露在杯子外面的长度最短，
在Rt△ABD中，AD＝15，BD＝8，
∴AB＝＝17，
∴此时h＝24﹣17＝7cm，
所以h的取值范围是7cm≤h≤16cm．
故选：D．

本题考查了勾股定理的应用，解题的关键是注意此题要求的是筷子露在杯外的取值范围，主要是根据勾股定理求出筷子在杯内的长度．
9. 如图，点P是矩形ABCD的边AD上的一动点，矩形的两条边AB、BC的长分别是6和8，则点P到矩形的两条对角线AC和BD的距离之和是（ ）

A. 4.8 B. 5 C. 6 D. 7.2
【正确答案】A

【详解】解：连接OP，
∵矩形的两条边AB、BC的长分别为6和8，
∴S矩形ABCD=AB•BC=48，OA=OC，OB=OD，AC=BD=10，
∴OA=OD=5，
∴S△ACD=S矩形ABCD=24，
∴S△AOD=S△ACD=12，
∵S△AOD=S△AOP+S△DOP=OA•PE+OD•PF
=×5×PE+×5×PF
=（PE+PF）
=12，
解得：PE+PF=4.8．
故选A．

本题考查矩形的性质；和差倍分；定值问题．
10. 如图，将边长为12cm的正方形ABCD折叠，使得点A落在CD边上的点E处，折痕为MN．若CE的长为7cm，则MN的长为（ ）

A 10 B. 13 C. 15 D. 无法求出
【正确答案】B

【详解】试题分析：作NF⊥AD，垂足为F，连接AE，NE，∵将正方形纸片ABCD折叠，使得点A落在边CD上的E点，折痕为MN，∴∠D=∠AHM=90°，∠DAE=∠DAE．∴△AHM∽△ADE．
∴∠AMN=∠AED．
在Rt△NFM和Rt△ADE中，
，
∴△NFM≌△ADE（AAS），
∴FM=DE=CD﹣CE=5cm，
又∵在Rt△MNF中，FN=AB=12cm，
∴根据勾股定理得：MN==13．
故选B．

考点： 翻折变换（折叠问题）．
二、填 空 题（每小题3分，共15分）
11. 式子 中x的取值范围是_______________．
【正确答案】x≥-1且x≠3

【详解】分析：根据二次根式和分式有意义的条件：被开方数大于等于0，分母没有等于0，就可以求解．
详解：根据题意，得
，
解得x≥-1，且x≠3．
故答案为x≥-1，且x≠3．
点睛：本题考查的知识点为：分式有意义，分母没有为0；二次根式的被开方数是非负数．
本题应注意在求得取值范围后，应排除没有在取值范围内的值．
12. 若x=，则代数式x2+2x-1的值为____________．
【正确答案】1

【详解】分析：先将x2+2x-1变形为（x+1）2-2，再把x=代入求值即可.
详解：∵x=
∴x2+2x-1=（x+1）2-2=3-2=1.
故答案为1.
点睛：做此类题的时候，应先得到只含字母的代数式的值为多少，把要求的式子整理成包含那个代数式的形式．
13. 在直线l上依次摆放着七个正方形(如图所示)．已知斜放置的三个正方形的面积分别是a，b，c，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1＋S2＋S3＋S4＝_____．

【正确答案】a+c

【分析】运用勾股定理可知，每两个相邻的正方形面积和都等于中间斜放的正方形面积，据此即可解答．
【详解】解：

∵∠ACB+∠DCE=90°，∠BAC+∠ACB=90°，
∴∠DCE=∠BAC，
∵AC=CE，∠ABC=∠CDE
∴△ABC≌△CDE，
∴BC=DE，
在直角△ABC中，AB2+BC2=AC2，
即AB2+DE2=AC2，
∵S3=AB2，S4=DE2
∴S3+S4=c
同理S1+S2=a
故可得S1+S2+S3+S4=a+c，
故答案是： a+c．
本题考查正方形面积的计算，正方形各边相等的性质，全等三角形的判定．解题关键是本题中根据△ABC≌△CDE证明S3+S4=c
14. 如图，在菱形ABCD中，∠A=120°，AB=4，点E为AB边的中点，点P为对角线BD上的动点，则PA+PE的最小值是_____________.

【正确答案】2

【详解】分析：根据轴对称的性质，首先准确找到点P的位置．根据菱形的性质，知：点A和C关于BD对称．则连接CE交BD于点P，P即为所求作的点．PE+PA的最小值即为CE的长．
详解：∵∠A=120°，
∴∠ABC=60°，AB=AC
∴△ABC是等边三角形
∴CE⊥AB
∴CE=

故答案为.
点睛：此题的难点在于能够正确找到点P的位置．注意综合运用等边三角形的判定、等腰三角形的三线合一、勾股定理、菱形的四边相等进行求解．
15. 如图，矩形ABCD中，AB=8,AD=5，点E为DC边上一个动点，把△ADE沿AE折叠，点D的对应点D’落在矩形ABCD的对称轴上时，DE的长为____________.

【正确答案】或

【详解】分析：过点D′作MN⊥AB于点N，MN交CD于点M，由矩形有两条对称轴可知要分两种情况考虑，根据对称轴的性质以及折叠的特性可找出各边的关系，在直角△EMD′与△AND′中，利用勾股定理可得出关于DM长度的一元二次方程，解方程即可得出结论．
详解：过点D′作MN⊥AB于点N，MN交CD于点M，如图1、所示．

设DE=a，则D′E=a．
∵矩形ABCD有两条对称轴，
∴分两种情况考虑：
①当DM=CM时，
AN=DM=CD=AB=4，AD=AD′=5，
由勾股定理可知：
ND′=，
∴MD′=MN-ND′=AD-ND′=2，EM=DM-DE=4-a，
∵ED′2=EM2+MD′2，即a2=（4-a）2+4，
解得：a=；
②当MD′=ND′时，
MD′=ND′=MN=AD=，
由勾股定理可知：
AN=，
∴EM=DM-DE=AN-DE=-a，
∵ED′2=EM2+MD′2，即a2＝(−a)2+()2，
解得：a=．
综上知：DE=或．
故答案为或．．
点睛：本题考查了翻转变换、轴对称的性质、矩形的性质以及勾股定理，解题的关键是找出关于DM长度的一元二次方程．本题属于中档题，难度没有大，但在做题过程中容易丢失一种情况，解决该题型题目时，勾股定理列出方程是关键．
三、解 答 题（共75分）
16. 计算：（1）
（2）(2
【正确答案】(1);(2)

【详解】分析：（1）先把各二次根式进行化简，再进行乘法运算，合并同类二次根式即可得解；
（2）分别运用平方差公式和完全平方公式进行计算，进行加减运算即可.
详解（1）原式=.
（2）原式=.
点睛：本题考查的是二次根式的混合运算，掌握二次根式的性质、二次根式的混合运算法则是解题的关键．
17. 已知，为实数，且y= ，求的值．
【正确答案】

【详解】分析：利用负数没有平方根求出x的值，进而确定出y的值，即可求出原式的值．
详解：满足二次根式有意义，则
，
解得：x=2018，
∴y=0-0-1=-1，
∴=2018-1=．
点睛：此题考查了立方根，平方根，以及二次根式有意义的条件，熟练掌握各自的定义是解本题的关键．
18. 如图所示的一块地，∠ADC=90°，AD=12m，CD=9m，AB=39m，BC=36m，则这块地的面积为______ m2．


【正确答案】216

【分析】连接AC，根据直角△ACD可以求得斜边AC的长度，根据AC，BC，AB可以判定△ABC为直角三角形，要求这块地的面积，求△ABC与△ACD的面积之差即可．
【详解】连接AC，

在直角△ACD中，CD=9m，AD=12m，
∴AD²+CD²=AC²，得AC=15m，
在△ABC中，AB=39m，BC=36m，AC=15m，
∴AC²+CB²=AB²，
∴△ABC为直角三角形，
S==AC⋅BC−CD⋅AD=×15×36−×9×12=270−54=216m²，
答：这块地的面积为216m².
故填:216.
本题考查了勾股定理在实际生活中的运用，考查了直角三角形面积的计算，本题中正确的判定△ABC是直角三角形是解题的关键．
19. 如图，在△ABC中，AD平分，BD⊥AD，点E是BC边的中点，若AB=7,AC=12，求DE的长.

【正确答案】25

【详解】分析：延长BD交AC于点F，可证明△ABD≌△AFD，从而得出BD=DF，利用三角形的中位线定理，从而得出DE的长．
详解：延长BD交AC于点F，

平分，，
，.
为公共边，
∴△ADB≌△ADF，

，
.
点是边的中点，
.…
点睛：本题考查了三角形的中位线定理，以及等腰三角形的判定和性质．
20. 如图，在矩形中，对角线和相交于点，，的平分线交于点，连接，求的度数.


【正确答案】

【详解】分析：根据矩形的性质得出∠DCB=90°，AC=BD，AC=2CO，BD=2OD，求出OC=OD，得出△COD是等边三角形，求出∠ACB=30°，求出OC=CE，即可求出答案．
详解：四边形为矩形，

，
和均为等边三角形，即.
平分，
，
，

，，
，

点睛：本题考查了矩形的性质，等边三角形的性质和判定，角平分线定义的应用，解此题的关键是求出OC=CE和求出∠ACB的度数，综合性比较强，有一定的难度．
21. “为了，请勿超速”．如图，一条公路建成通车，在某直线路段MN限速60千米/小时，为了检测车辆是否超速，在公路MN旁设立了观测点C，从观测点C测得一小车从点A到达点B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200米，此车超速了吗．请说明理由．（参考数据：≈1.41，≈1.73）

【正确答案】此车没有超速，理由见解析．

【分析】根据题意锐角三角函数关系得出BH，CH，AB的长进而求出汽车的速度，进而得出答案．
【详解】解：此车没有超速．
理由：过C作CH⊥MN，
∵∠CBN=60°，BC=200米，
∴CH=BCsin60°=200×=100（米），
BH=BCcos60°=100（米），
∵∠CAN=45°，
∴AH=CH=100米，
∴AB=100﹣100≈73（m），
∵60千米/小时=m/s，
∴=14.6（m/s）＜≈16.7（m/s），
∴此车没有超速．

本题考查勾股定理以及锐角三角函数关系的应用．

22. 如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连接CE，DF．
（1）求证：四边形CEDF是平行四边形；
（2）①当AE= cm时，四边形CEDF是矩形；
②当AE= cm时，四边形CEDF是菱形；（直接写出答案，没有需要说明理由）

【正确答案】（1）证明见解析；（2）① 当AE＝3．5cm时，四边形CEDF是矩形．② 当AE＝2cm时，四边形CEDF是菱形．

【详解】解：（1）∵ 四边形ABCD是平行四边形，
∴ CF∥ED，
∴ ∠FCG＝∠EDG，
∵ G是CD的中点，
∴ CG＝DG，
在△FCG和△EDG中，
，
∴ △FCG ≌△EDG（ASA），
∴ FG＝EG，
∵ CG＝DG，
∴ 四边形CEDF是平行四边形；
(2)①当AE=3.5时，平行四边形CEDF是矩形，
理由是：过A作AM⊥BC于M，
∵∠B=60°，AB=3，
∴BM=1.5，
∵四边形ABCD是平行四边形，
∴∠CDA=∠B=60°，DC=AB=3，BC=AD=5，
∵AE=3.5，
∴DE=1.5=BM，
在△MBA和△EDC中，

∴△MBA≌△EDC(SAS)，
∴∠CED=∠AMB=90°，
∵四边形CEDF是平行四边形，
∴四边形CEDF是矩形，
故答案为3.5；
②当AE=2时，四边形CEDF是菱形，
理由是：
∵AD=5，AE=2，

∴DE=3，
∵CD=3，∠CDE=60°，
∴△CDE等边三角形，
∴CE=DE，
∵四边形CEDF是平行四边形，
∴四边形CEDF是菱形，
故答案为2.
本题考查平行四边形的性质、全等三角形的判定与性质、矩形的判定以及菱形的判定，综合形较强．








2022-2023学年湖南省长沙市八年级下册数学期中专项提升模拟
（B卷）

一．选一选(本大题共12个小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的)
1. 下列方程是一元二次方程是（ ）
A. B. C. D.
2. 小明骑车去学校，骑了一会后车子出了故障，修了一会，然后继续骑车去学校.如果用横坐标表示时间 t，纵坐标表示路程 s，下列各图能较好地反映 s 与 t 之间函数关系的是（ ）
A. B. C. D.
3. 函数y=(3m+2)x+m-1（m为常数）的图像原点，则m的值为（ ）
A. 0 B. 1 C. D. -2
4. 一元二次方程(x-1)2=9的解为（ ）
A 4 B. -2 C. 4或-2 D. 3或-3
5. 一元二次方程配方后可变形为（ ）
A. B. C. D.
6. 某演讲比赛中，评委将从演讲内容、演讲能力、演讲三个方面为选手打分，然后再按演讲内容占50%、演讲能力占40%、演讲占10%的比例计算选手的综合成绩．某选手的演讲内容、演讲能力、演讲成绩依次为85、90、95，则该选手的综合成绩为（ ）
A. 92 B. 88 C. 90 D. 95
7. 数据5，2，3，5，5，1，3的众数和中位数分别是（　　）
A. 5,4 B. 3,5 C. 5,5 D. 5,3
8. 为了比较甲乙两种水稻秧苗是否出苗更整齐，每种秧苗各取10株分别量出每株长度，发现两组秧苗的平均长度一样，甲、乙方差分别是3.9、15.8，则下列说确的是（ ）
A. 甲秧苗出苗更整齐 B. 乙秧苗出苗更整齐
C. 甲、乙出苗一样整齐 D. 无法确定
9. 已知函数y=mx+n﹣2的图象如图所示，则m、n的取值范围是（　　）

A. m＞0，n＜2 B. m＞0，n＞2 C. m＜0，n＜2 D. m＜0，n＞2
10. 某商品原价289元，经连续两次降价后售价为256元，设平均每降价的百分率为x，则下面所列方程正确的是（　　）
A. 289（1﹣x）2=256 B. 256（1﹣x）2=289
C. 289（1﹣2x）2=256 D. 256（1﹣2x）2=289
11. 如图，函数的图象与坐标轴的交点坐标分别为A（0,2），B（-3，0），下列说法：（1）随 的增大而减小；（2）；（3）关于的方程的解为；（4）关于的没有等式的解集.其中说确的有（ ）个

A. 1 B. 2 C. 3 D. 0
12. 如图所示，函数和的图像相交于，两点，当时，的取值范围是（ ）

A. B. C. 或 D.
二．填 空 题(本大题共6个小题，每小题3分，把答案填在答卷的横线上)
13. 一元二次方程x2＝2x的解为________．
14. 函数中，自变量的取值范围是 .
15. 函数的图像与两坐标轴围成的三角形的面积是_________.
16. 若关于x一元二次方程kx2+2(k+1)x+k－1=0有两个实数根，则k的取值范围是______．
17. 已知一元二次方程x2－4x－3＝0两根为m，n，则－mn＋=_______．
18. 已知函数的自变量满足时，函数值满足，则该函数解析式为_____________________.
三．解 答 题：(本大题共8小题，共66分，解答应写出文字说明、证明过程或演算步骤)
19. 解方程：（1） （2）
20. 已知关于的一元二次方程一个根为2，求的值及方程的另一根.
21. 如图，已知直线点A（-1，0）与点B（2，3），求直线对应函数的解析式．

22. 我国是世界上严重缺水的国家之一，某校为了组织“节约用水从我做起”，随机了本校120名同学家庭月人均用水量和节水措施情况，如图1、图2是根据结果做出的统计图的一部分．请根据信息解答下列问题：
(1)图1中淘米水浇花所在的扇形的圆心角度数为__________________；
(2)补全图2；
(3)求120名同学家庭月人均用水量的中位数和众数；
(4)如果全校学生家庭总人数为3000人，根据这120名同学家庭月人均用水量，估计全校学生家庭月用水总量是多少吨？

图1

图2
23. 如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD（围墙MN最长可利用25m），现在已备足可以砌50m长的墙的材料，试设计一种砌法，使矩形花园的面积为300m2．
24. 我市某林场计划购买甲、乙两种树苗共800株，甲种树苗每株24元，乙种树苗每株30元．相关资料表明：甲、乙两种树苗的成活率分别为85%、90%．
（1）若购买这两种树苗共用去21000元，则甲、乙两种树苗各购买多少株？
（2）若要使这批树苗的总成活率没有低于88%，则甲种树苗至多购买多少株？
（3）在（2）的条件下，应如何选购树苗，使购买树苗的费用？并求出费用．
25. 使得函数值为零的自变量的值称为函数的零点．例如，对于函数，令y=0，可得x=1，我们就说1是函数的零点．
已知函数(m为常数)．
（1）当=0时，求该函数的零点；
（2）证明：无论取何值，该函数总有两个零点；
（3）设函数的两个零点分别为和，且，此时函数图象与x轴的交点分
别为A、B(点A在点B左侧)，点M在直线上，当MA+MB最小时，求直线AM的函数解析式．
26. 如图，已知函数y=-x+7与正比例函数y=x的图像交于点A，且与x轴交于点B.
（1）求点A和点B坐标；
（2）过点A作AC⊥y轴于点C，过点B作直线l∥y轴．动点P从点O出发，以每秒1个单位长的速度，沿O—C—A的路线向点A运动；同时直线l从点B出发，以相同速度向左平移，在平移过程中，直线l交x轴于点R，交线段BA或线段AO于点Q．当点P到达点A时，点P和直线l都停止运动．在运动过程中，设动点P运动的时间为t秒.
①当t为何值时，以A、P、R为顶点的三角形的面积为8？
②是否存在以A、P、Q为顶点的三角形是等腰三角形？若存在，求t的值；若没有存在，请说明理由．











2022-2023学年湖南省长沙市八年级下册数学期中专项提升模拟
（B卷）

一．选一选(本大题共12个小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的)
1. 下列方程是一元二次方程的是（ ）
A. B. C. D.
【正确答案】A

【详解】分析：根据一元二次方程的定义逐项分析判断即可.
详解：A. ∵ ，
∴x2+x-2=0,
∴原方程是一元二次方程，故A正确；
B. 是一元方程，故B没有正确；
C. 是分式方程，故C没有正确；
D. 是二元二次方程，故D没有正确；
故选A.
点睛：本题考查了一元二次方程的定义，方程的两边都是整式，只含有一个未知数，并且整理后未知数的次数都是2，像这样的方程叫做一元二次方程，根据定义判断即可.
2. 小明骑车去学校，骑了一会后车子出了故障，修了一会，然后继续骑车去学校.如果用横坐标表示时间 t，纵坐标表示路程 s，下列各图能较好地反映 s 与 t 之间函数关系的是（ ）
A. B. C. D.
【正确答案】C

【详解】分析：利用函数图象定义和性质分析解答，把函数关系式中自变量的取值当作横坐标，相应的函数的取值当作纵坐标，在坐标系中描点、连线形成的图形就是函数的图象，在分析函数图象时要注意t、s轴所表示的实际意义.
详解：由于中途停车休息一段时间，时间增加，路程没有增加，排除A和B．
随着时间的增多，路程也随之增多，故排除D，应选C.
故选C．
点睛：本题主要考查了函数图象，是一道基础题，解题的关键是应首先看清横轴和纵轴所表示的量的意义，然后根据实际情况采用排除法求解即可．
3. 函数y=(3m+2)x+m-1（m为常数）的图像原点，则m的值为（ ）
A. 0 B. 1 C. D. -2
【正确答案】B

【详解】分析：y=mx+(m2-m)是函数则m≠0，，把（0，0）代入函数y=mx+(m2-m)得到：0=m2-m；根据m≠0、0=m2-m进而求得m的值即可.
详解：∵函数y=mx+(m2-m)的图像过原点（0，0），
∴0=m2-m且m≠0，
∴m=1.
故选B.
点睛：本题考查的是函数的图像和性质，一般地，形如y=kx+b（k≠0，k,b是常数），那么y叫做x的函数，熟练掌握函数图像上点的坐标与函数关系式之间的关系是解答本题的关键；
4. 一元二次方程(x-1)2=9的解为（ ）
A. 4 B. -2 C. 4或-2 D. 3或-3
【正确答案】C

【分析】根据方程的特点，用直接开平方法求解即可.
【详解】解：∵(x-1)2=9，
∴x-1=±3,
∴x= 4或x=-2.
故选：C.
本题考查了一元二次方程的解法，常用的方法有：直接开平方法，配方法，求根公式法，因式分解法，根据方程的特点灵活选用合适的方法是解答本题的关键.
5. 一元二次方程配方后可变形为（ ）
A. B. C. D.
【正确答案】C

【分析】先移项，再方程两边同加上16，即可得到答案．
【详解】，
，
，
，
故选C．
本题主要考查一元二次方程的配方，熟练掌握配方法是解题的关键．
6. 某演讲比赛中，评委将从演讲内容、演讲能力、演讲三个方面为选手打分，然后再按演讲内容占50%、演讲能力占40%、演讲占10%的比例计算选手的综合成绩．某选手的演讲内容、演讲能力、演讲成绩依次为85、90、95，则该选手的综合成绩为（ ）
A. 92 B. 88 C. 90 D. 95
【正确答案】B

【分析】根据加权平均数的计算公式列式计算可得．
【详解】该选手的综合成绩为85×50%+90×40%+95×10%=88分．
故选：B．
本题考查了加权平均数的求法，根据某方面的需要选拔时往往利用加权平均数更合适．
7. 数据5，2，3，5，5，1，3的众数和中位数分别是（　　）
A. 5,4 B. 3,5 C. 5,5 D. 5,3
【正确答案】D

【详解】分析：如果一组数据有奇数个，那么把这组数据从小到大排列后，排在中间位置的数是这组数据的中位数；如果一组数据有偶数个，那么把这组数据从小到大排列后，排在中间位置的两个数的平均数是这组数据的中位数. 一组数据中出现次数至多的数据叫做众数．
详解：∵5出现了3次，出现的次数至多，
∴众数是5；
∵从小到大排列后是：1,2,3,3,5,5,5，排在中间的数是3，
∴中位数是5.
故选D.
点睛：本题考查了中位数和众数的求法，解答本题的关键是熟练掌握中位数和众数的定义.
8. 为了比较甲乙两种水稻秧苗是否出苗更整齐，每种秧苗各取10株分别量出每株长度，发现两组秧苗的平均长度一样，甲、乙方差分别是3.9、15.8，则下列说确的是（ ）
A. 甲秧苗出苗更整齐 B. 乙秧苗出苗更整齐
C. 甲、乙出苗一样整齐 D. 无法确定
【正确答案】A

【详解】试题解析：∵甲、乙方差分别是3.9、15.8，
∴S2甲＜S2乙，
∴甲秧苗出苗更整齐；
故选A．
考点：方差．
9. 已知函数y=mx+n﹣2的图象如图所示，则m、n的取值范围是（　　）

A. m＞0，n＜2 B. m＞0，n＞2 C. m＜0，n＜2 D. m＜0，n＞2
【正确答案】D

【详解】试题分析：∵函数y=mx+n-2的图象过二、四象限，
∴m＜0，
∵函数图象与y轴交于正半轴，
∴n-2＞0，
∴n＞2．
故选D．
考点：函数图象与系数的关系．
10. 某商品原价289元，经连续两次降价后售价为256元，设平均每降价的百分率为x，则下面所列方程正确的是（　　）
A. 289（1﹣x）2=256 B. 256（1﹣x）2=289
C. 289（1﹣2x）2=256 D. 256（1﹣2x）2=289
【正确答案】A

【分析】增长率问题，一般用增长后的量=增长前的量×（1+增长率），本题可参照增长率问题进行计算，如果设平均每次降价的百分率为x，可以用x表示两次降价后的售价，然后根据已知条件列出方程．
【详解】根据题意可得两次降价后售价为289（1-x）2，
∴方程为289（1-x）2=256．
故选：A．
11. 如图，函数的图象与坐标轴的交点坐标分别为A（0,2），B（-3，0），下列说法：（1）随 的增大而减小；（2）；（3）关于的方程的解为；（4）关于的没有等式的解集.其中说确的有（ ）个

A. 1 B. 2 C. 3 D. 0
【正确答案】B

【详解】分析：根据函数性质,函数与一元方程的关系对个小题分析判断即可得解.
详解：①由图像知，y随x的增大而增大,故本小题错误;
②∵A（0,2），∴直线与y轴正半轴相交且b=2,故本小题正确;
③∵B（-3，0），关于x的方程的解为；故本小题错误;
④由图像知，的解集是,故本小题正确;
综上所述,说确的是②④.
故选B.
点睛：本题主要考查了函数的性质,函数与一元方程、一元没有等式的关系,利用数形是求解的关键.
12. 如图所示，函数和的图像相交于，两点，当时，的取值范围是（ ）

A. B. C. 或 D.
【正确答案】C

【分析】首先由已知得出y1＝x或y1＝−x又相交于（−1，1），（2，2）两点，根据y1＞y2图像的位置关系，即可求出x的取值范围．
【详解】解：∵当x≥0时，y1＝x；当x＜0时，y1＝−x， 两直线的交点为（2，2），（−1，1），
∴由图象可知：当y1＞y2时x的取值范围为：x＜−1或x＞2．
故选C．
此题考查的是两条直线相交问题，关键是掌握，当y1＞y2时x的取值范围等价于y1所对应的图像在y2所对应的图像上方部分图像上点的横坐标的范围．
二．填 空 题(本大题共6个小题，每小题3分，把答案填在答卷的横线上)
13. 一元二次方程x2＝2x的解为________．
【正确答案】x1＝0，x2＝2

【详解】移项得x2-2x=0，即x（x-2）=0，
解得x=0或x=2．
故
14. 函数中，自变量的取值范围是 .
【正确答案】．

【分析】求函数自变量的取值范围，就是求函数解析式有意义的条件，二次根式有意义的条件是：被开方数为非负数．
【详解】依题意，得x-3≥0，
解得：x≥3．
本题考查的知识点为：二次根式的被开方数是非负数．
15. 函数的图像与两坐标轴围成的三角形的面积是_________.
【正确答案】9

【详解】分析：首先求出直线y=2x-6与x轴、y轴的交点的坐标，然后根据三角形的面积公式得出结果．
详解：∵当x=0时，y=0-6=-6，
∴图像与y轴的交点是（0，-6）；
∵当y=0时，2x-6=0,
∴x=3,
∴图像与x轴的交点是（3,0）；
∴S△AOB=×3×6=9．
故答案为9．
点睛：本题考查了函数图像与坐标轴的交点问题，分别令x=0和y=0求出图像与坐标轴的交点是解答本题的关键.
16. 若关于x的一元二次方程kx2+2(k+1)x+k－1=0有两个实数根，则k的取值范围是______．
【正确答案】k≥，且k≠0

【分析】若一元二次方程有两个等实数根，则根的判别式Δ＝b2﹣4ac≥0，建立关于k的没有等式，求出k的取值范围．还要注意二次项系数没有为0．
【详解】解：∵关于x的一元二次方程kx2+2（k+1）x+k﹣1＝0有两个实数根，
∴Δ＝4（k+1）2﹣4k（k﹣1）＝12k+4≥0，且k≠0．
解得：k且k≠0，
∴故本题答案：k，且k≠0．
总结：（1）一元二次方程根的情况与判别式△的关系：①Δ＞0⇔方程有两个没有相等的实数根；②Δ＝0⇔方程有两个相等的实数根；③Δ＜0⇔方程没有实数根．（2）一元二次方程的二次项系数没有为0．
17. 已知一元二次方程x2－4x－3＝0的两根为m，n，则－mn＋=_______．
【正确答案】25

【详解】试题分析：由m与n为已知方程的解，利用根与系数的关系求出m+n=4，mn=﹣3，将所求式子利用完全平方公式变形后，即﹣mn+=﹣3mn=16+9=25．
故答案为25．
考点：根与系数关系．

18. 已知函数的自变量满足时，函数值满足，则该函数解析式为_____________________.
【正确答案】y=2x-5,y=-2x-1

【详解】分析：确定函数的解析式一般要运用待定系数法，这就需要知道函数图形上的两个点坐标，根据题意可知图象的两点坐标是（-1，-7）、（3,1）或（-1，1）、（3,-7）.
详解：根据题意，①当k>0时，y随x增大而增大，
∴当x=-1时，y=-7；x=3时，y=1,
∴ ，
∴解得： ，
∴函数解析式为：y=2x-5；
②当k0时，y随x的增大而增大，当k