2022-2023学年北京市三校联考八年级下册数学期中专项提升模拟（卷一卷二）含解析

这是一份2022-2023学年北京市三校联考八年级下册数学期中专项提升模拟（卷一卷二）含解析，共47页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。
2022-2023学年北京市三校联考八年级下册数学期中专项提升模拟（卷一）
一、选一选：(本大题共8小题，每小题3分，共24分)
1. 十二边形的内角和为（ ）
A 1080° B. 1360° C. 1620° D. 1800°
2. 在Rt△ABC中，∠ACB=90°，AC=CB，CD是斜边AB的中线，若AB=2，则点D到BC的距离为（ ）
A. 1 B. C. 2 D.
3. 若点A（m，n）在第二象限，那么点B（﹣m，|n|）在（　　）.
A 象限 B. 第二象限 C. 第三象限 D. 第四象限
4. 在△ABC中，∠C=90°，AD为角平分线，BC=32，BD∶DC=9∶7, 则点D到AB的距离为（ ）
A. 18cm B. 16cm C. 14cm D. 12cm
5. 已知点P (3k – 2，2k – 3 )在第四象限．那么k的取值范围是（ ）
A. B. k＜ C. k＞ D. 都没有对
6. 菱形具有而矩形没有具有的性质是（　　）
A. 对角线互相平分 B. 四条边都相等
C 对角相等 D. 邻角互补
7. 如图，矩形ABCD中，DE⊥AC于E，且∠ADE：∠EDC=3:2，则∠BDE的度数为（ ）．

A. 36° B. 18° C. 27° D. 9°
8. 如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（3，2），点D、E分别在AB、BC边上，BD=BE=1．沿直线DE将△BDE翻折，点B落在点B′处．则点B′的坐标为( ).

A. （1，2） B. （2，1） C. （2，2） D. （3，1）
二、填 空 题：(本大题共8小题，每小题3分，共24分)
9. 如果点M（a-1，a+1）在x轴上，则a的值为___________.
10. ΔABC中,∠C＝90°，AB＝10，∠A＝30°，则BC=______,AC=______.
11. 点（3，）关于轴的对称点的坐标是__________．
12. 平行四边形ABCD中，∠A=50°，AB=30cm，则∠B=_____，DC=_____cm．
13. 若矩形的对角线长为8cm，两条对角线的一个交角为60°，则该矩形的面积为__cm2
14. 已知Rt△ABC中，斜边AB=10cm，则斜边上的中线的长为______.
15. 如图，在中，，，，线段，，两点分别在和过点且垂直于的射线上运动，当__________时，和全等．

16. 如图，动点在平面直角坐标系中按图中箭头所示的方向运动，第1次从原点运动到(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)，．．．按这样的运动规律，2019次运动后，动点的坐标为___________．

三、解 答 题（本大题共72分）
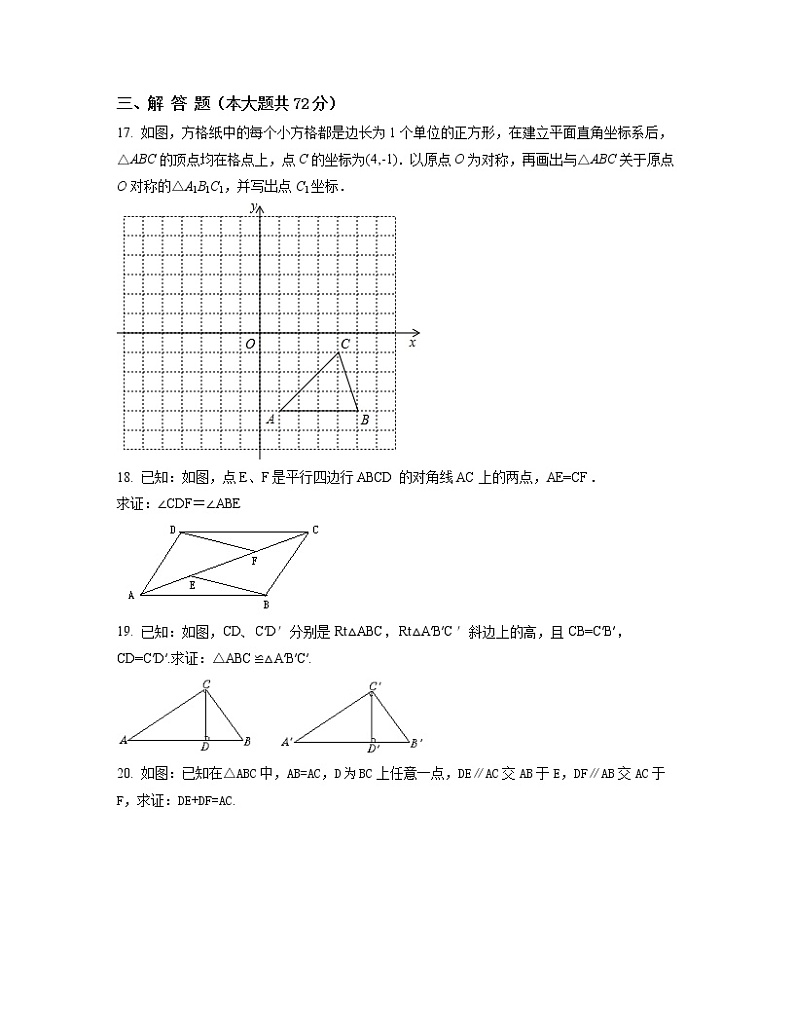
17. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为(4,-1)．以原点O为对称，再画出与△ABC关于原点O对称的△A1B1C1，并写出点C1坐标．

18. 已知：如图，点E、F是平行四边行ABCD的对角线AC上的两点，AE=CF．
求证：∠CDF＝∠ABE

19. 已知：如图，CD、C′D′分别是Rt△ABC，Rt△A′B′C′斜边上的高，且CB=C′B′，CD=C′D′.求证：△ABC≌△A′B′C′.

20. 如图：已知在△ABC中，AB=AC，DBC上任意一点，DE∥AC交AB于E，DF∥AB交AC于F，求证：DE+DF=AC.

21. 如图，直角三角形OAB中，∠AOB＝90°，∠A＝60°∠xOA＝30°，AB与y轴的交点坐标D为（0，4）．求A、B的坐标.

22. 如图，已知ΔABC在坐标平面内的顶点C（2，0），∠ACB＝90°，∠B＝30°，AB＝6，∠BCD＝45°．①求A、B的坐标；②求AB中点M的坐标.

23. 已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，猜想四边形ADCE的形状，并给予证明．

24. 如图，在梯形纸片ABCD中，AD//BC，AD>CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C处，折痕DE交BC于点E，连结C′E．
求证：四边形CDC′E是菱形．

25. 如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于点D，CE⊥DE于点E．

（1）若B、C在DE同侧（如图所示），且AD=CE．求证：AB⊥AC；
（2）若B、C在DE的两侧（如图所示），其他条件没有变，AB与AC仍垂直吗？若是请给出证明；若没有是，请说明理由．

26. 数学课上，老师留下了这样一道题“任画一个△ABC，以BC的中点O为对称，作△ABC的对称图形，问△ABC与它的对称图形拼成了一个什么形状的四边形？并说明理由.”
于是大家讨论开了，小亮说：“拼成的是平行四边形”； 小华说：“拼成的是矩形”；
小强说：“拼成的是菱形”； 小红说：“拼成的是正方形”；其他同学也说出了自己的看法……你赞同他们中的谁的观点？为什么？若都没有赞同，请说出你的观点（画出图形），并说明理由.













2022-2023学年北京市三校联考八年级下册数学期中专项提升模拟（卷一）
一、选一选：(本大题共8小题，每小题3分，共24分)
1. 十二边形的内角和为（ ）
A. 1080° B. 1360° C. 1620° D. 1800°
【正确答案】D

【详解】分析：根据多边形的内角和公式（n-2）•180°列式计算即可得解.
详解：：（12-2）•180°=1800°．
故选D．
点睛：本题考查了多边形内角与外角，熟记多边形内角和公式是解题的关键.
2. 在Rt△ABC中，∠ACB=90°，AC=CB，CD是斜边AB的中线，若AB=2，则点D到BC的距离为（ ）
A. 1 B. C. 2 D.
【正确答案】A

【详解】分析：根据等腰直角三角形的性质得出AC=CB=2，根据三角形的中线把三角形分成面积相等的两部分，利用面积计算即可.
详解：∵Rt△ABC中，∠ACB=90°，AC=CB，AB=2，
∴AC=CB=2，
∵CD是斜边AB的中线，
∴△DCB的面积=△ABC的面积=××2×2=1，
∴△DCB的面积=BC•点D到BC的距离=×2•点D到BC的距离=1，
∴点D到BC的距离=1，
故选A
点睛：此题考查了等腰直角三角形的性质，关键是根据三角形的中线把三角形分成面积相等的两部分分析．
3. 若点A（m，n）在第二象限，那么点B（﹣m，|n|）在（　　）.
A. 象限 B. 第二象限 C. 第三象限 D. 第四象限
【正确答案】A

【详解】解：因为点A在第二象限，
所以m0
所以-m>0，︱n︱>0，
因此点B在象限．
故选：A．
4. 在△ABC中，∠C=90°，AD为角平分线，BC=32，BD∶DC=9∶7, 则点D到AB的距离为（ ）
A. 18cm B. 16cm C. 14cm D. 12cm
【正确答案】C

【详解】试题解析：如图所示．

作DE⊥AB于E点．
∵BC=32，BD：DC=9：7，
∴CD=32×=14．
∵AD平分∠CAB，∠C=90°，DE⊥DE，
∴DE=DC=14．
即D点到AB的距离是14cm．
故选C．
考点：角平分线的性质．
5. 已知点P (3k – 2，2k – 3 )在第四象限．那么k的取值范围是（ ）
A. B. k＜ C. k＞ D. 都没有对
【正确答案】A

【详解】分析：点在第四象限条件是：横坐标是正数，纵坐标是负数.
详解：∵点P（3k-2，2k-3）在第四象限，
∴ ，解得 ＜k＜．
故选A
点睛：坐标平面被两条坐标轴分成了四个象限，每个象限内的点的坐标符号各有特点．该知识点是中考的常考点，常与没有等式、方程求一些字母的取值范围，比如本题中求k的取值范围.
6. 菱形具有而矩形没有具有的性质是（　　）
A. 对角线互相平分 B. 四条边都相等
C. 对角相等 D. 邻角互补
【正确答案】B

【详解】解：菱形的对角线互相垂直平分，四条边都相等，对角相等，邻角互补；
矩形的对角线互相平分且相等，对边相等，四个角都是90°.
菱形具有而矩形没有具有的性质是：四条边都相等，
故选B．
7. 如图，矩形ABCD中，DE⊥AC于E，且∠ADE：∠EDC=3:2，则∠BDE度数为（ ）．

A. 36° B. 18° C. 27° D. 9°
【正确答案】B

【详解】解：∵∠ADE：∠EDC=3：2
∴∠ADE=54°，∠EDC=36°，
又∵DE⊥AC，
∴∠DCE=90°-36°=54°，
根据矩形的性质可得∠DOC=180°-2×54°=72°，
∴∠BDE=180°-∠DOC-∠DEO=18°．
故选B．

8. 如图，矩形OABC的边OA、OC分别在x轴、y轴上，点B的坐标为（3，2），点D、E分别在AB、BC边上，BD=BE=1．沿直线DE将△BDE翻折，点B落在点B′处．则点B′的坐标为( ).

A. （1，2） B. （2，1） C. （2，2） D. （3，1）
【正确答案】B

【详解】解：∵四边形OABC是矩形，
∴∠B=90°，
∵BD=BE=1，
∴∠BED=∠BDE=45°，
∵沿直线DE将△BDE翻折，点B落在点B′处，
∴∠B′ED=∠BED=45°，∠B′DE=′BDE=45°，B′E=BE=1，B′D=BD=1，
∴∠BEB′=∠BDB′=90°，
∵点B的坐标为（3，2），
∴点B′的坐标为（2，1）．
故选：B
二、填 空 题：(本大题共8小题，每小题3分，共24分)
9. 如果点M（a-1，a+1）在x轴上，则a的值为___________.
【正确答案】-1

【分析】根据x轴上的点纵坐标等于0列出方程求解得到a的值.
【详解】∵点M（a-1，a+1）在x轴上，
∴a+1=0，
解得a=-1，
故答案为:-1.
本题考查了点的坐标，熟记x轴上的点的纵坐标等于0是解题的关键.
10. ΔABC中,∠C＝90°，AB＝10，∠A＝30°，则BC=______,AC=______.
【正确答案】 ①. 5 ②. 5

【详解】分析：由含30°角的直角三角形的性质求出BC，由勾股定理求出AC即可；
详解：）∵在Rt△ABC中，∠C=90°，AB=4，∠A=30°，
∴BC=AB=5，
∴AC=BC=5；
故答案为5，5.
点睛：本题考查了勾股定理、直角三角形的性质；熟练掌握勾股定理是解决问题的关键.
11. 点（3，）关于轴的对称点的坐标是__________．
【正确答案】（3,2）

【分析】利用关于x轴对称点的坐标特点：横坐标没有变，纵坐标互为相反数．即点P（x，y）关于x轴的对称点P'的坐标是（x，﹣y），进而求出即可．
【详解】点（3，﹣2）关于x轴的对称点坐标是（3，2）．
故答案为（3，2）．
本题考查了关于x轴对称点的性质，正确记忆横纵坐标的关系是解题的关键．
12. 平行四边形ABCD中，∠A=50°，AB=30cm，则∠B=_____，DC=_____cm．
【正确答案】 ①. 130° ②. 30

【详解】试题分析：根据平行四边形的性质：平行四边形的对边相等且平行，即可求得．
解：∵四边形ABCD是平行四边形，
∴AD∥BC，DC=AB=30cm，
∴∠A+∠B=180°，
∵∠A=50°，
∴∠B=130°．
故答案为130°，30．
13. 若矩形的对角线长为8cm，两条对角线的一个交角为60°，则该矩形的面积为__cm2
【正确答案】

【分析】根据等边三角形的判定，勾股定理和矩形的性质可求得答案.
【详解】∵四边形ABCD是矩形，
∴AC=BD，OA=OC，OD=OB，
∴OA=OB，
∵∠AOB=60°，
∴△AOB是等边三角形，
∴OA=OB=AB=AC=4，
∵矩形ABCD，
∴AB=CD=4，∠ABC=90°，
在△ABC中，由勾股定理得：BC=4
∴矩形的面积=4×4=16．
故．

此题主要考查了矩形对角线相等且互相平分的性质，等边三角形的判定，熟练掌握性质定理是解题的关键．
14. 已知Rt△ABC中，斜边AB=10cm，则斜边上的中线的长为______.
【正确答案】5

【详解】分析：根据直角三角形斜边上的中线的相关性质，即可推出CD的长度
详解：：∵Rt△ABC中，斜边AB的=10cm，CD为中线，
∴2CD=AB，
∴CD=5cm．
故答案为5.
点睛：本题主要考查直角三角形的相关性质，关键在于熟练运用直角三角形斜边上的中线的性质，认真的进行计算.
15. 如图，在中，，，，线段，，两点分别在和过点且垂直于的射线上运动，当__________时，和全等．

【正确答案】5或10

【分析】当AP＝5或10时，△ABC和△PQA全等，根据HL定理推出即可．
【详解】解：∵∠C＝90°，AO⊥AC，
∴∠C＝∠QAP＝90°，
①当AP＝5＝BC时，
在Rt△ACB和Rt△QAP中
∵，
∴Rt△ACB≌Rt△QAP（HL），
②当AP＝10＝AC时，
在Rt△ACB和Rt△PAQ中
，
∴Rt△ACB≌Rt△PAQ（HL），
故5或10．
本题考查了全等三角形的判定定理的应用，注意：判定两直角三角形全等的方法有ASA，AAS，SAS，SSS，HL．
16. 如图，动点在平面直角坐标系中按图中箭头所示的方向运动，第1次从原点运动到(1，1)，第2次接着运动到点(2，0)，第3次接着运动到点(3，2)，．．．按这样的运动规律，2019次运动后，动点的坐标为___________．

【正确答案】(2019，2)

【分析】先找出点的横坐标的变化规律即可求出2019次运动后，动点的横坐标，然后找出点的纵坐标的变化规律即可求出结论．
【详解】解：由坐标可知：动点的横坐标变化为：1、2、3、4……
∴2019次运动后，动点的横坐标为2019
动点的纵坐标变化为：1、0、2、0、1、0、2、0……每4个数字一循环
2019÷4=504……3
∴2019次运动后，动点的纵坐标为2
∴2019次运动后，动点的坐标为(2019，2)
故(2019，2)．
此题考查的是探索坐标的规律题，找出横、纵坐标的变化规律是解决此题的关键．
三、解 答 题（本大题共72分）
17. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为(4,-1)．以原点O为对称，再画出与△ABC关于原点O对称的△A1B1C1，并写出点C1坐标．

【正确答案】作图见解析，C1（-4，1）

【详解】利用关于原点对称点的坐标性质得出对应点位置进而得出答案．
△A1B1C1如图所示，


C1（-4，1）
此题主要考查网格作图，熟练掌握对称的定义是解题关键．
18. 已知：如图，点E、F是平行四边行ABCD的对角线AC上的两点，AE=CF．
求证：∠CDF＝∠ABE

【正确答案】见解析

【分析】根据平行四边形的性质证得CD=AB，∠DCF=∠EAB，又AE=CF，所以△CDF≌ACBE得证．
【详解】∵四边形ABCD是平行四边形，
∴CD=AB，CD//AB，
∴∠DCF=∠EAB，
，
∴△CDF≌ACBE（SAS）
∴∠CDF＝∠ABE．
本题考查了平行四边形的性质，全等三角形的判定与性质，熟练掌握平行四边形的性质是解答本题的关键．
19. 已知：如图，CD、C′D′分别是Rt△ABC，Rt△A′B′C′斜边上的高，且CB=C′B′，CD=C′D′.求证：△ABC≌△A′B′C′.

【正确答案】见解析

【详解】分析：欲证△ABC≌△A′B′C′，根据已知条件，已经有∠ACB=∠A′C′B′=90°，CB=C′B′，即已知一边一角，由三角形全等的判定定理可知，还需有一对角相等或者边AC=A′C′．而根据已知条件CB=C′B′，CD=C′D′，易证Rt△CDB≌Rt△C′D′B′，得出∠B=∠B′，从而根据ASA证明出△ABC≌△A′B′C′.
详解：
证明：∵CD⊥AB，C'D'⊥A'B' (已知)
∴∠CDB=∠C'D'B'=90°．(垂直的意义)
在Rt△CDB和Rt△C'D'B'中，
CB=C'B'，CD=C'D'，(已知)
∴Rt△CDB≌Rt△C'D'B'（HL），
∴∠B=∠B'，(全等三角形的对应角相等)
∵△ABC，△A'B'C'都是直角三角形 (已知)
∴∠ACB=∠A'C'B'=90°(直角三角形的意义）
在△ABC和△A'B'C'中，
∠B=∠B'
CD=C'D'
∠ACB=∠A'B'C'
∴△ABC≌△A'B'C'（ASA）
点睛：本题考查了全等三角形的判定．三角形全等的判定是中考的，一般以考查三角形全等的方法为主，要判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
20. 如图：已知在△ABC中，AB=AC，DBC上任意一点，DE∥AC交AB于E，DF∥AB交AC于F，求证：DE+DF=AC.

【正确答案】见解析

【详解】分析：由题意可得四边形AEDF是平行四边形，得DE=AF再由等腰三角形的性质及平行线可得DF=CF，进而可求出其结论.
详解：
证明：∵DE∥AC，DF∥AB，
∴四边形AEDF是平行四边形，
∴DE=AF，
又AB=AC，
∴∠B=∠C，
∵DF∥AB，
∴∠CDF=∠B，
∴∠CDF=∠C，
∴DF=CF，
∴AC=AF+FC=DE+DF．
点睛：本题主要考查平行四边形的判定及性质以及等腰三角形的性质问题，能够熟练求解.
21. 如图，直角三角形OAB中，∠AOB＝90°，∠A＝60°∠xOA＝30°，AB与y轴的交点坐标D为（0，4）．求A、B的坐标.

【正确答案】点A的坐标为（2，2）；点B的坐标为：（-2，6）．

【详解】分析：首先过点A作AC⊥x轴于点C，由直角三角形OAB中，∠AOB=90°，∠A=60°，∠BOD=30°，易得△AOD是等边三角形，即可求得OA的长，然后由含30°角的直角三角形的性质，求得AC的长，由勾股定理即可求得OC的长，则可求得答案．
详解：
过点A作AC⊥x轴于点C，

∵直角三角形OAB中，∠AOB=90°，∠A=60°，∠BOD=30°，
∴∠AOD=∠AOB-∠BOD=60°，
∴∠AOD=∠A，
∴OA=OD，
∴△AOD是等边三角形，
∵点D的坐标为（0，4），
∴OA=OD=4，
∵∠AOC=90°-∠AOD=30°，
∴AC=OA=2，
∴OC=，
∴点A的坐标为：（2，2）．
同理可得，点B的坐标为：（-2，6）．
点睛：此题考查了等边三角形的判定与性质，含30°角的直角三角形的性质以及勾股定理．此题难度适中，注意掌握辅助线的作法，注意掌握数形思想的应用.
22. 如图，已知ΔABC在坐标平面内的顶点C（2，0），∠ACB＝90°，∠B＝30°，AB＝6，∠BCD＝45°．①求A、B的坐标；②求AB中点M的坐标.

【正确答案】①A点坐标为（-1，3），B点坐标（2+3，3）；②AB中点M点坐标为

【详解】分析：①过A作AE⊥x轴于点E，过B作BD⊥x轴于点D，先解直角△ABC，得到AC=AB=3，BC=AC=3，再由△BCD是等腰直角三角形得出CD=BD=BC=3，由△ACE是等腰直角三角形得出AE=CE=AC=3, 再根据C的坐标为（2，0），即可求出A、B的坐标；
②由A、B两点的坐标，根据中点坐标公式即可求出AB中点M的坐标.
详解：
①过A作AE⊥x轴于点E，过B作BD⊥x轴于点D．
在△ABC中，∵∠ACB=90°，∠B=30°，AB=6，
∴AC=AB=3，BC=AC=3．
在△BCD中，∵∠BDC=90°，∠BCD=45°，
∴∠BCD=45°，
∴CD=BD=BC=3．
在△ACE中，∵∠AEC=90°，∠ACE=45°，
∴AE=CE=AC=3．
∵C（2，0），
∴OC=2，
∴OE=CE-OC=1，
∴A点坐标为（-1，3）．
∵OD=OC+CD=2+3,
∴B点坐标（2+3，3）
②A点坐标为（-1，3），B点坐标（2+3，3），
∴AB中点M点坐标为
点睛：本题考查了解直角三角形，坐标与图形性质，含30度角的直角三角形的性质，等腰直角三角形的判定与性质，线段中点坐标公式，综合性较强，难度适中.
23. 已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，猜想四边形ADCE的形状，并给予证明．

【正确答案】四边形ADCE是矩形．理由见解析．

【详解】试题分析：因为AD⊥BC，CE⊥AN，所以∠ADC=∠CEA=90°,然后根据互补和角平分线证明∠DAE=90°即可．
试题解析：四边形ADCE是矩形．
证明：因为AB=AC,AD⊥BC,所以∠BAD=∠CAD（三线合一）,
又因为AN平分∠CAM,∠BAC+∠CAM=180°,所以∠CAD+∠CAN=180°/2=90°,
又因为CE⊥AN,
所以AD∥CE,∠ADC=∠CEA=∠DAE=90°,则∠DCE=90°,
所以四边形ADCE是矩形．
考点：1．等腰三角形的性质；2．角的平分线；3．互补；4．矩形的判定．
24. 如图，在梯形纸片ABCD中，AD//BC，AD>CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C处，折痕DE交BC于点E，连结C′E．
求证：四边形CDC′E是菱形．

【正确答案】见解析

【详解】分析：依题意∠C′DE=∠CDE，CD=C′D，CE=C′E，又AD∥BC，∴∠C′DE=∠DEC，∴∠DEC=∠CDE，∴CD=CE，则四边相等，可得四边形CDC′E是菱形.
详解：
证明：∠ADE＝∠1,∠CED＝∠2,∠CDE＝∠3
∵AD‖BC
∴∠1＝∠2
又∵∠1＝∠3
∴∠2＝∠3
∴CE＝CD
又∵CD＝C'D
∴CE＝C'D
又∵CE‖C'D
∴四边形CEC'D是平行四边形
又∵CE＝CD
∴四边形CEC'D是菱形
点睛：本题主要考查四边形知识，考查学生的论证能力及思维逻辑能力.
25. 如图，在△ABC中，AB=AC，DE是过点A的直线，BD⊥DE于点D，CE⊥DE于点E．

（1）若B、C在DE的同侧（如图所示），且AD=CE．求证：AB⊥AC；
（2）若B、C在DE的两侧（如图所示），其他条件没有变，AB与AC仍垂直吗？若是请给出证明；若没有是，请说明理由．

【正确答案】（1）详见解析；（2）AB⊥AC，理由详见解析

【分析】（1）根据“HL”证明Rt△ABD≌Rt△CAE，得到∠DAB=∠ECA，∠DBA=∠EAC， 进而证明∠BAC=90°，问题得证；
（2）根据“HL”证明Rt△ABD≌Rt△CAE，得到∠DAB=∠ECA，∠DBA=∠EAC， 进而证明∠BAC=90°，问题得证．
【详解】（1）证明：∵BD⊥DE，CE⊥DE，
∴∠ADB=∠AEC=90°，
在Rt△ABD和Rt△CAE中，
∵，
∴Rt△ABD≌Rt△CAE，
∴∠DAB=∠ECA，∠DBA=∠EAC，
∵∠DAB+∠DBA=90°，∠EAC+∠ACE=90°，
∴∠BAD+∠CAE=90°，
∠BAC=180°-（∠BAD+∠CAE）=90°，
∴AB⊥AC．
（2）AB⊥AC．
理由如下：
证明：∵BD⊥DE，CE⊥DE，
∴∠ADB=∠AEC=90°，
在Rt△ABD和Rt△CAE中，
∵，
∴Rt△ABD≌Rt△CAE，
∴∠DAB=∠ECA，∠DBA=∠EAC，
∵∠CAE+∠ECA=90°，
∴∠CAE+∠BAD=90°，即∠BAC=90°，
∴AB⊥AC．
本题考查了全等三角形的判断与性质，当两个三角形为直角三角形时，除了常规的全等判定方法外，还有“HL”判定，要根据题意灵活选择，同时要注意在全等判定证明中注意对应．
26. 数学课上，老师留下了这样一道题“任画一个△ABC，以BC的中点O为对称，作△ABC的对称图形，问△ABC与它的对称图形拼成了一个什么形状的四边形？并说明理由.”
于是大家讨论开了，小亮说：“拼成的是平行四边形”； 小华说：“拼成的是矩形”；
小强说：“拼成的是菱形”； 小红说：“拼成的是正方形”；其他同学也说出了自己的看法……你赞同他们中的谁的观点？为什么？若都没有赞同，请说出你的观点（画出图形），并说明理由.
【正确答案】见解析

【详解】分析：考虑问题需要从多角度出发，三角形的种类有：①等腰非直角三角形；②等腰直角三角形；③非等腰三角形；④非等腰直角三角形；根据三角形的种类我们可以知道，此题有四种情况.
详解：没有赞同他们的观点，因为△ABC形状没有确定，所以应分情况讨论.
（1）若△ABC中，且时，如图1、图2.
△ABC与它的对称图形拼成了一个平行四边形.
理由：∵B与C、A与D关于O对称，
∴OA=OD，OB=OC，
∴四边形ABDC是平行四边形.

点睛：本题主要考查对作图-变换，作图-平移变换等知识点的理解和掌握，能根据题意正确画图是解此题的关键

























2022-2023学年北京市三校联考八年级下册数学期中专项提升模拟（卷二）
一、选一选（本题共10小题，每小题3分，共30分．）
1. 下列图案中既是轴对称图形，又是对称图形是(　　)
A. B. C. D.
2. 分式有意义，则x取值范围是（ ）
A. x ≠ 1 B. x＞1 C. x＜1 D. x ≠－1
3. 下列中，适合普查的是（　　）
A. 一批手机电池的使用寿命 B. 中国公民保护环境的意识
C. 你所在学校的男、女同学的人数 D. 端午节期间苏州市场上粽子的质量
4. 一个没有透明的袋子中装有2个红球、3个白球，每个球除颜色外都相同．从中任意摸出3个球，下列为必然的是(　　)
A. 至少有1个球红球 B. 至少有1个球是白球
C. 至少有2个球是红球 D. 至少有2个球是白球
5. 与分式－的值相等的是（ ）
A. － B. － C. D.
6. 矩形具有而平行四边形没有一定具有的性质是（ ）
A. 对角线互相平分 B. 两组对角相等
C. 对角线相等 D. 两组对边相等
7. 如图，在四边形中，分别是的中点，要使四边形是菱形，则四边形满足的一个条件是（ ）

A. 四边形是矩形 B. 四边形是菱形
C. D.
8. 如图，菱形ABCD中，对角线AC、BD相交于点O，H为AD边中点，菱形ABCD的周长为48，则OH的长等于（ ）

A. 12 B. 6 C. 4 D. 3
9. 如图，正方形纸片ABCD的边长为4 cm，点M、N分别在边AB、CD上．将该纸片沿MN折叠，使点D落在边BC上，落点为E，MN与DE相交于点Q．随着点M的移动，点Q移动路线长度的值是（ ）
\
A. 2 cm B. 4 cm C. cm D. 1 cm
10. 如图，是将菱形ABCD以点O为按顺时针方向分别旋转90°，180°，270°后形成的图形．若∠BAD＝60°，AB＝2，则图中阴影部分的面积为（　　）

A. 12﹣4 B. 5 C. 12﹣4 D. 6
二、填 空 题（本大题共8小题，每空2分，共16分）
11. 要使分式的值为0，则x的值为____________．
12. 一个袋中装有6个红球，4个黄球，1个白球，每个球除颜色外都相同，任意摸出一球，摸到____球的可能性
13. 从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如下：
种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
85
298
652
793
1604
4005
发芽频率
0.850
0.745
0.815
0.793
0.802
0.801

根据以上数据可以估计，该玉米种子发芽的概率约为___（到0.1）．
14. 在菱形ABCD中，对角线AC，BD的长分别是6和8，则菱形的周长是____________．
15. 如图，在Rt△ABC中，∠B＝90°，∠C＝30°，△ABC绕点A按顺时针方向旋转45°得△ADE，则∠BAE＝____________°．

16. 如图，在Rt△ABC中，∠C＝90°，将△ABC绕点C顺时针旋转90°得到△A′B′C，M、M′分别是AB、A′B′的中点，若AC＝4，BC＝2，则线段MM′的长为____．


17. 已知平面上四点，，，，直线将四边形分成面积相等的两部分，则的值为_______________．
18. 如图，在□ABCD中，BC=2AB，CE⊥AB于E，F为AD的中点，若∠AEF=54°，
则∠B=_________．

三、解答：（共74分）
19. 计算：
（1）
（2）
20. 先化简（1－ ）÷，再从﹣1，1，0，2四个数中，选一个恰当的数作为a的值代入求值．
21. 解方程：
（1）
（2）
22. 如图，在▱ABCD中，E、F为对角线BD上的两点，且AE⊥BD，CF⊥BD．
求证：BE=DF．

23. 已知的三个顶点的坐标分别为、、

（1）画出关于坐标原点成对称的；
（2）将绕坐标原点顺时针旋转，画出对应的；
（3）若以、、、为顶点四边形为平行四边形，则在第四象限中的点坐标为__________．
24. “摩拜单车”公司无锡市民对其产品的了解情况，随机抽取部分市民进行问卷，结果分“非常了解”、“比较了解”、“一般了解”、“没有了解”四种类型，分别记为A、B、C、D．根据结果绘制了如下尚没有完整的统计图．

（1）本次问卷共随机了　 　名市民，扇形统计图中m＝　 　．
（2）请根据数据信息补全条形统计图．
（3）扇形统计图中“D类型”所对应的圆心角的度数是　 　．
（4）从这次接受的市民中随机抽查一个，恰好是“没有了解”的概率是　 　．
25. 小军家距学校5千米，原来他骑自行车上学，学校为保障学生，新购进校车接送学生.若校车的速度是他骑车速度的2倍，则现在小军乘校车上学可以从家晚10分钟出发，结果与原来到校时间相同，试求小军骑车的速度.
26. 邻边没有相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；……依次类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，平行四边形中，若，则平行四边形为1阶准菱形．

（1）判断与推理：
① 邻边长分别为2和3的平行四边形是__________阶准菱形；
② 小明为了剪去一个菱形，进行如下操作：如图2，把平行四边形沿着折叠（点在上）使点落在边上的点，得到四边形，请证明四边形是菱形．
（2）操作、探究与计算：
① 已知平行四边形的邻边分别为1，裁剪线的示意图，并在图形下方写出的值；
② 已知平行四边形的邻边长分别为，满足，请写出平行四边形是几阶准菱形．
27. 如图，在直角坐标系中， B（0，8），D（10，0），函数y=x+的图象过C（16，n），与x轴交于A点．
（1）求证：四边形ABCD为平行四边形；
（2）将△AOB绕点O顺时针旋转，旋转得△A1OB1，问：能否使以点O、A1、D、B1为顶点四边形是平行四边形？若能，求点A1的坐标；若没有能，请说明理由；
















2022-2023学年北京市三校联考八年级下册数学期中专项提升模拟（卷二）
一、选一选（本题共10小题，每小题3分，共30分．）
1. 下列图案中既是轴对称图形，又是对称图形的是(　　)
A. B. C. D.
【正确答案】A

【详解】A.既是轴对称图形，又是对称图形；B.既没有是轴对称图形，又没有是对称图形；C.既没有是轴对称图形，又没有是对称图形；D是轴对称图形，没有是对称图形，故选A.
2. 分式有意义，则x的取值范围是（ ）
A. x ≠ 1 B. x＞1 C. x＜1 D. x ≠－1
【正确答案】A

【分析】根据分式有意义的条件：分母没有等于0，即可求解．
【详解】解：根据题意得：x﹣1≠0，
解得：x≠1．
故选：A．
本题主要考查了分式有意义的条件，正确理解条件是解题的关键．
3. 下列中，适合普查的是（　　）
A. 一批手机电池的使用寿命 B. 中国公民保护环境的意识
C. 你所在学校的男、女同学的人数 D. 端午节期间苏州市场上粽子的质量
【正确答案】C

【详解】一批手机电池的使用寿命适合抽样；
中国公民保护环境的意识适合抽样；
你所在学校的男、女同学的人数适合普查；
端午节期间苏州市场上粽子的质量适合抽样，
故选C.
4. 一个没有透明的袋子中装有2个红球、3个白球，每个球除颜色外都相同．从中任意摸出3个球，下列为必然的是(　　)
A. 至少有1个球是红球 B. 至少有1个球是白球
C. 至少有2个球是红球 D. 至少有2个球是白球
【正确答案】B

【详解】A. 至少有1个球是红球是随机，选项错误；
B. 至少有1个球是白球是必然，选项正确；
C. 至少有2个球是红球是随机，选项错误；
D. 至少有2个球是白球是随机，选项错误．
故选B.
5. 与分式－的值相等的是（ ）
A － B. － C. D.
【正确答案】D

【详解】因为－=，所以与分式－的值相等的是，故选D.
6. 矩形具有而平行四边形没有一定具有的性质是（ ）
A. 对角线互相平分 B. 两组对角相等
C. 对角线相等 D. 两组对边相等
【正确答案】C

【分析】

【详解】矩形的性质有：四个角都是直角，对角线相等且平分，对边平行且相等；
平行四边形的性质有：对角相等，对边相等且平行，对角线互相平分；
∴矩形具有但平行四边形没有一定具有的性质是对角线相等，
故选C．
7. 如图，在四边形中，分别是的中点，要使四边形是菱形，则四边形满足的一个条件是（ ）

A. 四边形是矩形 B. 四边形是菱形
C. D.
【正确答案】D

【详解】因为E，F，G，H是AB，BC，CD，DA的中点，所以EF=AD，EH∥BC且EH=BC，GF∥BC且GF=BC，所以四边形EFGH是平行四边形，当EF=EH，即AD=BC时，四边形EFGH是菱形，故选D.
8. 如图，菱形ABCD中，对角线AC、BD相交于点O，H为AD边中点，菱形ABCD的周长为48，则OH的长等于（ ）

A. 12 B. 6 C. 4 D. 3
【正确答案】B

【详解】因为菱形ABCD的周长为48，所以AD=48÷4=12，因为H为AD边的中点，∠AOD=90°，所以OH=AD=×12=6，故选B.
9. 如图，正方形纸片ABCD的边长为4 cm，点M、N分别在边AB、CD上．将该纸片沿MN折叠，使点D落在边BC上，落点为E，MN与DE相交于点Q．随着点M的移动，点Q移动路线长度的值是（ ）
\
A. 2 cm B. 4 cm C. cm D. 1 cm
【正确答案】A

【详解】如图，取AB，CD的中点K，G，连接KG，BD交于点O，由题意知，点Q运动的路线是线段OG，因为DO=OB，所以DG=GC，所以OG=BC=×4=2，所以点Q移动路线的值是2，故选A.

10. 如图，是将菱形ABCD以点O为按顺时针方向分别旋转90°，180°，270°后形成的图形．若∠BAD＝60°，AB＝2，则图中阴影部分的面积为（　　）

A. 12﹣4 B. 5 C. 12﹣4 D. 6
【正确答案】A

【详解】如图，连接AC，BD交于点E，连接DF，FM，MN，DN，
∵将菱形ABCD以点O为按顺时针方向分别旋转90°，180°，270°后形成的图形，∠BAD=60°，AB=2，
∴AC⊥BD，四边形DNMF是正方形，∠AOC=90°，BD=2，AE=EC=，
∴∠AOE=45°，ED=1，∴AE=EO=，DO=﹣1，
∴S正方形DNMF=2（﹣1）×2（﹣1）×=8﹣4，
S△ADF=×AD×AFsin30°=1，
∴则图中阴影部分的面积为：4S△ADF+S正方形DNMF=4+8﹣4=12﹣4．
故答案为12﹣4.

二、填 空 题（本大题共8小题，每空2分，共16分）
11. 要使分式值为0，则x的值为____________．
【正确答案】-2.

【分析】分式的值为零的条件是分子等于0且分母没有等于0，
【详解】因为分式的值为0，
所以x+2=0且x-1≠0，
则x=-2，
故答案为-2.
12. 一个袋中装有6个红球，4个黄球，1个白球，每个球除颜色外都相同，任意摸出一球，摸到____球的可能性
【正确答案】红

【详解】试题分析：根据袋子中的球的特点，可知红球至多，所以摸到红球的可能性.
故红.
13. 从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如下：
种子粒数
100
400
800
1000
2000
5000
发芽种子粒数
85
298
652
793
1604
4005
发芽频率
0.850
0.745
0.815
0.793
0.802
0.801

根据以上数据可以估计，该玉米种子发芽的概率约为___（到0.1）．
【正确答案】0.8

【分析】6批次种子粒数从100粒增加到5000粒时，种子发芽的频率趋近于0.801，所以估计种子发芽的概率为0.801，再到0.1，即可得出答案．
【详解】根据题干知：当种子粒数5000粒时，种子发芽的频率趋近于0.801，
故可以估计种子发芽的概率为0.801，到0.1，即为0.8，
故0.8．
本题比较容易，考查利用频率估计概率，大量反复试验下频率稳定值即概率．
14. 在菱形ABCD中，对角线AC，BD的长分别是6和8，则菱形的周长是____________．
【正确答案】20．

【详解】试题分析：因为菱形的对角线垂直平分，对角线AC，BD的长分别是6和8，
所以一半长是3和4，
所以菱形的边长是5，
所以周长是5×4=20．
故20．
考点：菱形的性质．
15. 如图，在Rt△ABC中，∠B＝90°，∠C＝30°，△ABC绕点A按顺时针方向旋转45°得△ADE，则∠BAE＝____________°．

【正确答案】15

【详解】由旋转的性质得，∠CAE=45°，因为∠CAB=60°，所以∠BAE=∠CAB-∠CAE=60°-45°=15°，故答案为15.
16. 如图，在Rt△ABC中，∠C＝90°，将△ABC绕点C顺时针旋转90°得到△A′B′C，M、M′分别是AB、A′B′的中点，若AC＝4，BC＝2，则线段MM′的长为____．


【正确答案】

【详解】连接MC，M′C



根据勾股定理可求得AB=A′B′=，
根据旋转没有变性，可知∠MCM′=90°，
根据直角三角形斜边上的中线等于斜边的一半，
可知CM=AB=，CM′=，
所以再次根据勾股定理可求得MN=
故
此题主要考查了直角三角形斜边上的中线，解题时先根据勾股定理求出斜边的长，然后根据旋转的性质和直角三角形的斜边上的中线求出CM、CM′，然后根据勾股定理可求解
17. 已知平面上四点，，，，直线将四边形分成面积相等的两部分，则的值为_______________．
【正确答案】

【详解】由ABCD四点坐标可得，四边形ABCD为矩形
所以，能将矩形ABCD分成面积相等的两部分的直线必须矩形对角线的交点
即线段AC和线段BD的交点（暂设它为E），
因为矩形的对角线互相平分，
所以E点为BD中点，
在Rt三角形ABD中，
根据中位线定理，得E（5，3）
把E（5，3）代入函数，得
3=5-3+2
解得=0.5
18. 如图，在□ABCD中，BC=2AB，CE⊥AB于E，F为AD的中点，若∠AEF=54°，
则∠B=_________．

【正确答案】72°

【详解】过F作FG∥AB，交BC于G，连接EG.则四边形ABGF是平行四边形，所以AF=BG，即G是BC的中点；在Rt△BEC中，EG是斜边上的中线，则BG=GE=FG=BC；∵AE∥FG，∴∠EFG=∠AEF=∠FEG=54°，∴∠AEG=∠AEF+∠FEG=108°，∴∠B=∠BEG=180°-108°=72°．故选D．

三、解答：（共74分）
19. 计算：
（1）
（2）
【正确答案】(1) ;(2)

【详解】整体分析：
（1）把除法转化乘法后，再约分化简；（2）化异分母加减为同分母加减后，再计算.
解：（1）
=
=；
（2）原式=
=
.
20. 先化简（1－ ）÷，再从﹣1，1，0，2四个数中，选一个恰当的数作为a的值代入求值．
【正确答案】

【详解】整体分析：
先计算括号内的，把除法转化为乘法后，约分化简，再选取使原分式有意义的a的值代入求值.
解：
=
.
因为当x=0，±1时，原分式无意义，所以取a=2.
当时，原式=.
21. 解方程：
（1）
（2）
【正确答案】(1)x=-2；(2)无解.

【详解】整体分析：
去分母化分式方程为整式方程，求出整式方程的解后，要把求出的解代入到公分母中检验.
解：（1）
去分母得2x=x-2，
移项合并同类项得x=-2，
经检验，x=-2是原方程的解.
（2）
去分母得3-x+1=x-4，
移项合并同类项得-2x=-8，
系数化为1得x=4.
经检验，x=4没有是原方程的解，所以原方程无解.
22. 如图，在▱ABCD中，E、F为对角线BD上的两点，且AE⊥BD，CF⊥BD．
求证：BE=DF．

【正确答案】证明见解析

【详解】试题分析：∵在平行四边形ABCD中，AB＝CD，AB∥CD，
∴∠ABE＝∠CDF．
又∵∠BAE＝∠DCF，∴△ABE≌△CDF（ASA），
∴BE＝DF．
考点：平行四边形性质
23. 已知的三个顶点的坐标分别为、、

（1）画出关于坐标原点成对称的；
（2）将绕坐标原点顺时针旋转，画出对应的；
（3）若以、、、为顶点的四边形为平行四边形，则在第四象限中的点坐标为__________．
【正确答案】（1）见解析；（2）见解析；（3）

【分析】（1）根据关于原点对称的点的横坐标与纵坐标都互为相反数解答；
（2）根据网格结构找出点A、B、C绕坐标原点顺时针旋转，得到然后顺次连接即可；
（3）根据平行四边形的对边平行且相等解答．
【详解】（1）（2）如图所示：、为所求

（3）∵、、
∴、、
∴
∴
∵
∴
故（6，-3）
本题考查了图形的旋转、平行四边形的判定等知识.熟练掌握图形的有关性质是解题的关键.
24. “摩拜单车”公司无锡市民对其产品了解情况，随机抽取部分市民进行问卷，结果分“非常了解”、“比较了解”、“一般了解”、“没有了解”四种类型，分别记为A、B、C、D．根据结果绘制了如下尚没有完整的统计图．

（1）本次问卷共随机了　 　名市民，扇形统计图中m＝　 　．
（2）请根据数据信息补全条形统计图．
（3）扇形统计图中“D类型”所对应的圆心角的度数是　 　．
（4）从这次接受的市民中随机抽查一个，恰好是“没有了解”的概率是　 　．
【正确答案】（1）50，m=32;(2)见解析；（3）43.2o；（4）

【详解】整体分析：
（1）由类型A对应的人数和所占的百分比求的人数，计算出类型D所占的百分比；（2）计算出类型B的人数；（3）类型D占人数的比乘以360°；（4）由概率的定义计算类型D的人数除以的人数.
解：（1）本次问卷共随机了8÷16%=50名市民；因为×=32%，所以m=32.
（2）因为50-8-16-6=20，所以补全的图形为：

（3）扇形统计图中“D类型”所对应的圆心角的度数是.
（4）从这次接受的市民中随机抽查一个，恰好是“没有了解”的概率是=.
25. 小军家距学校5千米，原来他骑自行车上学，学校为保障学生，新购进校车接送学生.若校车的速度是他骑车速度的2倍，则现在小军乘校车上学可以从家晚10分钟出发，结果与原来到校时间相同，试求小军骑车的速度.
【正确答案】15

【详解】整体分析：
设骑车的速度是x千米/时，用含x的式子表示骑自行车到校的时间与乘校车到校的时间，用等量关系“现在小军乘校车上学可以从家晚10分钟出发，结果与原来到校时间相同”列方程求解.
设骑车的速度是x千米/时，则校车的速度是2x千米/时，
根据题意,
解得，x＝15.
经检验：x＝15是该方程的解且符合题意.
答：小军骑车的速度是每小时15千米
26. 邻边没有相等的平行四边形纸片，剪去一个菱形，余下一个四边形，称为次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；……依次类推，若第n次操作余下的四边形是菱形，则称原平行四边形为n阶准菱形，如图1，平行四边形中，若，则平行四边形为1阶准菱形．

（1）判断与推理：
① 邻边长分别为2和3的平行四边形是__________阶准菱形；
② 小明为了剪去一个菱形，进行如下操作：如图2，把平行四边形沿着折叠（点在上）使点落在边上的点，得到四边形，请证明四边形是菱形．
（2）操作、探究与计算：
① 已知平行四边形的邻边分别为1，裁剪线的示意图，并在图形下方写出的值；
② 已知平行四边形的邻边长分别为，满足，请写出平行四边形是几阶准菱形．
【正确答案】（1）① 2，②证明见解析；
（2）①见解析，②▱ABCD是10阶准菱形．

【分析】（1）①根据邻边长分别为2和3的平行四边形两次操作，即可得出所剩四边形是菱形，即可得出答案；②根据平行四边形的性质得出AE∥BF，进而得出AE=BF，即可得出答案；
（2）①利用3阶准菱形的定义，即可得出答案；②根据a=6b+r，b=5r，用r表示出各边长，进而利用图形得出▱ABCD是几阶准菱形．
【小问1详解】
解：①利用邻边长分别为2和3的平行四边形两次操作，所剩四边形是边长为1的菱形，
故邻边长分别为2和3的平行四边形是2阶准菱形；
故2；
②由折叠知：∠ABE=∠FBE，AB=BF，
∵四边形ABCD是平行四边形，
∴AE∥BF，
∴∠AEB=∠FBE，
∴∠AEB=∠ABE，
∴AE=AB，
∴AE=BF，
∴四边形ABFE是平行四边形，
∴四边形ABFE是菱形；
【小问2详解】
解：①如图所示：
，
②答：10阶菱形，
∵a=6b+r，b=5r，
∴a=6×5r+r=31r；
如图所示：

故▱ABCD是10阶准菱形．
此题主要考查了图形的剪拼以及菱形的判定，根据已知n阶准菱形定义正确将平行四边形分割是解题关键．
27. 如图，在直角坐标系中， B（0，8），D（10，0），函数y=x+的图象过C（16，n），与x轴交于A点．
（1）求证：四边形ABCD为平行四边形；
（2）将△AOB绕点O顺时针旋转，旋转得△A1OB1，问：能否使以点O、A1、D、B1为顶点的四边形是平行四边形？若能，求点A1的坐标；若没有能，请说明理由；

【正确答案】（1）见解析；（2）能，所求满足条件的A1为：（―，）、、（，―）

【详解】整体分析：
（1）把点过C（16，n）代入到y=x+，求出n，得到点C的坐标，求出点A的坐标，由AD与BC平行且相等证明；（2）分三种情况讨论，有两种是A1B1与OD平行，一种是A1B1与OD相交，平行四边形的性质和勾股定理求解.
解：（1）∵y=x+的图象过C（16，n），A两点，∴n=×16+=8，
∴C（16，8），A（－6，0）.
∵B（0，8），∴BD∥x轴，
又∵AD=10―（―6）=16=BC，
∴四边形ABCD为平行四边形
（2）由题意可知；AB=A1B1=10，∠AOB=∠A1OB1=90°
①△AOB旋转后，若A1B1∥x轴，构成四边形OA1B1D如图①
又∵A1B1=OD=10，∴四边形OA1B1D构成平行四边形，
此时，设A1B1与y轴交于H，
则OH==，A1H==，
∴A1（―，）.

②△AOB旋转后，若A1B1的中点E在x轴上，构成四边形OA1DB1如图②.
∵∠A1OB1=90°，∴OE=A1B1=5，∴OE=ED=5，
∴四边形OA1DB1构成平行四边形，
设作A1N⊥x轴交于N，∠A1OB1=∠OA1D=90°.
则AN==，ON==，
∴A1.

③△AOB旋转后，若A1B1∥x轴，构成四边形ODA1B1如图③，
又∵A1B1=OD=10，∴四边形ODA1B1构成平行四边形，
此时，设A1B1与y轴交于M，
则OM==，A1M==，
∴A1（，―）.

综上所述，所求满足条件的A1为（―，）、、（，―）