2021-2022学年江苏省连云港市灌南高级中学高一上学期第四次考试数学试题（解析版）

这是一份2021-2022学年江苏省连云港市灌南高级中学高一上学期第四次考试数学试题（解析版），共16页。试卷主要包含了单选题，多选题，填空题，双空题，解答题等内容，欢迎下载使用。
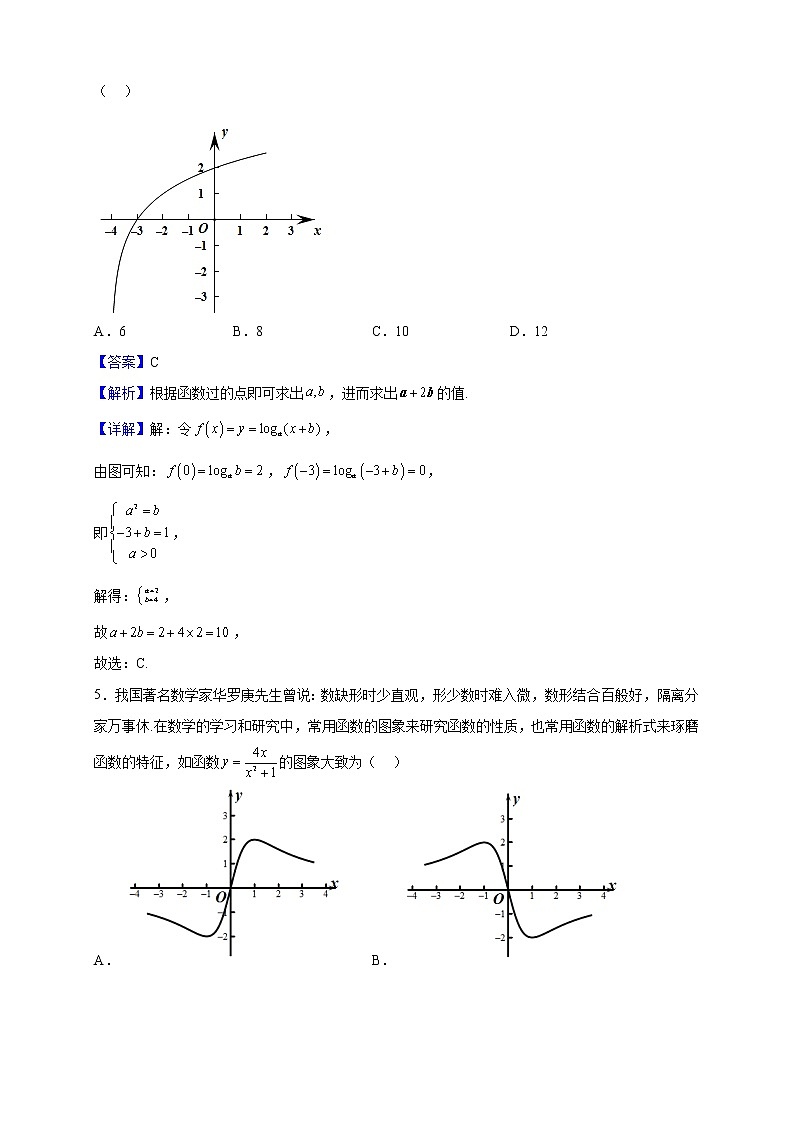
2021-2022学年江苏省连云港市灌南高级中学高一上学期第四次考试数学试题 一、单选题1．设集合， ，则（    ）A． B． C． D．【答案】A【解析】根据集合的补集、并集运算即可得到结论．【详解】解：，， ，故选：．【点睛】本题主要考查集合的基本运算，属于基础题．2．命题“，”的否定为（    ）A．， B．，C．， D．，【答案】D【分析】根据全称命题的否定，改量词、否结论，即可得出结果.【详解】命题“，”的否定为“，”.故选：D.3．设是定义在上的奇函数，当时，，则A． B． C． D．【答案】A【详解】试题分析：因为当时，，所以. 又因为是定义在R上的奇函数，所以. 故应选A.【解析】函数奇偶性的性质.4．设a与b均为实数，且，已知函数的图象如图所示，则的值为（    ）A．6 B．8 C．10 D．12【答案】C【解析】根据函数过的点即可求出，进而求出的值.【详解】解：令，由图可知：，，即，解得：，故，故选：C.5．我国著名数学家华罗庚先生曾说：数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休.在数学的学习和研究中，常用函数的图象来研究函数的性质，也常用函数的解析式来琢磨函数的特征，如函数的图象大致为（    ）A． B．C． D．【答案】A【解析】先根据，判断出函数的奇偶性，再根据函数值即可判断.【详解】解：的定义域为关于原点对称，，为上的奇函数，又时，.故选：A.6．已知函数，则（    ）A． B．-1 C．0 D．1【答案】D【分析】先求得，然后求得.【详解】，.故选：D7．高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的美誉，用其名字命名的“高斯函数”：设，用表示不超过的最大整数，则称为高斯函数，也称取整函数，例如：，．已知，则函数的值域为（    ）A． B．, C．,, D．,0,【答案】C【分析】先化简的解析式，利用不等式的性质，求出函数的值域，可得函数的值域．【详解】解：，，0,，,，故函数的值域为,,，故选：C．8．已知定义域为的奇函数又是减函数，且则的取值范围是（    ）A．  B． C． D．【答案】B【分析】先根据奇偶性将变形为，再根据函数单调性解不等式即可得答案.【详解】解：根据题意得，又因为是定义域为上的减函数，所以有：解得：故选：B．【点睛】本题考查利用函数单调性与就解不等式问题，考查数学运算能力，是中档题. 二、多选题9．下列说法正确的是（    ）A．若，则 B．若，，则C．若，，则 D．若，，则【答案】BD【解析】利用不等式的性质可判断A、B、C，利用作差法可判断D.【详解】当时，选项A不成立若，，则，故B正确当时满足，但不满足，故C不成立若，，则，故D成立故选：BD10．已知幂函数的图象经过点，则下列命题正确的有（    ）A．该函数在定义域上是偶函数B．对定义域上任意实数，，且，都有C．对定义域上任意实数，，且，都有D．对定义域上任意实数，，都有【答案】BC【分析】求出函数，可求得定义域不关于原点对称，从而可判断选项A；由函数为增函数，即可判断选项B；作差判断符合，即可判断选项C；计算与，即可判断选项D．【详解】解：因为幂函数的图象经过点，所以，所以，所以，定义域为,，为非奇非偶函数，故A错误；由幂函数的性质可知在,上为增函数，所以对任意实数，,，不妨设，则，所以，，所以，故B正确；任意实数，,，不妨设，则，又，所以，即，所以，故C正确．，，所以与不一定相等，故D错误．故选：BC．11．下列选项正确的是（    ）A．若函数，则函数在上是奇函数B．若函数是奇函数，则C．若函数，则，，且，恒有D．若函数，，，且，恒有【答案】ABD【解析】利用函数性质对选项进行判断得解【详解】选项A:由奇函数定义，正确选项B:由奇函数性质，正确选项C:，因为是增函数，由函数性质得是增函数，故错误选项D:由是下凸函数，由下凸函数性质，，且，恒有,知正确故选：ABD【点睛】熟练运用函数性质是解题关键.12．某医药研究机构开发了一种新药，据监测，如果患者每次按规定的剂量注射该药物，注射后每毫升血液中的含药量y（微克）与时间t（小时）之间的关系近似满足如图所示的曲线．据进一步测定，当每毫升血液中含药量不少于0.125微克时，治疗该病有效，则（    ）A．B．注射一次治疗该病的有效时间长度为6小时C．注射该药物小时后每毫升血液中的含药量为0.4微克D．注射一次治疗该病的有效时间长度为时【答案】AD【分析】利用图象分别求出两段函数解析式，再进行逐个分析，即可解决．【详解】由函数图象可知，当时，，即，解得，，故正确，药物刚好起效的时间，当，即，药物刚好失效的时间，解得，故药物有效时长为小时，药物的有效时间不到6个小时，故错误，正确；注射该药物小时后每毫升血液含药量为微克，故错误，故选：． 三、填空题13．_________.【答案】3【分析】直接利用换底公式计算得到答案.【详解】原式.故答案为：.【点睛】本题考查了换底公式，意在考查学生的计算能力和转化能力.14．已知函数若，则的取值范围为             ．【答案】．【详解】试题分析：分类讨论：若，则，解得，所以；若，则，解得；综上，．【解析】分段函数．15．若函数(且)，满足对任意的､，当时，，则实数a的取值范围为______.【答案】【解析】由题意可知，函数在上单调递减，利用复合函数的单调性分析出外层函数的单调性，再由可得出关于实数的不等式组，由此可解得实数的取值范围.【详解】由题意可知，函数在上单调递减，由于内层函数在区间上单调递减，所以，外层函数单调递增，则，且当时，恒成立，即，，解得.因此，实数的取值范围是.故答案为：.【点睛】关键点点睛：解本题的关键点：（1）利用复合函数的单调性“同增异减”分析出内层函数和外层函数的单调性； （2）不要忽略了真数要恒大于零. 四、双空题16．设正数x，y满足，则的最小值为________；此时的值为________．【答案】          1【解析】，然后利用基本不等式求解即可.【详解】因为，所以所以所以，当且仅当，即时等号成立，此时故答案为：；1 五、解答题17．已知函数，的值域为集合，关于的不等式的解集为，集合，集合．（1）若，求实数的取值范围；（2）若，求实数的取值范围．【答案】（1）；（2）．【分析】（1）根据指数函数性质，先求出，解指数不等式，求出，根据得，由此列出不等式求解，即可得出结果；（2）先解分式不等式，求出，根据，分别讨论，两种情况，即可得出结果.【详解】（1）由对数函数的单调性可得，在上单调递增，所以其值域，又由可得：，即：，所以，所以，又所以可得：，所以，所以，即实数的取值范围为．（2）因为，所以有，所以，所以，对于集合有：①当时，即时，满足；②当时，即时，所以有：，又因为，所以，综上：由①②可得：实数的取值范围为．【点睛】本题主要考查由并集的结果求参数，考查由集合的包含关系求参数，涉及指数函数与对数函数的性质，以及分式不等式解法，属于常考题型.18．在①，②，③这三个条件中任选一个，补充在下面的横线上，并回答下列问题．设全集，____，,．(1)当时，求，；(2)若“”是“”的充分不必要条件，求实数的取值范围．【答案】(1)，或(2) 【分析】（1）直接利用集合交集、并集、补集的定义求解即可；（2）利用充分条件和必要条件的定义将问题转化为集合的真子集关系，列出不等式组，求解即可．【详解】（1）解：若选①：，当时，，，所以，或；若选②：，当时，，，所以，或；若选③：，（1）当时，，，所以，或；（2）解：若“”是“”的充分不必要条件，则有,，则有（不能同时取等号），解得，故实数的取值范围为．19．已知函数.（1）当时，解不等式；（2）若函数的图象过点，且关于的方程有实根，求实数的取值范围.【答案】（1）；（2）.【分析】（1）当时，解指数、对数不等式求得不等式的解集.（2）利用求得，由分离常数，利用构造函数法，结合函数的值域，求得的取值范围.【详解】（1）当时，.由，得，得，得，解得.故不等式的解集是.（2）因为函数的图象过点，所以，即，解得.所以.因为关于的方程有实根，即有实根.所以方程有实根..令，则.因为，，所以的值域为.所以，解得.所以实数的取值范围是.【点睛】研究方程的零点问题，可考虑分离常数法，结合函数值域进行求解.20．沪苏合作的长三角（东台）康养小镇项目正式落户江苏盐城东台——月日，该项目在南京举办签约仪式，该项目由盐城市政府、东台市政府和上海地产集团合作共建，选址在东台沿海经济区，总占地平方公里，其中一期平方公里，规划人口万人，总投资亿元，定位于长三角区域康养服务一体化示范区、跨行政区康养政策协同试验区．此消息一出，众多商家目光投向东台．某商家经过市场调查，某商品在过去天内的销售量（单位：件）和价格（单位：元）均为时间t（单位：天）的函数，且销售量近似地满足．前天价格为，后天价格为．（1）试写出该种商品的日销售额与时间的函数关系式；（2）求出该商品的日销售额的最大值．【答案】（1）；（2）元．【解析】（1）由可得出与的函数关系式；（2）利用二次函数以及分段函数的基本性质可求得的最大值.【详解】（1）当且，；当且时，.因此，；（2）当且时，二次函数的图象开口向下，对称轴为直线，；当且时，二次函数的图象开口向上，对称轴为直线，此时，随的增大而减小，．又，．答：该商品的日销售额的最大值为元．【点睛】思路点睛：解函数应用题的一般程序：第一步：审题——弄清题意，分清条件和结论，理顺数量关系；第二步：建模——将文字语言转化成数学语言，用数学知识建立相应的数学模型；第三步：求模——求解数学模型，得到数学结论；第四步：还原——将用数学方法得到的结论还原为实际问题的意义；第五步：反思回顾——对于数学模型得到的数学结果，必须验证这个数学解对实际问题的合理性．21．已知f(x)+g(x)＝log2（2﹣x），其中f(x)为奇函数，g(x)为偶函数．(1)求f(x)与g(x)的解析式；(2)判断函数f(x)在其定义域上的单调性；(3)解关于t不等式f（t﹣1）+f（2t+1）﹣3t＞0．【答案】(1)f(x)=log2，g(x)=log2（4-x2）(2)f(x)在（-2，2）上单调递减(3)（-1，0） 【分析】（1）由，分别是奇偶函数，将“”代入，利用奇偶函数的性质，解方程得，的解析式；（2）求的定义域，整理内层函数，利用复合函数的单调性原则判断单调性；（3）观察不等式，构造函数，易得的奇偶性和单调性，解不等式.【详解】（1）由于函数f(x)为奇函数，g(x)为偶函数，可得f（-x）=-f(x)，g（-x）=g(x)，因为f(x)+g(x)=log2（2-x），所以f（-x）+g（-x）=log2（2+x），即-f(x)+g(x)=log2（2+x），解得，．（2）的定义域为（-2，2），且，因为在（-2，2）上单调递减，是增函数，由复合函数的单调性可知f(x)在（-2，2）上单调递减．（3）令h(x)=f(x)-x，，由h（-x）=f（-x）+x=-f(x)+x=-h(x)，可得h(x)为奇函数，且在（-2，2）上单调递减，因为f（t-1）+f（2t+1）-3t＞0，所以f（t-1）-（t-1）+f（2t+1）-（2t+1）＞0，即h（t-1）+h（2t+1）＞0，即h（t-1）＞-h（2t+1）=h（-2t-1），所以 ，解得-1＜t＜0，不等式解集为.22．已知函数，其中.（1）当函数为偶函数时，求m的值；（2）若，函数，，是否存在实数k，使得的最小值为0？若存在，求出k的值，若不存在，说明理由；（3）设函数，，若对每一个不小于3的实数，都有小于3的实数，使得成立，求实数m的取值范围.【答案】（1）；（2）；（3）【解析】（1）由可得m的值；（2）当时，，令，则，分类讨论求出的最小值，列方程即可求解；（3）将题目的条件转化为：对于任意一条直线，如果与图象中满足的部分图象有交点，则必然与的图象中满足的部分图象也有交点，分四种情况讨论即可得实数m的取值范围.【详解】（1）当函数为偶函数时，，所以，解得：，经检验，符合，故；（2）当时，，令，则，当即时，在上单调递增，所以，解得：，符合；当即时，无解；当即时，在上单调递减，所以，解得：，应舍去；综上，；（3），将题目的条件转化为：对于任意一条直线，如果与图象中满足的部分图象有交点，则必然与的图象中满足的部分图象也有交点.当时，是单调递增的，所以当时，是单调函数，分四种情况讨论：①当时，在上符号是负，而在上符号是正的，所以不满足题目的条件；②当时，当时，，而当时，，所以也不符合条件；③当时，要满足条件只需即，所以；④当时，要满足条件只需即，即，令，因为在上单调递增，且，所以解得，所以，综上，实数m的取值范围为.【点睛】关键点睛：本题的关键是能够将题目的条件转化为：对于任意一条直线，如果与图象中满足的部分图象有交点，则必然与的图象中满足的部分图象也有交点，结合图象就能求解出实数m的取值范围；当然再分析当情况时，需要构造函数，利用单调性求解不等式.