2021-2022学年江苏省无锡市太湖高级中学高一上学期12月阶段性测试数学试题（解析版）

这是一份2021-2022学年江苏省无锡市太湖高级中学高一上学期12月阶段性测试数学试题（解析版），共14页。试卷主要包含了单选题，多选题，填空题，双空题，解答题等内容，欢迎下载使用。
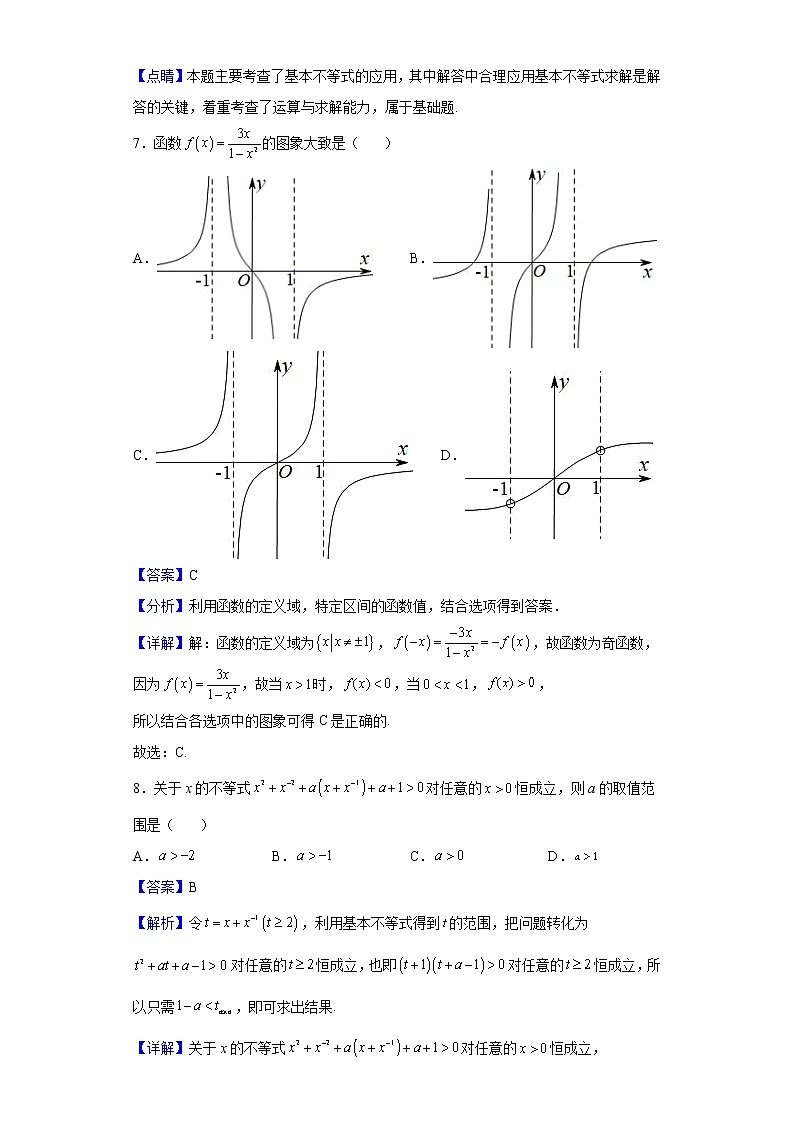
2021-2022学年江苏省无锡市太湖高级中学高一上学期12月阶段性测试数学试题一、单选题1．设集合， ， ，则A．{2} B．{2，3} C．{-1，2，3} D．{1，2，3，4}【答案】D【分析】先求，再求．【详解】因为，所以.故选D．【点睛】集合的运算问题，一般要先研究集合中元素的构成，能化简的要先化简，同时注意数形结合，即借助数轴、坐标系、韦恩图等进行运算．2．函数的图象恒过定点（       ）A． B．C． D．【答案】B【分析】根据指数函数的图象过定点及函数图象变换求解即可.【详解】解：因为指数函数图象向左平移个单位，再向上平移个单位即可得到函数的图象，指数函数过定点，所以函数的图象恒过定点.故选：B3．已知，那么用表示是（       ）A． B． C． D．【答案】A【分析】根据指数与对数的关系及对数的性质计算可得；【详解】解：因为，所以所以==，故选：A．4．已知角的终边经过点，那么（       ）A．-2 B． C． D．2【答案】C【分析】根据三角函数终边上点的定义求解即可.【详解】解：因为角的终边经过点，所以，所以.故选：C5．已知，，，则（       ）A． B． C． D．【答案】A【分析】根据指数函数、幂函数和对数函数的单调性，结合临界值和可确定的大致范围，从而得到结果.【详解】，即本题正确选项：【点睛】本题考查根据指数函数、幂函数和对数函数单调性比较大小的问题，解决此类题的常用方法是利用临界值来确定所比较数字的大致范围.6．已知，，若，则A．有最小值 B．有最小值C．有最大值 D．有最大值【答案】A【分析】根据基本不等式的性质，即可求解有最小值，得到答案.【详解】由题意，可知，，且，因为，则，即，所以，当且仅当时，等号成立，取得最小值，故选A．【点睛】本题主要考查了基本不等式的应用，其中解答中合理应用基本不等式求解是解答的关键，着重考查了运算与求解能力，属于基础题.7．函数的图象大致是（       ）A． B．C． D．【答案】C【分析】利用函数的定义域，特定区间的函数值，结合选项得到答案．【详解】解：函数的定义域为，，故函数为奇函数，因为，故当时，，当，，所以结合各选项中的图象可得C是正确的.故选：C.8．关于x的不等式对任意的恒成立，则a的取值范围是（       ）A． B． C． D．【答案】B【解析】令，利用基本不等式得到的范围，把问题转化为对任意的恒成立，也即对任意的恒成立，所以只需，即可求出结果.【详解】关于x的不等式对任意的恒成立，即对任意的恒成立，令，当且仅当时取等号；则对任意的恒成立，也即对任意的恒成立，所以只需，所以，即．故选：B．【点睛】关键点睛：令，利用基本不等式得到的范围，把问题转化为对任意的恒成立是解决本题的关键.二、多选题9．下列说法正确的有（       ）A．不等式的解集是B．“，”是“”成立的充分不必要条件C．命题：，，则：，D．【答案】AB【分析】解分式不等式可知A正确；由充分条件和必要条件的定义，可得B正确；含有全称量词命题得否定，，故C错误；结合指数幂的运算求解判断D选项.【详解】解：对于A选项，由，即，，A正确；对于B选项，时一定有，但时不一定有成立,因此“”是“”成立的充分不必要条件，B正确；对于C选项，命题，则，C错误；对于D选项，，故错误.故选：AB．10．已知幂函数的图象经过点.则（　　）A．的定义域为 B．的值域为C．是偶函数 D．的单调增区间为【答案】ABD【解析】先求出幂函数的解析式，再根据解析式判断各项的正误.【详解】因为为幂函数，故，所以，故，故，所以函数的定义域为，值域为，单调增区间为，且不是偶函数，故选：ABD.11．下列结论中正确的是（       ）A．终边经过点的角的集合是；B．将表的分针拨慢10分钟，则分针转过的角的弧度数是；C．若是第三象限角，则是第二象限角，为第一或第二象限角；D．，，则【答案】ABD【分析】直接以角的表示方法，象限角的概念，集合间的关系求出结果.【详解】A.终边经过点的角的终边在第一象限平分线上，故角的集合是，所以A正确；B. 将表的分针拨慢10分钟，按逆时针旋转，则分针转过的角度为，对应弧度数是，所以B正确；C.因为是第三象限角，即，所以，当为奇数时，是第四象限角，当为偶数时，是第二象限角；，所以的终边位置在第一或第二象限或轴非负半轴，所以C错误；D. ，，易知，所以D正确；故选：ABD.12．高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设，用表示不超过的最大整数，则称为高斯函数，例如：，．已知函数，则关于函数的叙述中正确的是（       ）A．是偶函数 B．是奇函数C．在上是增函数 D．的值域是【答案】BC【解析】计算得出判断选项A不正确；用函数的奇偶性定义，可证是奇函数，选项B正确；通过分离常数结合复合函数的单调性，可得出在R上是增函数，判断选项C正确；由的范围，利用不等式的关系，可求出，选项D不正确，即可求得结果.【详解】根据题意知，.∵，，，∴函数既不是奇函数也不是偶函数，A错误；，∴是奇函数，B正确；在R上是增函数，由复合函数的单调性知在R上是增函数，C正确；，，， ，，D错误.故选：BC.【点睛】关键点睛：本题是一道以数学文化为背景，判断函数性质的习题，属于中档题型，本题的关键是理解函数，然后才会对函数变形，并作出判断.三、填空题13．计算：_____.【答案】8【分析】根据指数、对数的运算性质进行计算即可.【详解】故答案为：8．14．若关于的方程有两个实数根，且一根大于1，另一根小于1，则实数的取值范围为___________.【答案】【分析】令，根据题意，由求解.【详解】令，因为方程有两个实数根，且一根大于1，另一根小于1，所以，解得，所以实数的取值范围为，故答案为：15．对于函数，若在定义域内存在实数满足，则称函数为“函数”.设为其定义域上的“函数”，则实数的取值范围是___________.【答案】【分析】由题可得：在上有解，即可转化为： 在上有解，且在上恒成立，转化为的值域且，问题得解【详解】解：由函数为“函数”的定义可得：在上有解.即：在上有解则在上有解，且在上恒成立即：在上有解，且在上恒成立记，由于函数在上均单调递增，所以在上单调递增，且所以所以，即：，解得：又在上恒成立，由对勾函数性质得在上单调递增，所以，解得：综上所述：实数的取值范围是故答案为:四、双空题16．已知，则____________；___________.【答案】          -0.1【分析】结合，将所求式子化弦为切后再将代入即可求解【详解】解：，，故答案为：；五、解答题17．已知半径为6的圆中，弦的长为6.(1)求弦所对圆心角的大小；(2)求圆心角所在的扇形的弧长及弧所在的弓形的面积【答案】(1)(2)，【分析】（1）根据三角形形状得圆心角的大小；（2）根据扇形的弧长以及面积公式求解.【详解】(1)解：半径为6的圆中，弦的长为6，所以三角形为正三角形，所以弦所对圆心角为，(2)解：由弧长公式得： 扇形的面积又，所以，即弧所在的弓形的面积.18．已知函数的定义域为集合，集合.（1）当时，求；（2）若是的必要条件，求实数的取值范围.【答案】（1）；（2）【解析】（1）先求得集合A，当时，可求得集合B，根据并集的运算法则，即可求得答案；（2）根据题意，可得，分别讨论和两种情况，根据集合的包含关系，即可求得答案.【详解】由题意得：，所以集合，（1）当时，集合，所以.（2）若是的必要条件，则，当时，，解得，符合题意，当时，则，解得，综上的取值范围为【点睛】易错点点睛：当出现，即B集合为小范围，且B集合含有参数时，需讨论B集合是否为空集，再进行求解，考查分析理解的能力，属基础题.19．已知，.(1)求角的集合：(2)求角的终边所在的象限；(3)试判断的符号.【答案】(1)(2)第二、四象限(3)正号【分析】（1）根据条件判断出所在象限，即可写出α的集合；（2）由（1）求出范围，即可判断象限；（3）根据的象限即可判断函数值正负.【详解】(1)由，知在第三、四象限或y轴的负半轴上，由，知在第二、四象限，故角在第四象限，其集合为；(2)由（1）知，故，故的终边在第二、四象限；(3)当在第二象限时，，，，所以，当在第四象限时，，，，所以，综上，取正号.20．已知函数为偶函数，为奇函数，且.(1)求函数和的解析式；(2)若在恒成立，求实数的取值范围.【答案】(1)；(2).【分析】（1）根据函数为偶函数，为奇函数，结合求解；（2）将在恒成立，转化为在恒成立求解.【详解】(1)解：因为函数为偶函数，为奇函数，所以，又，则，即，两式联立解得；(2)由（1）知：，因为在恒成立，所以在恒成立，令，则，由对勾函数的性质得函数y在上递增，所以，所以，所以实数的取值范围.21．科技创新在经济发展中的作用日益凸显．某科技公司为实现9000万元的投资收益目标，准备制定一个激励研发人员的奖励方案：当投资收益达到3000万元时，按投资收益进行奖励，要求奖金（单位：万元）随投资收益（单位：万元）的增加而增加，奖金总数不低于100万元，且奖金总数不超过投资收益的20%．（1）现有三个奖励函数模型：①，②，③，．试分析这三个函数模型是否符合公司要求？（2）根据（1）中符合公司要求的函数模型，要使奖金额达到350万元，公司的投资收益至少要达到多少万元？【答案】（1）见解析；（2）投资收益至少要达到万元【解析】（1）根据公司要求知函数为增函数，同时应满足且，一一验证所给的函数模型即可；（2）由，解不等式即可.【详解】（1）由题意符合公司要求的函数在为增函数，在且对，恒有且．①对于函数，当时，，不符合要求；②对于函数为减函数，不符合要求； ③对于函数在，显然为增函数，且当时， ；又因为；而，所以当时，．所以恒成立；因此，为满足条件的函数模型． （2）由得：，所以，所以公司的投资收益至少要达到万元．【点睛】本题主要考查的是函数模型的选择与运用，考查函数的单调性和最值以及恒成立问题，对数不等式的解法，考查学生的分析问题解决问题的能力.22．已知函数且.(Ⅰ) 若1是关于x的方程的一个解，求t的值；(Ⅱ) 当且时，解不等式；(Ⅲ)若函数在区间（-1,2]上有零点，求t的取值范围.【答案】(Ⅰ) (Ⅱ)(Ⅲ)或【详解】试题分析：（Ⅰ）由，即可求得的值；(Ⅱ)当时，当时，即，利用对数函数的单调性可得真数间的大小关系，注意对数函数的定义域；(Ⅲ)分情况讨论：若，则在上没有零点，当时，分在内有重根，则△=0,解得的值；在上只有一个零点，且不是方程的重根时；在上有两个相异实根三种情况，根据函数零点判定定理可得不等式，解出即可；试题解析：（Ⅰ）∵若1是关于的方程的解，，又.(Ⅱ)时，，又，∴解集为：；（Ⅲ）若，则在上没有零点.下面就时分三种情况讨论：方程在上有重根，则，解得；①在上只有一个零点，且不是方程的重根，则有，解得，又经检验：时，在上都有零点，.②;在上有两个相异实根，则有：或，解得，③;综合①②③可知的取值范围为或【解析】函数的零点.不等式的解法【名师点睛】本题考查函数零点判定定理、对数不等式的解法，属中档题，解对数不等式要注意考虑对数函数定义域．分情况讨论时要注意分类标准，做到不重不漏.