18.1.1 第1课时 平行四边形的边、角的特征 课件 2022-2023学年人教版数学八年级下册

这是一份18.1.1 第1课时 平行四边形的边、角的特征 课件 2022-2023学年人教版数学八年级下册，文件包含1811第1课时平行四边形的边角的特征pptx、平行四边形mp4等2份课件配套教学资源，其中PPT共26页， 欢迎下载使用。

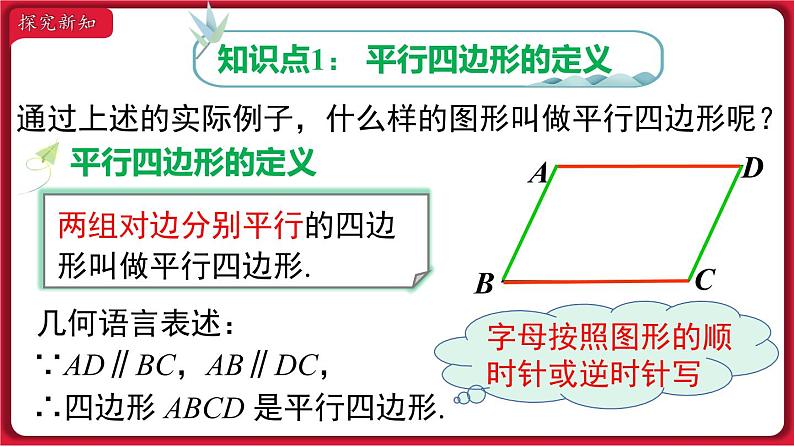
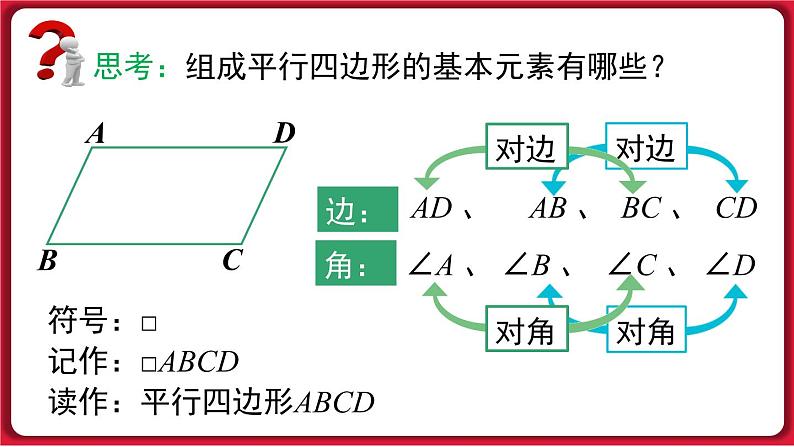
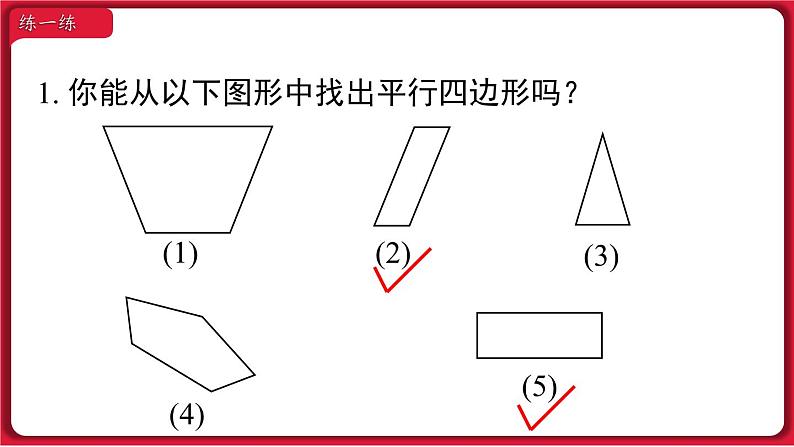
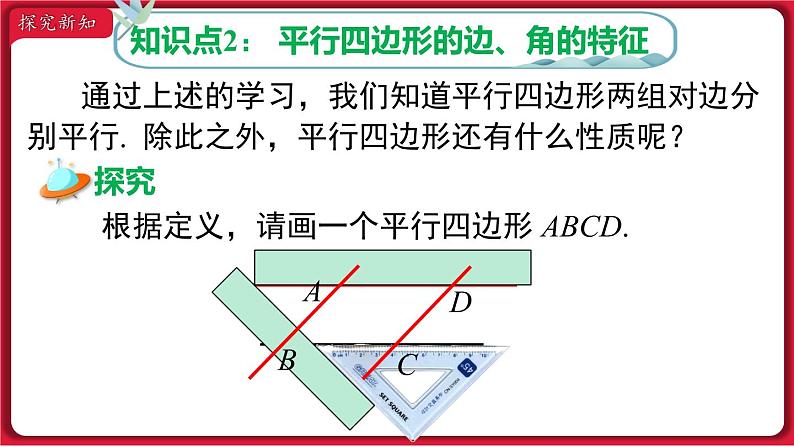
18.1.1 平行四边形的性质第十八章 平行四边形第1课时 平行四边形的边、角特征 小学我们就学过平行四边形，通过下面的视频，你还能找到类似的例子吗？点击视频开始播放→课堂导入 观察下图，平行四边形在生活中无处不在.知识点1： 平行四边形的定义 通过上述的实际例子，什么样的图形叫做平行四边形呢？两组对边分别平行的四边形叫做平行四边形.几何语言表述：∵AD∥BC，AB∥DC，∴四边形 ABCD 是平行四边形.探究新知符号：□记作：□ABCD读作：平行四边形ABCD思考：组成平行四边形的基本元素有哪些？边：角：AD 、 AB 、 BC 、 CD∠A 、 ∠B 、 ∠C 、 ∠D两组对边分别平行1. 你能从以下图形中找出平行四边形吗？(2)(3)(1)(4)(5)练一练知识点2： 平行四边形的边、角的特征 通过上述的学习，我们知道平行四边形两组对边分别平行. 除此之外，平行四边形还有什么性质呢？ 根据定义，请画一个平行四边形 ABCD. DABC探究新知ABCD活动1 请用尺子等工具度量你手中平行四边形的四条边，并记录下数据，你能发现 AB 与 DC，AD 与 BC 之间的数量关系吗?测得 AB = DC，AD = BC.ABCD测得∠A =∠C，∠B =∠D.活动2 请用量角器等工具度量你手中平行四边形的四个角，并记录下数据，你能发现∠A 与∠C，∠B 与∠D 之间的数量关系吗?∠A +∠D = 180°，∠B +∠C = 180°.ABCD活动3 请用剪刀，沿 AC 将平行四边形剪成两个三角形，你能发现这两个三角形有什么样的关系吗?( C )( A )( D )猜想 平行四边形的两组对边，两组对角有什么数量关系？ 两组对边及两组对角分别相等.怎样证明这个猜想呢？重合.已知：四边形 ABCD 是平行四边形.求证：AD = BC，AB = CD，∠BAD = ∠BCD，∠ABC = ∠ADC.1432分析：求证 AD = BC，AB = CDAD∥BC，AB∥CD连接 AC全等 AC 是公共边AD = BC，AB = CD，∠ABC =∠ADC△ABC≌△CDA∠BAD = ∠BCD逆向思维∠1 =∠2，∠3 =∠4思考：不添加辅助线，你能否直接运用平行四边形的定义，证明其对角相等？分析：AD∥BC，AB∥CD∠A +∠B = 180°，∠A +∠D = 180°∠B = ∠D ∠A =∠C 正向思维平行四边形的对边相等．平行四边形的对角相等．几何语言表述：∵ 四边形 ABCD 是平行四边形，∴ AB = CD，AD = BC， ∠A =∠C，∠B = ∠D归纳总结例1 如图，在 □ABCD 中，DE⊥AB，BF⊥CD，垂足分别是 E，F．求证：AE = CF．分析：正向思维□ABCDAD = BC，∠A =∠CDE⊥AB，BF⊥CD∠DEA =∠BFC逆向思维求证 AE = CF全等△DEA≌△BFCAB = CD，∠ABC =∠CDA典例分析证明：∵ 四边形 ABCD 是平行四边形，∴ ∠A = ∠C，AD = CB.又∠AED = ∠CFB = 90°，∴ △ADE≌△CBF (AAS)，∴ AE = CF. 例1 如图，在 □ABCD 中，DE⊥AB，BF⊥CD，垂足分别是 E，F．求证：AE = CF．思考 在上述证明中还能得出什么结论？DE = BF四边形问题三角形问题2. 如图，在□ABCD 中. (1) 若∠A = 130°，则∠B =______ ，∠C =______ ， ∠D =______. (3) 若∠A + ∠C = 200°，则∠A =_____，∠B =______. (2) 若 AB = 3，BC = 5，则它的周长 = ______. 50°130°50°100°80°16练一练知识点3： 平行线间的距离追问1 如图 a∥b，c∥d ，我们能得出 AD = BC ？ abcdDABC探究新知ab追问2 如图，直线 a∥b，D，C 为直线 a 上任意两点，点 D 到直线 b 的距离和点 C 到直线 a 的距离相等吗？FE 思考：两条平行线之间的距离和点与点之间的距离、点到直线的距离有何联系与区别？ 点与点之间的距离是定义点到直线的距离、两条平行线之间的距离的基础，它们本质都是点与点之间的距离.3. 在同一平面上，直线 a，b，c 是三条平行直线. 如果直线 a 和 b 的距离为 6，直线 b 和 c 的距离为 3， 那么直线 a 和 c 的距离为 .9 或 3练一练平行四边形定义_________________的四边形性质平行四边形的____________________两条平行线之间的任何两条平行线段都____平行四边形的___________________两组对边分别平行两组对边分别平行相等边角两条平行线间的距离：一条直线上___________到另一条直线的距离 综合应用两组对角分别相等任意一点相等课堂总结 1. 判断题 (对的在括号内填“ √ ”，错的填“×”)： (1) 平行四边形两组对边分别平行且相等. ( ) (2) 平行四边形的四个内角都相等. ( ) (3) 平行四边形的相邻两个内角的和等于 180°. ( ) (4) 如果平行四边形相邻两边长分别是 2 cm 和 3 cm，那么周长是10 cm. ( ) (5) 在平行四边形 ABCD 中，如果∠A = 42°， 那么∠B = 48°. ( )√√√××课堂练习2. 如图，直线 AE∥BD，点 C 在 BD 上， 若 AE = 5，BD = 8，△ABD 的面积为 16， 则△ACE 的面积为 .103. 如图，在 □ABCD 中，AD = 2AB，CM 平分∠BCD，交边 AD 于点 M，AM = 4，则 AD = ________. 84. 有一块形状如图所示的玻璃，不小心把 EDF 部分打碎了，现在只测得 AE = 60 cm，BC = 80 cm，∠B = 60°，且 AE∥BC，AB∥CF，你能根据测得的数据计算出 DE 的长度和∠D 的度数吗？解：∵AE∥BC，AB∥CF，∴ 四边形 ABCD 是平行四边形.∴∠D = ∠B = 60°， AD = BC = 80 cm.∴ ED = AD - AE = 20 cm.答：DE 的长度是 20 cm，∠D 的度数是 60°.能力提升5. 如图，在△ABC 中，AD 平分∠BAC，点 M、E、F 分别是 AB，AD，AC 上的点，四边形 BEFM 是平行四边形. 求证：AF = BM.证明： ∵ 四边形 BEFM 是平行四边形，∴ BM = EF，AB∥EF.∵ AD 平分∠BAC，∴ ∠BAD =∠CAD.∵ AB∥EF， ∴ ∠BAD =∠AEF.∴ ∠CAD =∠AEF， ∴ AF = EF. ∴ AF = BM.