2022-2023学年河南省洛阳市强基联盟高一上学期第一次大联考数学试题（解析版）

这是一份2022-2023学年河南省洛阳市强基联盟高一上学期第一次大联考数学试题（解析版），共10页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
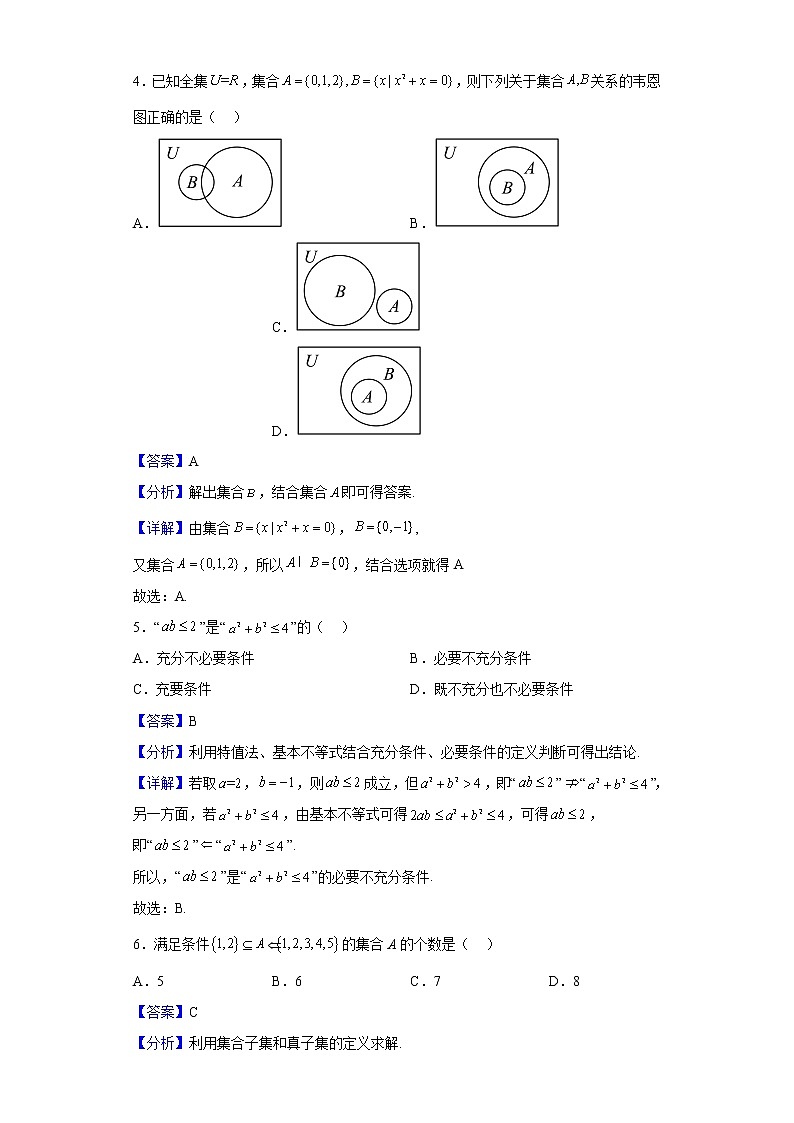
2022-2023学年河南省洛阳市强基联盟高一上学期第一次大联考数学试题 一、单选题1．已知集合，则（    ）A．{2} B．{4，5} C．{3，4} D．{2，3}【答案】B【分析】先求集合的补集，再与集合求交集即可.【详解】，  或，故选：B.2．设命题:3，则为 为（    ）A． B．C． D．【答案】A【分析】由特称命题的否定判断,【详解】由题意得为 ，3.故选：A3．不等式0的解集是（    ）A． B．C． D．【答案】D【分析】根据分式不等式的求解步骤，等价转化整式不等式，结合二次不等式，可得答案.【详解】分式不等式0等价于，即0，解得，故不等式>0的解集是.故选：D.4．已知全集，集合，则下列关于集合关系的韦恩图正确的是（    ）A． B． C． D．【答案】A【分析】解出集合，结合集合即可得答案.【详解】由集合，,又集合，所以，结合选项就得A故选：A.5．“”是“”的（    ）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件【答案】B【分析】利用特值法、基本不等式结合充分条件、必要条件的定义判断可得出结论.【详解】若取，，则成立，但，即“”“”，另一方面，若，由基本不等式可得，可得，即“”“”.所以，“”是“”的必要不充分条件.故选：B.6．满足条件的集合A的个数是（    ）A．5 B．6 C．7 D．8【答案】C【分析】利用集合子集和真子集的定义求解.【详解】因为集合，所以集合 A 可以是, , 共 7 个.故选:C.7．已知，则的最小值为（    ）A．6 B．4 C．5 D．9【答案】C【分析】将变换为，再利用基本不等式求解即可.【详解】解：．当且仅当，即x＝3时，“＝”成立．故选:C．8．已知实数，关于的不等式的解集为，则实数a、b、、从小到大的排列是(    )A． B．C． D．【答案】A【分析】由题可知，再利用中间量，根据与之间的关系求出的取值范围，即可判断a、b、、之间的关系.【详解】由题可得：，.由，，设，则.所以，所以，.又，所以，所以.故，.又，故.故选：A. 二、多选题9．下列各式中关系符号运用正确的是（    ）A． B．C． D．【答案】BC【分析】根据元素和集合的关系与集合与集合的关系逐个判断即可.【详解】解：根据元素和集合的关系知，所以A错误；根据元素和集合的关系知，所以B正确；根据集合与集合的关系知，所以C正确；根据集合与集合的关系知，所以D错误.故选：BC.10．已知或，，若是的充分不必要条件，则的取值可以是（     ）A． B． C．2 D．1【答案】AB【分析】根据充分不必要条件求出参数的取值范围，再结合选项判断即可.【详解】解：因为或，，又是的充分不必要条件，故，对比选项知AB满足条件.故选：AB.11．下列说法正确的是（     ）A．设A，B是两个不同的定点，则集合{P|PA=PB}表示的平面图形是等腰三角形B．是 (AB)的充分不必要条件C．若 ，则 D．若对0都成立，则【答案】CD【分析】由集合的概念，充分必要条件，不等式的性质，基本不等式对选项逐一判断【详解】对于A，满足，则动点P的轨迹为线段AB的中垂线，故A错误，对于B，若，则 (AB)不一定成立，故B错误，对于C，根据不等式的基本性质得，若，则是成立的，故C正确，对于D，，又0，，当且仅当时等号成立，所以，故D正确，故选：CD12．对任意集合，记，则称为集合的对称差，例如，若{0，1，2}，{1，2，3}，则={0，3}，下列命题中为真命题的是（    ）A．若且AB=，则A=BB．若且AB=B，则A=C．存在，使得AB=D．若且 ABA，则【答案】ABC【分析】根据对称差的定义及交、并、补运算，逐项判断即可．【详解】A．因为AB=，所以=且，即AB与AB是相同的，所以A=B，故本选项符合题意；B．因为AB=B，所以B=，所以AB，且B中的元素不能出现在AB中， 因此A=，故本选项符合题意；C．A=B时，AB=，==AB，故本选项符合题意； D．因为ABA，所以，所以BA，故本选项不符合题意．故选：ABC．【点睛】本题的难点是要经过转化才能得到常见的集合关系，对新定义要有准确的理解：本质上就是求两个集合交集在二者并集上的补集，可借助韦恩图辅助理解． 三、填空题13．若，则M与N的大小关系为__________    .【答案】【分析】作差法比较大小即可.【详解】因为 ，所以.故答案为: .14．某班共40人，其中24人喜欢篮球运动，13人喜欢乒兵球运动，6人这两项运动都不喜欢，则只喜欢乒乓球运动的人数为_________.【答案】10【分析】设喜欢篮球运动、乒乓球运动的学生构成的集合分别为，，全集为，设这两项运动都喜欢的有人，根据题意画出图，利用图即可求解．【详解】解：设喜欢篮球运动、乒乓球运动的学生构成的集合分别为，，全集为，设这两项运动都喜欢的有人，由题意可得图，如图所示，故，解得，故只喜欢乒乓球运动的人数为．故答案为：10.15．命题“”假命题，则取值范围为___________.【答案】【分析】利用命题与命题的否定一真一假得到为真命题，进而结合二次函数图象可求解.【详解】p为假命题， = 0为真命题，，解得，，故答案为:.16．已知，，则的最大值是_______．【答案】【分析】令，，化简原式，然后利用基本不等式即可求解.【详解】解：令，，则，．因为，，所以，，所以，当且仅当时取等号，所以的最大值是.故答案为：. 四、解答题17．已知集合，且.(1)求实数的取值的集合；(2)写出（1）中集合的所有子集.【答案】(1)；(2) 【分析】（1）利用可求出，再验证合理性，进一步确定值；（2）利用子集的概念作答即可【详解】(1)因为，且，所以或，解得或或，当时，，集合中出现两个0，故舍去；当时，，符合题意；当时，，符合题意；∴实数的取值的集合(2)因为，所以集合的子集有：18．已知 ，.(1)当 时，求 ;(2)若，求实数的取值范围.【答案】(1)(2){或4} 【分析】（1）时，可以求出集合，然后进行并集的运算即可；（2）求解，根据，列不等式即可得出实数的取值范围．【详解】(1)解：当时所以(2)解： ，.或.，4，故的取值范围为{或4}19．设.(1)若，求同时满足条件的实数构成的集合;(2)若是的充分条件，求实数的取值范围.【答案】(1)(2) 【分析】(1)求集合的交集即可;(2)利用集合的包含关系可求解.【详解】(1)由解得，所以,当 =2 时，即 ，所以,    所以同时满足条件的实数构成的集合即为公共部分的实数构成的集合，即为 ；(2)因为p是q的充分条件，且，,,所以 ，所以，解得0，故实数的取值范围是.20．求证下列问题：(1)已知均为正数，求证:.(2)已知，求证: 的充要条件是.【答案】(1)证明见解析(2)证明见解析 【分析】（1）结合基本不等式证得不等式成立.（2）结合不等式的性质、差比较法以及充要条件的知识证得结论成立.【详解】(1)，当且仅当，即时等号成立.(2)依题意，则或，所以：，所以：的充要条件是.21．已知集合 ，，且．(1)若命题p：“，”是真命题，求实数m的取值范围；(2)若命题q：“，”是真命题，求实数m的取值范围．【答案】(1)(2) 【分析】（1）由命题p：“，”是真命题，可知，根据子集的含义解决问题；（2）命题q：“，”是真命题，所以，通过关系解决.【详解】(1)由命题p：“，”是真命题，可知，又，所以 ，解得．(2)因为，所以，得．因为命题q：“，”是真命题，所以，所以，或，得．综上，．22．第31届世界大学生夏季运动会将于2023年7月28日至8月8日在四川成都举行，某公司为了竞标配套活动的相关代言，决定对旗下的某商品进行一次评估.该商品原来每件售价为25元，年销售 8万件.(1)据市场调查，若价格每提高1元，销售量将相应减少2 000件，要使销售的总收入不低于原收入， 该商品每件定价最多为多少元？(2)为了抓住此次契机，扩大该商品的影响力，提高年销售量，公司决定立即对该商品进行全面技术革新和营销策略改革，并提高定价到元.公司拟投入( - 600)万元作为技改费用，投入50万元作为固定宣传费用，投入万元作为浮动宣传费用.试问：当该商品改革后的销售量至少应达到多少万件时，才可能使改革后的销售收入不低于原收入与总投入之和？并求出此时商品的每件定价.【答案】(1)要使销售的总收入不低于原收入，每件定价最多为40元(2)当该商品改革后的销售量至少达到10.2万件时，才可能使改革后的销售收入不低于原收入与总投入之和，此时该商品的每件定价为30元 【分析】（1）设每件定价为元，则提高价格后的销售量为，根据销售的总收入不低于原收入，建立不等式，解不等式可得每件最高定价；（2）依题意，时，不等式有解，等价于时，有解，利用基本不等式，可以求得结论．【详解】(1)解：设每件定价为t元，依题意得，整理得 ，解得.所以要使销售的总收入不低于原收入，每件定价最多为40元.(2)解：依题意，时，不等式有解 等价于时，有解（当且仅当时，等号成立）．此时该商品的每件定价为30元当该商品明年的销售量至少应达到10.2万件时，才可能使明年的销售收入不低于原收入与总投入之和，此时该商品的每件定价为30元．