2022-2023学年陕西省咸阳市高新一中高一上学期期中数学试题（A卷）（解析版）

这是一份2022-2023学年陕西省咸阳市高新一中高一上学期期中数学试题（A卷）（解析版），共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．已知集合，则M的非空子集的个数是（ ）
A．7B．8C．15D．16
【答案】C
【分析】解分式不等式求集合M，并确定元素个数，根据元素个数与集合子集的数量关系求M的非空子集的个数.
【详解】由题设，，即，可得，
∴共有4个元素，故M的非空子集的个数.
故选：C
2．已知集合.若，则实数的取值范围是（ ）
A．B．C．D．
【答案】A
【分析】分，和三种情况讨论求解.
【详解】解：，
①当时，即时，，则；
②当时，即或时，
当时，，则，所以不合题意，
当时，，则；
③当时，即或时，设方程的两个根分别为，
则
当时，则，所以至少有一个负根，不合题意，
当时，则，所以的两根均为正数，符合题意.
综上所述，实数a的取值范围为.
故选：A
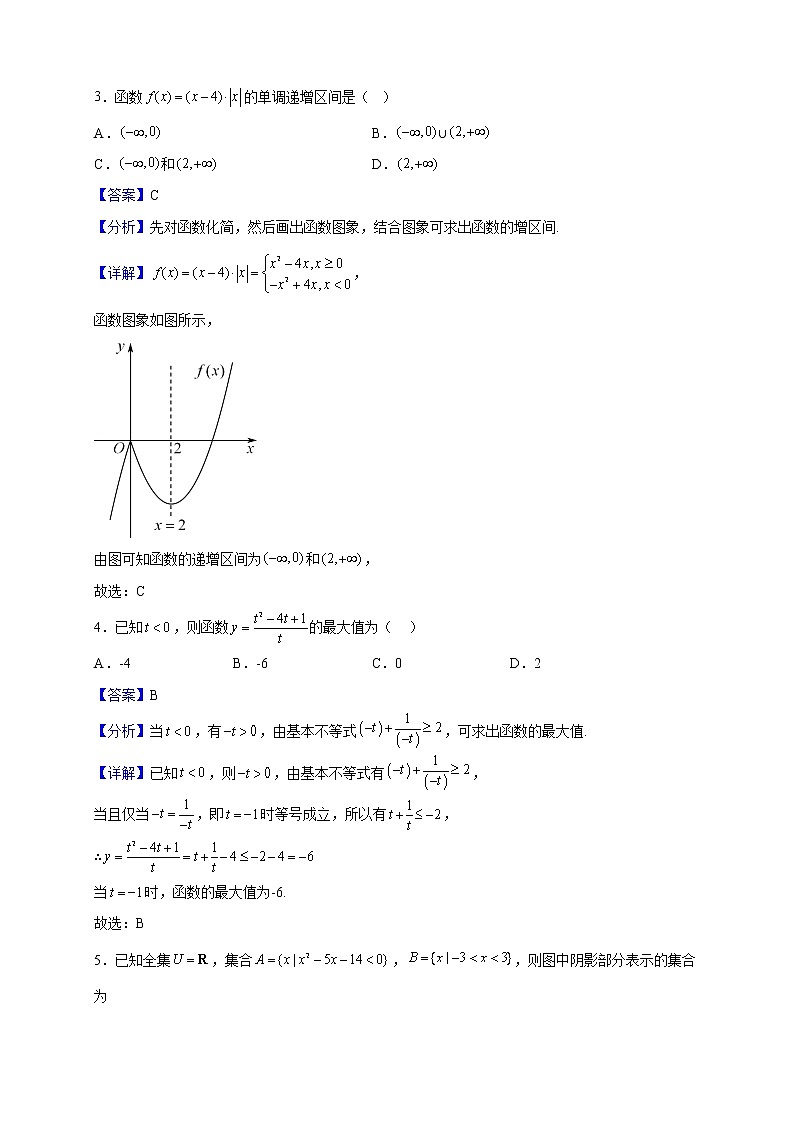
3．函数的单调递增区间是（ ）
A．B．∪
C．和D．
【答案】C
【分析】先对函数化简，然后画出函数图象，结合图象可求出函数的增区间.
【详解】，
函数图象如图所示，
由图可知函数的递增区间为和，
故选：C
4．已知，则函数的最大值为（ ）
A．-4B．-6C．0D．2
【答案】B
【分析】当，有，由基本不等式，可求出函数的最大值.
【详解】已知，则，由基本不等式有，
当且仅当，即时等号成立，所以有，
∴
当时，函数的最大值为-6.
故选：B
5．已知全集，集合，，则图中阴影部分表示的集合为
A．B．C．D．
【答案】D
【详解】分析：先求出A集合，然后由图中阴影可知在集合A中出去A,B的交集部分即可.
详解：由题得：
所以
故有题中阴影部分可知：阴影部分表示的集合为
故选D.
点睛：考查集合的交集和补集，对定义的理解是解题关键，属于基础题.
6．是成立的（ ）
A．充要条件B．充分不必要条件
C．必要不充分条件D．既不充分也不必要条件
【答案】B
【分析】根据不等式的性质，分别判断充分性和必要性.
【详解】充分性：由，得，故成立，即充分性成立.
必要性：由，得，当时，不等式也成立，即必要性不成立.
∴是成立的充分不必要条件.
故选：B
7．命题“”的否定形式是（ ）
A．B．
C．或 D．或
【答案】D
【分析】由特称命题的否定：存在改任意并否定原结论，即可得答案.
【详解】特称命题的否定是全称命题，原命题的否定形式为“或”.
故选：D
8．已知函数()，若函数 有三个零点，则a 的取值范围是( )
A． B．
C． D．
【答案】A
【分析】有三个零点转化为与的图象有三个交点，当时，有两个交点，只需当时的图象与的图象有1个交点，接下来分和，求出的值，进而确定的取值范围.
【详解】因为函数有三个零点，
所以的图象与的图象有三个交点.
因为，所以当时，由得，或，
所以当时，的图象与的图象有两个交点，
则当时的图象与的图象有1个交点.
令，得，所以符合题意;
令，得或(舍去)，所以符合题意.
综上，的取值范围是，
故选:A.
9．函数的零点所在的区间为（ ）
A．（0，1）B．（1，2）C．（2，3）D．（3，4）
【答案】A
【分析】分别求区间端点处的函数值，利用零点存在定理判断零点所在的区间.
【详解】函数是定义在R上的连续递增函数，
，，
由零点存在定理，函数零点所在的区间为（0，1）.
故选：A
10．定义在R上的函数满足，且当时，，则等于（ ）
A．2B．C．D．4
【答案】D
【分析】根据已知条件可得函数的周期为4，然后利用周期结合已知解析式可求得结果.
【详解】因为，
所以，
所以函数的周期为4，
因为当时，，
所以.
故选：D
11．已知奇函数f（x）的定义域为[-3，3]，且在区间[-3，0]上单调递增，则满足f（2-2m）+f（1-m2）>0的实数m的取值范围是（ ）
A．[-3，]B．[- ，2）
C．[- ，1）D．[-3，1）
【答案】C
【分析】利用函数的奇偶性与单调性并结合函数的定义域列出不等式组，解之即可求出结果.
【详解】∵f（x）是定义在[-3，3]上的奇函数，且在区间[-3，0]上单调递增，
所以在区间[-3，3]上单调递增，又因为，
也即，
所以，解得：，
故实数的取值范围为，
故选：.
12．已知是定义在上的偶函数，且在上单调递增，对于任意实数，（）恒成立，则的最小值是（ ）
A．B．C．D．
【答案】A
【分析】先结合偶函数的单调性去掉记号，然后分离参数，利用基本不等式处理恒成立问题即可.
【详解】是上的偶函数，则，于是可转化为，而在上单调递增，故，，两边同时除以可得：，于是，时，，时，，当，即取等号，故，于是，故，即的最小值是.
故选：A
二、填空题
13．设集合，，若，则实数对的取值集合是_____.
【答案】
【分析】根据集合相等的定义，两个集合中元素对应相等，结合元素的互异性分类讨论构造不同的方程组，即可得到结论
【详解】解： ，由元素的互异性可知集合B中的元素且，故且，
由，则集合A中只能是，此时在的条件下，有，
即或，解得或，实数对的取值集合是.
故答案为：
14．已知 且 ，则 的最小值为____.
【答案】9
【分析】由，得=1,使用不等式“1”的代换求解.
【详解】由，得=1，
则=，
当且仅当，即时取“=”.
故答案为：9.
15．已知函数，则满足的取值范围是____.
【答案】
【分析】根据解析式及对称性画出与的图象，数形结合判断不等式成立条件下x的范围.
【详解】由题意知，，即.
根据解析式，分别画出与的图象，如下图示，
由图象知，满足的x的取值范围是.
故答案为：
16．设奇函数在上是增函数，，若对所有的都成立，则实数t的取值范围是____．
【答案】或
【分析】根据题意，由函数的奇偶性与单调性分析可得在区间上，，据此分析：若对所有的都成立，必有恒成立，即恒成立，解即可得答案．
【详解】根据题意，函数在上是增函数，则在区间上，，
又由为奇函数，则，
若对所有的都成立，
必有恒成立，即恒成立，
解可得：或，
则t的取值范围为：或，
故答案为或．
【点睛】本题考查函数的奇偶性与单调性的综合应用，涉及函数的最值以及恒成立问题，属于综合题．
三、解答题
17．已知集合，．若“x∈A”是“x∈B”的充分条件，求实数m的取值范围．
【答案】
【分析】先求解集合A，然后利用x∈A”是“x∈B”的充分条件，得到A⊆B，进而比较端点值大小求解实数m的取值范围
【详解】，
因为，所以，
所以．
由x+m2≥1，得x≥1-m2，所以B={x|x≥1-m2}．
因为“x∈A”是“x∈B”的充分条件，
所以A⊆B，所以，解得：或，
故实数m的取值范围是．
18．设集合，．
(1)若，求实数a的取值范围；
(2)若，求实数a的取值范围．
【答案】(1)
(2)
【分析】（1）由可知，进而得到，将A中元素代入集合B中方程即可.
（2）由可知,分别讨论或或或四种情况a的取值情况，取并集即可.
【详解】（1）由可知
又因，可知
将代入，可得
将代入，可得或
将代入，可得
综上若，
（2）因，可知或或或
若，由(1)可知;
若，由(1)可知;
若,将代入，可得或
且，得，故不存在a使得集合;
若，则,得.
综上，
19．已知函数.
(1)求的值；
(2)若满足对任意、，都有成立，求实数的最小值.
【答案】(1)
(2)
【分析】（1）利用函数的解析式由内到外逐层计算可得出的值；
（2）分析可知函数在上单调递减，根据分段函数的单调性可得出关于实数的不等式组，即可解得实数的最小值.
【详解】（1）解：由题意可得，则.
（2）解：不妨设，由可得，
所以，函数在上单调递减，则，解得.
因此，实数的最小值为.
20．已知函数.
(1)判断并证明函数在的单调性.
(2)若时函数的最大值与最小值的差为，求的值.
【答案】(1)单调递增，证明见解析；
(2)2.
【分析】（1）根据单调性的定义，结合函数解析式，即可判断和证明；
（2）根据（1）中所求函数单调性，求得的最大值和最小值，结合题意，即可求得参数值.
【详解】（1）函数在上单调递增，证明如下：
任取，且，
因为，则，
因为，所以，，，
所以，即，
所以函数在上单调递增.
（2）由（1）知函数在上单调递增，
所以函数的最大值为，最小值为，
所以，即，解得.
21．小王大学毕业后，决定利用所学专业进行自主创业．经过市场调查，生产某小型电子产品需投入年固定成本为3万元，每生产x万件，需另投入流动成本为万元．在年产量不足8万件时，万元；在年产量不小于8万件时，万元，每件产品售价为5元．通过市场分析，小王生产的商品当年能全部售完．
(1)写出年利润万元关于年产量x万件的函数解析式．注：年利润=年销售收入-固定成本-流动成本
(2)年产量为多少万件时，小王在这一商品的生产中所获利润最大？最大利润是多少？
【答案】(1)
(2)年产量为10万件时，小王在这一商品的生产中所获利润最大，最大利润是15万元
【分析】（1）根据题意分和求出利润，得利润的分段函数；
（2）分别利用二次函数及均值不等式求最值，比较大小可得函数的最大值.
【详解】（1）因为每件产品售价为5元，则x（万件）商品销售收入为5x万元，依题意得：
当时，，
当时，，
∴．
（2）当时，，此时，当时，取得最大值9；
时，，
此时，当即时，取得最大值15；
∵，
∴年产量为10万件时，小王在这一商品的生产中所获利润最大，最大利润是15万元．
22．对于函数，若存在，使成立，则称为的不动点，已知函数．
（Ⅰ）当时，求的不动点；
（Ⅱ）若对任意实数，函数恒有两个相异的不动点，求的取值范围．
【答案】（Ⅰ）-1，3；（Ⅱ）
【详解】试题分析：（Ⅰ）解方程解得不动点；（Ⅱ）恒有两个相异实根，即判别式恒大于零，再根据二次函数图像知判别式小于零，解得的取值范围
试题解析：
（Ⅰ）当时，，由题意可知，得，
故当时，的不动点为-1，3.
（Ⅱ）因为恒有两个不动点，
所以，即恒有两个相异实根，
所以恒成立，于是设，所以恒成立，
所以，解得，故当．
恒有两个相异的不动点时，的取值范围是．