数学必修 第二册5.1 直线与平面垂直同步达标检测题

这是一份数学必修 第二册5.1 直线与平面垂直同步达标检测题，共27页。
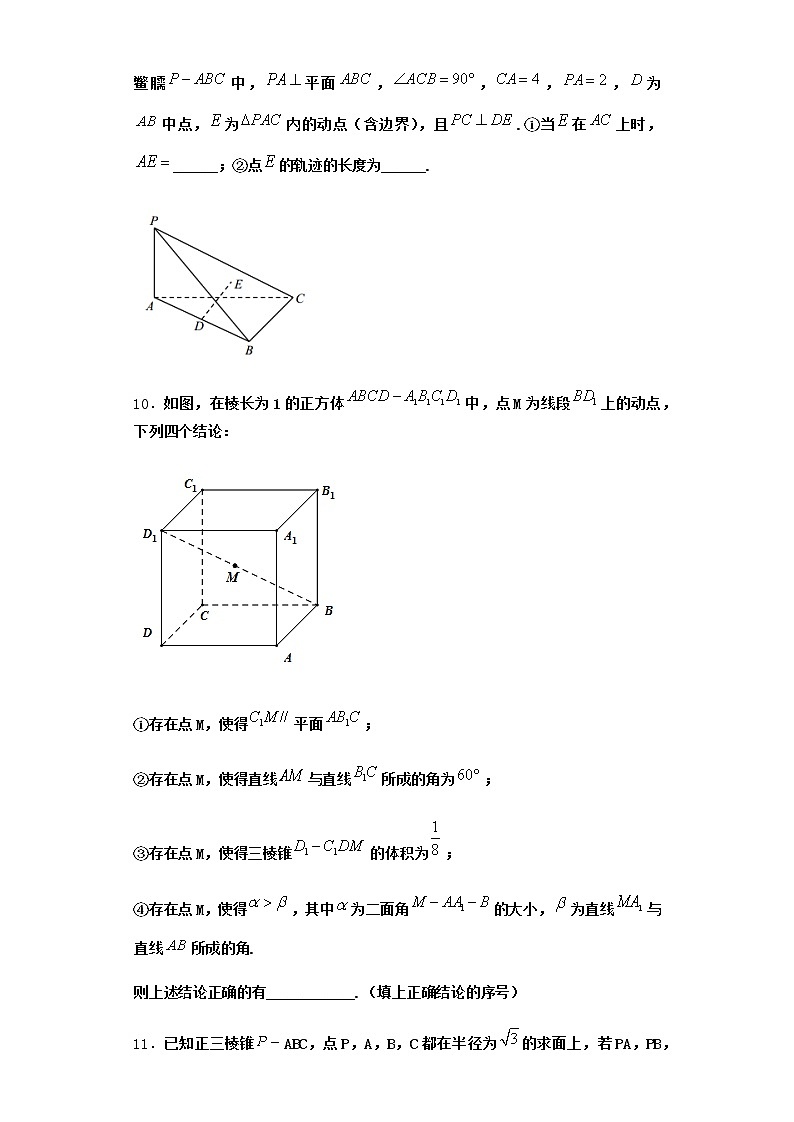
【特供】5.1 直线与平面垂直-2作业练习一．填空题1．三棱锥中，，且平面平面，则__________；若球与该三棱锥除以外的5条棱均相切，则球的半径为__________.2．在四棱锥中，平面，，点是矩形内（含边界）的动点，且，，直线与平面所成的角为.记点的轨迹长度为，则______；当三棱锥的体积最小时，三棱锥的外接球的表面积为______.3．已知正四面体的外接球与内切球上各有一个动点M．N，若线段的最小值为，则下列几个命题中，真命题的序号是________.①正四面体的体积与其外接球的体积的比为；②正四面体的内切球的表面积为；③正四面体的棱长为6；④线段的最大值为.4．正方体的棱长为2，点在棱上运动，过三点作正方体的截面，若为棱的中点，则截面面积为_________，若截面把正方体分成体积之比为的两部分，则=_______.5．边长为2的等边和直角所在半平面构成的二面角，当，时，线段的长度为______.6．在我国古代数学名著《九章算术》中，将四个面都为直角三角形的四面体称为鳖儒.如图，在鳖臑中，平面，其三视图是三个全等的等腰直角三角形，则异面直线与所成的角的余弦值为______.7．在三棱锥中，，，，则三棱锥的外接球的表面积为__________.8．如图，已知是平面的一条斜线，为斜足，，为垂足，为内的一条直线，，，则斜线和平面所成角是________.9．《九章算术》中，将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的鳖臑中，平面，，，，为中点，为内的动点（含边界），且.①当在上时，______；②点的轨迹的长度为______.10．如图，在棱长为1的正方体中，点M为线段上的动点，下列四个结论：①存在点M，使得平面；②存在点M，使得直线与直线所成的角为；③存在点M，使得三棱锥的体积为；④存在点M，使得，其中为二面角的大小，为直线与直线所成的角.则上述结论正确的有____________.（填上正确结论的序号）11．已知正三棱锥ABC，点P，A，B，C都在半径为的求面上，若PA，PB，PC两两互相垂直，则球心到截面ABC的距离为________．    
12．正方体的12条棱的中点和8个顶点共20个点中，任意两点连成一条直线，其中与直线垂直的直线共有________条.13．已知三棱锥的各顶点都在同一球面上，且平面，若该棱锥的体积为，，，，则此球的表面积=________．14．在三棱锥中，平面，，，，是上的一动点，且直线与平面所成角的最大值为，则________，三棱锥的外接球的表面积为________．15．已知P，A，B，C是球O的球面上的四个点，平面，则球O的表面积为__________．
参考答案与试题解析1．【答案】      【解析】设为的中点，利用面面垂直的性质定理以及线面垂直的性质得出，再由勾股定理得出，从而得出；设，分别为对应面的内心，分别过，作，的平行线，交于点，即为所求的球心，根据题意得出是正方形，得出内切圆的半径，即可得出球的半径.详解：如图，设为的中点，因为，所以，又因为平面平面，所以由面面垂直的性质定理得平面，所以因为，所以从而可得，.设，分别为对应面的内心，分别过，作，的平行线，交于点即为所求的球心，易知是正方形设内切圆的半径为，球的半径为，由图可知，而，所以.故答案为：；【点睛】本题主要考查了面面垂直性质的应用以及几何体的切接问题，属于中档题.2．【答案】      【解析】先根据已知条件判断出点的轨迹为圆弧，再求此时的，即可求出；判断三棱锥的体积最小时即点位于时，此时三棱锥的外接球球心为的中点，所以半径为的一半，从而可得外接球的表面积.详解：如图，因为平面，垂足为，则为直线与平面所成的角，所以.因为，所以，所以点位于底面矩形内的以点为圆心，为半径的圆上，记点的轨迹为圆弧.连接，则.因为，，所以，则弧的长度，所以.当点位于时，三棱锥的体积最小，又，∴三棱锥的外接球球心为的中点.因为，所以三棱锥的外接球的表面积.故答案为：；【点睛】本题考查了由线面垂直得到线面角，判断出动点轨迹，外接球的半径及表面积的计算，属于较难题.3．【答案】①②③④【解析】首先求出正四面体的外接球半径与内切球的半径，然后根据求出正四面体的棱长，然后逐一判断即可.详解：设正四面体的棱长为，则它的外接球与内切球的球心重合，作平面，垂足为，则为的重心，且则正四面体的高为，设正四面体的外接球半径为，内切球的半径为由图可知，，解得，.依题意可得，解得，故③正确；对于①，正四面的体积为：，外接球的体积为：，所以正四面体的体积与其外接球的体积的比为，故①正确；对于②，内切球的表面积为：，故②正确；对于④，线段的最大值为：，故④正确；故答案为：①②③④【点睛】本题考查了多面体的外接球．内切球问题．棱锥的体积公式．球的体积公式以及表面积公式，考查了考生的空间想象能力与运算求解能力，属于中档题.4．【答案】      【解析】（1）首先作出截面，再求截面的面积；（2）取上的点，，连接，由题意可知，利用体积公式求即可.详解：（1）取的中点，连接，，，而，四点共面，且四边形是等腰梯形，如下图，过作，垂足为，，，,，，；（2）设，取上的点，，连接，由（1）知四点共面，由图形可知，即 ，解得：，或（舍去），因此故答案为： ；【点睛】本题考查截面面积和几何体的体积，意在考查空间想象能力和计算能力，属于中档题型，本题的关键作出过点的平面.5．【答案】.【解析】作于,面于,再根据构造出的三角形求解对应的边长进行求解即可.【详解】作于,面于,连接易得为等边和直角所在半平面构成的二面角.又,,故,...画出底面分析可知..故.故答案为：【点睛】本题主要考查了根据空间中的边角关系计算线段长度的问题,需要作出辅助线构造直角三角形进行求边长的运算.属于中档题.6．【答案】【解析】取，，，的中点，连接，根据三视图可设，在中，利用余弦定理即可求解.详解：取，，，的中点，连接，则，，即异面直线与所成的角为，根据题意，由三视图可知，设，则，且，在中，由余弦定理可得.故答案为：【点睛】本题考查了求异面直线所成的角．余弦定理，属于中档题.7．【答案】【解析】作出在面上射影，是的外心，由正弦定理计算出，则可得，外接球球心在直线上，计算出长，知在延长线上，利用勾股定理求得外接球半径，可得表面积．详解：如图，平面，垂足为，因为，所以是外心，延长交于，因为，则是中点且，由已知，，由正弦定理，解得，由平面，得，所以，因为，所以三棱锥的外接球球心在上，且在延长线上，如图，设外接球半径为，，由得，解得，所以外接球表面积为．故答案为：20π.【点睛】本题考查求棱锥外接球表面积，解题关键是找出外接球球心，求出外接球半径，解题时利用性质“三棱锥外接球的球心一定在过各面外心且与此面垂直的直线上”易找到球心位置．8．【答案】【解析】在平面内作，垂足为点，连接，设，计算出．，可求得的值，由此可求得斜线和平面所成的角的大小.详解：如下图所示，在平面内作，垂足为点，连接， 设，在中，，则，，，，又，，平面，平面，，，，，所以，直线与平面所成的角为，在中，，，因此，直线与平面所成的角为.故答案为：.【点睛】本题考查直线与平面所成角的计算，考查计算能力，属于中等题.9．【答案】2      【解析】(1)根据与鳖臑的性质证明平面再求解即可.(2)根据(1)中的计算可知垂直于所在的平面,再得出垂直于在平面内的轨迹再计算长度即可.详解：(1)当在上时,因为平面,故,又,故平面.故.又,为中点,故所以为中点.故.(2)取中点则由(1)有平面,故,又,设平面则有平面.故点的轨迹为.又此时,,故.所以.故答案为：(1). 2    (2). 【点睛】本题主要考查了根据线面垂直与线面垂直的性质求解立体几何中的轨迹问题,需要根据垂直关系求解对应的线段长度.属于中档题.10．【答案】①③【解析】①由平面平面可判断; ②由直线平面可判断; ③由点M到平面的距离，可判断；④过作,由平面,所以平面，进一步作出的平面角，即，又由，直线与直线所成的角为，根据最小角定理可判断，得出答案.详解：对于①.  连接,由,平面,平面,所以平面.同理平面且所以平面平面,显然直线与平面相交，设交点为M.则平面，所以平面，所以①正确.对于②. 连接,则,且所以直线平面,而平面,所以,所以②不正确.对于③. 由点M为线段上的动点，所以点M到平面的距离..所以存在点M，使得三棱锥的体积为，故③正确.对于④. 过作,由平面,所以平面过作交于点，则，连接.所以,又，且,所以平面.所以，所以为二面角的平面角，即由，所以直线与直线所成的角与直线与直线所成的角相等.所以直线与直线所成的角为.由平面，平面,所以平面平面,且平面平面所以直线在平面上的射影为.所以直线与平面所成的角为，即为.直线与平面内的直线（，）所成角中（由最小角定理可得），线面角最小.所以小于等于直线与直线所成的角.所以④不正确.故答案为：①③下面补证最小角定理：平面外的一条斜线和它在平面内的射影所成的锐角，是这条斜线和平面内经过斜足的直线所成的一切角中最小的角平面斜交的直线与它在该平面内的射影的夹角不大于直线与平面内其他直线的夹角．直线与平面斜交，斜足为，平面，，由平面，，可证明平面，则．则，，，所以，即，故，．【点睛】本题考查线面平行的证明，体积的求解，二面角和异面直线成角的大小的比较，考查存在问题的探索，考查最小角定理，属于难题.11．【答案】【解析】正三棱锥P-ABC可看作由正方体PADC-BEFG截得，如图所示，PF为三棱锥P-ABC的外接球的直径，且,设正方体棱长为a，则，由，得，所以，因为球心到平面ABC的距离为.考点定位：本题考查三棱锥的体积与球的几何性质，意在考查考生作图的能力和空间想象能力 12．【答案】【解析】作出图形，找出与直线垂直的平面，利用组合计数原理和分类加法计数原理计算出每个截面顶点两两连线的条数，即可得出结果.【详解】如下图所示：连接，四边形为正方形，，平面，平面，，，平面，平面，，同理，，所以，平面，易知与平面平行的平面有：平面．平面．平面．平面，截面．．．均为三角形，此时与垂直的直线有条；截面为六边形，此时与垂直的直线有条.综上所述，与垂直的直线有条.故答案为：.【点睛】本题考查满足条件的直线条数的求法，考查组合计数原理与分类加法计数原理的应用，是中档题，解题时要注意空间思维能力的培养．13．【答案】【解析】先根据锥体体积公式求,再解三角形得三角形为直角三角形，确定其外心为AB中点，进而确定三棱锥外接球球心位置，最后解得外接球半径，求得球的表面积.【详解】因为棱锥的体积为，平面，所以，，，，，即三角形为直角三角形，其外心为AB中点，从而三棱锥的外接球球心满足平面，即外接球半径,因此外接球的表面积为，故答案为：【点睛】本题考查三棱锥外接球的表面积，考查空间想象能力以及分析求解能力，属中档题.14．【答案】6      【解析】（1）设直线与平面所成的角为，先求出的最小值为，的最小值是，即点到的距离为，再利用余弦定理求出的值；（2）取的外接圆的圆心为，则圆的半径，连接，作于点，即得，即得解.详解：设直线与平面所成的角为，三棱锥外接球的球心为，半径为，如图所示，则，所以，则的最小值为，的最小值是，即点到的距离为，所以．因为，所以，所以，所以，所以．取的外接圆的圆心为，则圆的半径．连接，作于点，则点为的中点，所以，故三棱锥的外接球的表面积．故答案为：6；.【点睛】本题主要考查空间角的计算，考查几何体外接球的问题的处理，考查球的表面积的计算，意在考查学生对这些知识的理解掌握水平.15．【答案】【解析】画出图象，利用补形的方法求得球的半径，进而求得球的表面积.详解：由于平面，所以，而，故可将补形为长方体，如图所示，长方体的外接球，也即三棱锥的外接球，也即球.由于，设，则，所以长方体的对角线长为.设球的半径为，则，所以球的表面积为.故答案为：【点睛】本小题主要考查几何体外接球表面积的计算，属于基础题.