高中数学北师大版 (2019)必修 第二册5.2 平面与平面垂直习题

这是一份高中数学北师大版 (2019)必修 第二册5.2 平面与平面垂直习题，共22页。
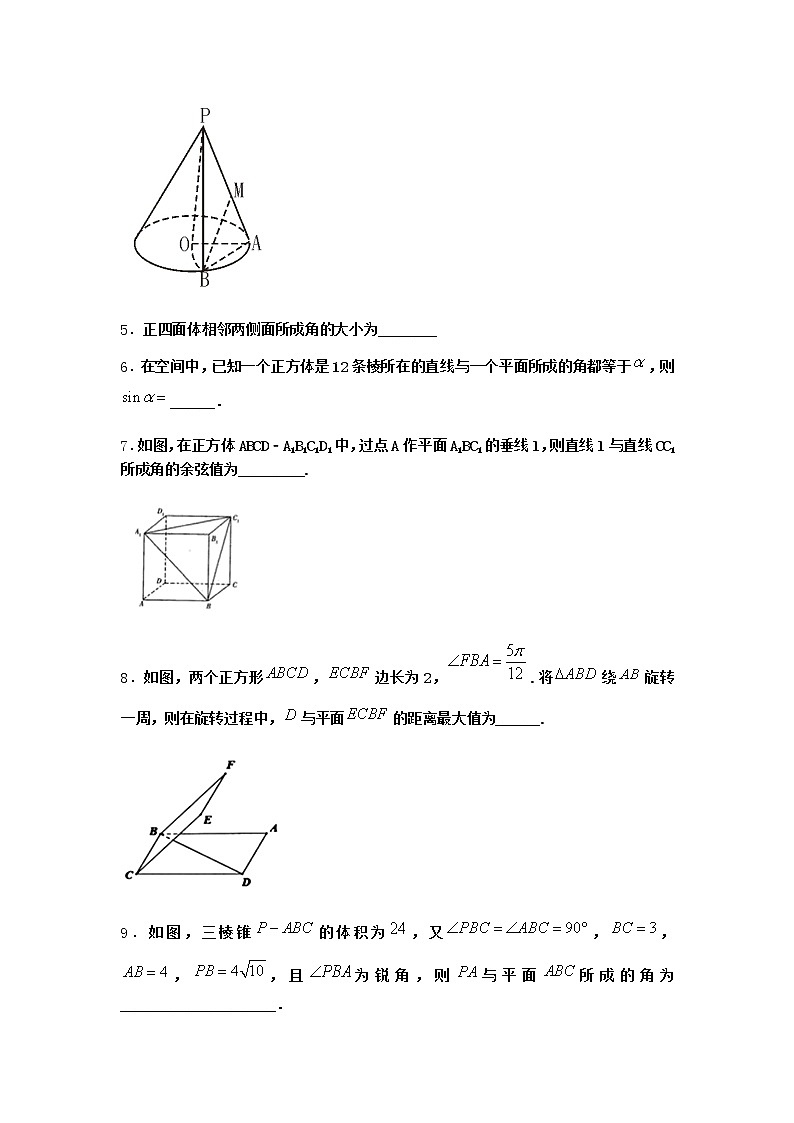
【精选】5.2 平面与平面垂直-2课时练习一．填空题1．在正三棱锥中，D，E分别是AB，BC的中点，有下列三个论断：；平面PDE；  平面其中正确的个数是______．2．正方形的边长为2，沿着对角线把平面向上折起得到三棱锥，则三棱锥的体积的最大值为______________．3．如图，在四棱锥中，平面，，，，，分别为棱上一点，若与平面所成角的正切值为2，则的最小值为________.4．如图圆锥高为2，侧面积为，为顶点，为底面中心，，在底面圆周上，为中点，，则到面的距离为______.5．正四面体相邻两侧面所成角的大小为________6．在空间中，已知一个正方体是12条棱所在的直线与一个平面所成的角都等于，则______．7．如图，在正方体ABCD﹣A1B1C1D1中，过点A作平面A1BC1的垂线l，则直线l与直线CC1所成角的余弦值为_________.8．如图，两个正方形，边长为2，.将绕旋转一周，则在旋转过程中，与平面的距离最大值为______.9．如图，三棱锥的体积为，又，，，，且为锐角，则与平面所成的角为_____________________．10．在三角形ABC中，，D是垂足，则推广到空间，三棱锥中，面面，O为垂足，且O在三角形BCD内，则类似的结论为___________11．已知四棱锥的底面是边长为的正方形，其外接球的表面积为，是等边三角形，平面平面，则______ .12．如图，在三棱柱中，底面，，，，，则直线与所成角的大小为_____________.13．如图，在多面体ABCDEF中，平面平面ABCD，是正三角形，四边形ABCD是正方形，，，则多面体ABCDEF的体积为________.14．如图，在三棱锥O﹣ABC中，三条棱OA．OB．OC两两互相垂直，且OA＝OB＝OC，M是AB边的中点，则OM与平面ABC所成的角的余弦值_____．15．如图，在三棱锥中，若底面是正三角形，侧棱长，．分别为棱．的中点，并且，则异面直线与所成角为______；三棱锥的外接球的体积为______．
参考答案与试题解析1．【答案】2【解析】利用直线与平面平行的判定，以及直线与平面垂直的判定，直线的平行等判断．【详解】根据正三棱锥的性质可知对棱互相垂直，故正确；，面PDE，面PDE，平面PDE，故正确；若平面PDE，则，因为，所以 ,而正三棱锥中AC与AB不垂直， 故不正确．故答案为：2.【点睛】主要考查了直线与平面平行的判定，以及直线与平面垂直的判定考查的知识点比较多，属于基础题．2．【答案】【解析】根据三棱锥的体积公式可知，当底面积一定，高最大时，三棱锥的体积最大，所以折起后，当面面时，三棱锥的体积最大，即可求出．【详解】如图所示，当面面时，此时点A到面的距离最大，最大距离为三棱锥的体积最大为．故答案为：．【点睛】本题主要考查几何图形折叠形成的三棱锥体积的求法，意在考查学生的的直观想象能力和数学运算能力，属于基础题．3．【答案】【解析】先找出与平面所成角，再利用正切值为2，证得E为PC的中点.根据所给各边的长度，求出的斜弦值，再将翻折至与平面PAB共面，利用余弦定理求出，即为的最小值.【详解】取CD的中点H，连接BH，EH.依题意可得，.因为平面ABCD，所以，从而平面ABCD，所以BE与平面PCD所成角为，且，则，则E为PC的中点.    在中，.因为，，，所以，所以.将翻折至与平面PAB共面，如图所示，则图中，当F为AE与PB的交点时，取得最小值，此时，.故答案为：.【点睛】本题考查空间中线面垂直．线面角．余弦定理等知识的交会，考查空间相象能力和运算求解能力，将空间中线段和的最值问题，转化成平面问题，对转化与化归思想的考查要求较高，属于难题.4．【答案】【解析】先利用侧面积计算，再利用体积法得到，代入数据计算得到答案.【详解】如图所示：为中点，连接圆锥高为2，侧面积为即为中点，为中点，，故又，所以平面，故故为等边三角形.在中：，边上的高故答案为【点睛】本题考查了点到平面的距离，利用体积法可以简化运算，是解题的关键，意在考查学生的空间想象能力和计算能力.5．【答案】【解析】转化为侧面与底面所成角,取底面中心,连,延长交与,连,则可得为二面角的平面角,然后在直角三角形中计算可得.【详解】如图:因为正四面体的相邻两个侧面所成的角和侧面与底面所成的角相等,所以只需求侧面与底面所成角的大小,设正四面体的棱长为1,底面中心为,连,则平面,,连,并延长交于,则,连,则,且为的中点,所以就是侧面与底面所成二面角的平面角,因为,所以,所以在直角三角形中,所以.故答案为:.【点睛】本题考查了二面角的求法,解题关键是利用三垂线定理作出平面角,属于基础题.6．【答案】【解析】画出几何图形,可知面与12条棱所在的直线与一个平面所成的角都等于,在可求得.【详解】画出几何图形,可知面与12条棱所在的直线与一个平面所成的角都等于 正方体 面, 与面所成的角为不妨设正方体棱长为,故在中由勾股定理可得: 故答案为:.【点睛】本题考查了线面角求法,根据体积画出几何图形,掌握正方体结构特征是解本题的关键.属于基础题.7．【答案】【解析】连结DB1，则DB1⊥平面A1BC1，从而l∥DB1，直线l与直线CC1所成角为∠D1DB，由此能求出结果．【详解】如图，连结DB1，则DB1⊥平面A1BC1，∴l∥DB1，直线l与直线CC1所成角为，连结B1D1，在Rt△D1DB1中，设DD1＝a，则DB1，∴cos∠D1DB1．故答案为：．【点睛】本题考查异面直线所成角的余弦值的求法，考查空间中线线．线面．面面间的位置关系等基础知识，考查运算求解能力，是中档题．8．【答案】【解析】绕旋转一周得到的几何体是圆锥，点的轨迹是圆.过作平面平面，交平面于.的轨迹在平面内.画出图像，根据图像判断出圆的下顶点距离平面的距离最大，解三角形求得这个距离的最大值.【详解】绕旋转一周得到的几何体是圆锥，故点的轨迹是圆.过作平面平面，交平面于.的轨迹在平面内.画出图像如下图所示，根据图像作法可知，当位于圆心的正下方点位置时，到平面 的距离最大.在平面内，过作，交于.在中，,.所以①.其中，，所以①可化为.故答案为：【点睛】本小题主要考查旋转体的概念，考查空间点到面的距离的最大值的求法，考查空间想象能力和运算能力，属于中档题.9．【答案】.【解析】首先由线面垂直的判定定理得到平面，由线面垂直的性质得到，由计算出，再根据同角三角函数的基本关系得到，在中，由余弦定理求出的值，即可得到，从而得到平面，即可得解.【详解】解：因，即，，又平面，平面，所以平面，又，，，由勾股定理可得，，由三棱锥的体，解得，又为锐角，所以，在中，由余弦定理得，即，则，故，由平面，平面，，平面，平面，，故平面，故与平面所成的角为．故答案为：【点睛】本题考查线面垂直的判定及性质定理的应用，锥体的体积计算，属于中档题.10．【答案】【解析】这是一个类比推理的题，在由平面图形到空间图形的类比推理中，一般是由点的性质类比推理到线的性质，由线的性质类比推理到面的性质，由已知在平面几何中在△ABC中，AB⊥AC，点D是点A在BC边上的射影，则，我们可以类比这一性质，推理出若在三棱锥A？BCD中，BA⊥平面ACD，点O是点A在平面BCD内的射影，即可得到答案【详解】解：由已知在平面几何中，若三角形ABC中，，D是垂足，则，我们可以类比这一性质，推理出：若三棱锥中，面面，O为垂足，则。证明：如图，连接DO并延长，交BC与点E，连接AE，BO，CO，面，则，又面，则，所以在三角形中，，是垂足，则，，，故答案为：.【点睛】类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．11．【答案】【解析】利用外接球的表面积，求出四棱锥的外接球半径，进而利用勾股定理求解；【详解】解：根据题意，画出示意图如图所示，  为四棱锥的外接球的球心，为与交点，过作交与点，过作交与点，则，设，∵ 外接球的表面积是，得，在中，，在中，，联立以上两式解得，故答案为：．【点睛】考查四棱锥外接球的理解，勾股定理的应用，正确画出示意图是解决本题的关键．12．【答案】60°【解析】连接，根据平移找到直线与所成角，假设长度，计算长度，可得结果.【详解】连接.因为，，所以.易知//，所以就是直线与所成角.设，则，则是正三角形，则.故直线与所成角的大小为60°.故答案为：60°【点睛】本题考查异面直线所成的角，这种题型，有以下做法：① 向量法②平移或者作辅助线，找到这个角，根据特点或结合三角函数以及余弦定理求值，属基础题.13．【答案】【解析】如图所示，分别过作交于，作交于，于是将多面体ABCDEF分为一个棱柱和一个棱锥，分别求出其体积，即可求出．【详解】如图所示，分别过作交于，作交于，连接．因为平面平面ABCD，是边长为2的正三角形，所以到平面ABCD的距离为，且，故．故答案为：．【点睛】本题主要考查简单几何体的体积求法，涉及棱锥和棱柱的体积公式应用，意在考查学生的转化能力和直观想象能力，属于中档题．14．【答案】【解析】根据线面垂直的判定定理，根据三棱锥的体积公式，利用等积性，最后根据线面角的定义，求出OM与平面ABC所成的角的余弦值【详解】∵OA，OB，OC两两垂直，∴OA⊥平面OBC，设OA＝OB＝OC＝1，则AB＝BC＝AC，∴S△ABC．设O到平面ABC的距离为h，∵VO﹣ABC＝VA﹣OBC，∴，解得h，又OM，∴OM与平面ABC所成的角的正弦值为，∴OM与平面ABC所成的角的余弦值为．【点睛】本题考查了线面角，考查了等积性的应用，考查了数学运算能力.15．【答案】      【解析】根据题意得出三棱锥是正三棱锥，易证出平面，再根据，可得，从而得出异面直线与所成角；判断出三棱锥是正方体的一部分，从而得出球的直径，即可得出球的体积.【详解】由三棱锥中，若底面是正三角形，侧棱长知，三棱锥是正三棱锥，则点在底面中的投影为底面的中心，为中点如图，因此,所以平面,平面,,又．分别为棱．的中点，则,因此，异面直线与所成角为；,平面,又，则平面,又三棱锥是正三棱锥，因此三棱锥可以看成正方体的一部分且为正方体的四个顶点，故球的直径为，则球的体积为.故答案为：；.【点睛】本题主要考查的是异面直线所成角，线面垂直的判定定理，以及球的体积，考查学生的理解能力，是中档题.