高中数学北师大版 (2019)必修 第二册4.3 诱导公式与对称综合训练题

这是一份高中数学北师大版 (2019)必修 第二册4.3 诱导公式与对称综合训练题，共13页。试卷主要包含了已知，则_________.等内容，欢迎下载使用。
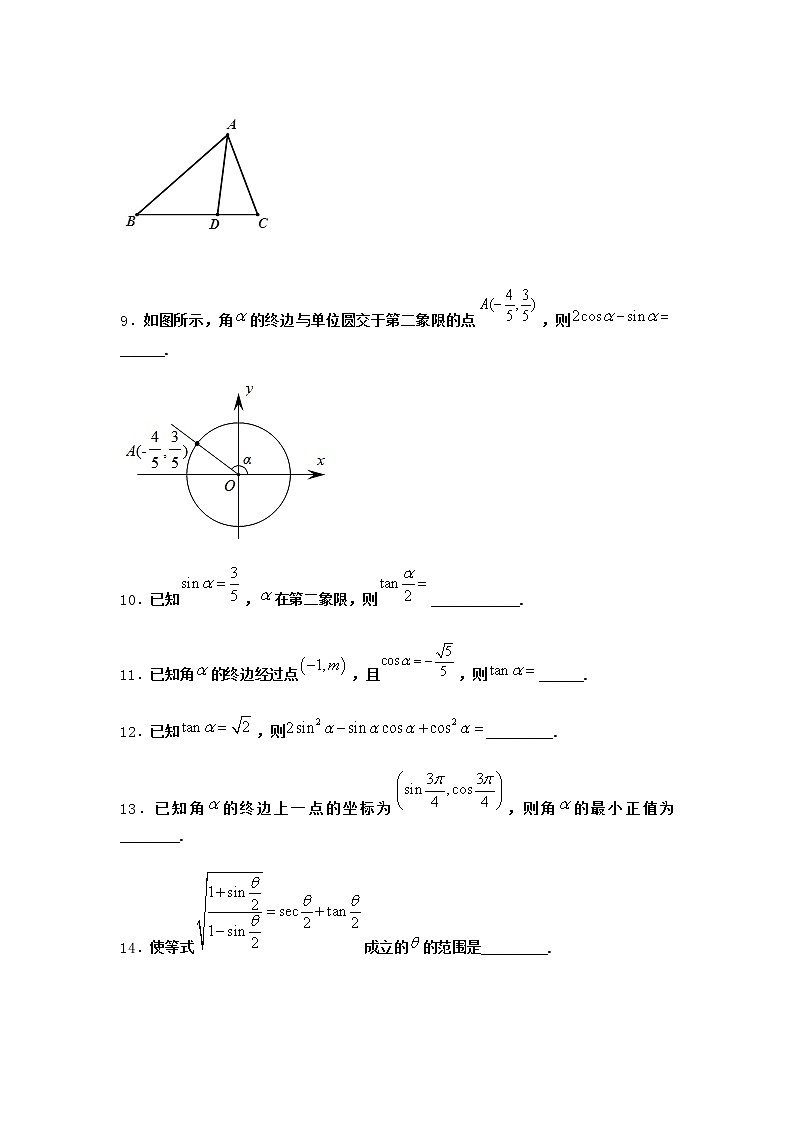
【精挑】4.3 诱导公式与对称-1优选练习一．填空题1．若角α的终边上一点的坐标为(1，－1)，则cos α＝________.2．已知角终边上有一点，则____________.3．已知，则_________.4．平面直角坐标系中，角的顶点与原点重合，始边与轴的正半轴重合，若其终边经过点，则________.5．以为始边作角，将的终边按照某种规律逆时针旋转得角，接下来按照同样的规律进行旋转，，依此类推，的终边旋转得角，已知，，．则_______________（用含的代数式表示）．6．函数的定义域是________.7．已知sinθ＋cosθ＝，θ∈(0，π)，则tanθ＝________.8．如图，在中，D为边上的一点，若，，，，则________，________.9．如图所示，角的终边与单位圆交于第二象限的点，则______.10．已知，在第二象限，则____________.11．已知角的终边经过点，且，则______.12．已知，则_________.13．已知角的终边上一点的坐标为，则角的最小正值为________.14．使等式成立的的范围是_________.15．已知，且，则________.
参考答案与试题解析1．【答案】【解析】根据的定义，即可代值求得结果.详解：因为的终边过点，故可得故答案为：.【点睛】本题考查利用角度终边上一点求三角函数值，属基础题.2．【答案】【解析】根据三角函数的定义得到，然后根据诱导公式和商数关系将齐次式化为的形式后求解即可得到结果．详解：∵角终边上有一点，∴．∴．故答案为．【点睛】（1）同角三角函数的基本关系反映了同一个角的不同三角函数之间的必然联系，它为三角函数的化简．求值．证明等提供了重要的方法．（2）在三角函数的化简求值问题中，关于的齐次式，往往化为关于的式子后再求解．3．【答案】【解析】利用诱导公式可求得的值，再利用同角三角函数的基本关系可求得的值，再结合诱导公式可求得所求代数式的值.详解：，由诱导公式可得，由同角三角函数的基本关系可得，解得，因此，.故答案为：.【点睛】本题考查利用诱导公式和同角三角函数的基本关系求值，考查计算能力，属于基础题.4．【答案】【解析】根据任意角的三角函数的定义计算.详解：因为角的终边经过点，所以.故答案为：【点睛】本题考查任意角的三角函数，属于基础题.5．【答案】【解析】由可得，代入化简可得结果.详解：，即，可得，所以，.故答案为：.【点睛】本题考查三角函数式的化简，考查切化弦思想的应用，考查计算能力，属于基础题.6．【答案】【解析】要使得函数有意义，则，然后解出即可.详解：要使得函数有意义则，所以即函数的定义域是故答案为：【点睛】本题考查的是三角函数在各个象限的符号，较简单.7．【答案】－【解析】根据1 =sin2θ＋cos2θ以及条件解方程组可得sinθ，cosθ，再根据同角三角函数关系得结果.详解：解方程组得或 (舍)．故tanθ＝－.【点睛】本题考查同角三角函数关系，考查基本求解能力.8．【答案】    2  【解析】由题意结合同角三角函数的平方关系可得．，再由差角的正弦公式即可得；再利用三角形面积公式结合等面积法即可得；即可得解.详解：，，，，，，；又，，的面积，，.故答案为：；.【点睛】本题考查了同角三角函数的平方关系．差角正弦公式的应用，考查了三角形面积公式及等面积法的应用，属于中档题.9．【答案】【解析】根据三角函数的定义可求的值，从而可求的值.详解：因为角的终边与单位圆交于第二象限的点，故，故.故答案为：.【点睛】本题考查三角函数的定义，一般地，设终边上异于原点的点为，则，解题中注意公式的正确应用.10．【答案】3【解析】由题意：，解得：或，又在第二象限，故．11．【答案】【解析】根据三角函数的定义，由，求得或，再分类讨论求解.【详解】解得或当时，-2当时，2综上：故答案为：【点睛】本题主要考查了三角函数的定义及其应用，还考查了分类讨论的思想方法，属于基础题.12．【答案】【解析】利用同角的三角函数的基本关系式可把化为，从而可求前者的值.详解：因为，故，故答案为：.【点睛】本题考查同角的三角函数的基本关系式，一般地，对于给值求值的问题，需结合给定的代数式的特征进行合理变形，如二次式可以利用平方关系转化为齐次式，再利用商数关系转化为关于的代数式.13．【答案】【解析】由得，然后可得详解：∵角的终边上一点坐标为，即，故点M在四象限，且，则角的最小正值为.故答案为：【点睛】本题考查的是特殊角的三角函数及三角函数的定义，较简单.14．【答案】【解析】等式左边分子分母同时乘以进行化简，等式右边利用割化弦，切化弦化简，利用左等于右，求出结果.详解：左边，右边，，.【点睛】本题考查同角三角函数的关系在化简证明中的应用，考查等式成立求角的取值范围问题，属于中档题.15．【答案】【解析】将变形为，利用平方关系并解方程得出或，结合商数关系进行讨论，即可得出答案.详解：由题意可知，则即整理得，解得或当时，，此时，则满足题意当时，，此时，不满足题意综上，故答案为：【点睛】本题主要考查了利用同角三角函数的基本关系求三角函数值，属于中档题.