

高中数学北师大版 (2019)必修 第二册4.3 诱导公式与对称课时训练
展开【优质】4.3 诱导公式与对称-2优选练习
一.填空题
1.若是三角形的内角,且,则的值为__________.
2.已知,则_________.
3.若,则______.
4.已知,则的值是______.
5.等腰三角形顶角的正弦为,则底角的余切为_________.
6.已知角的终边经过点,则________.
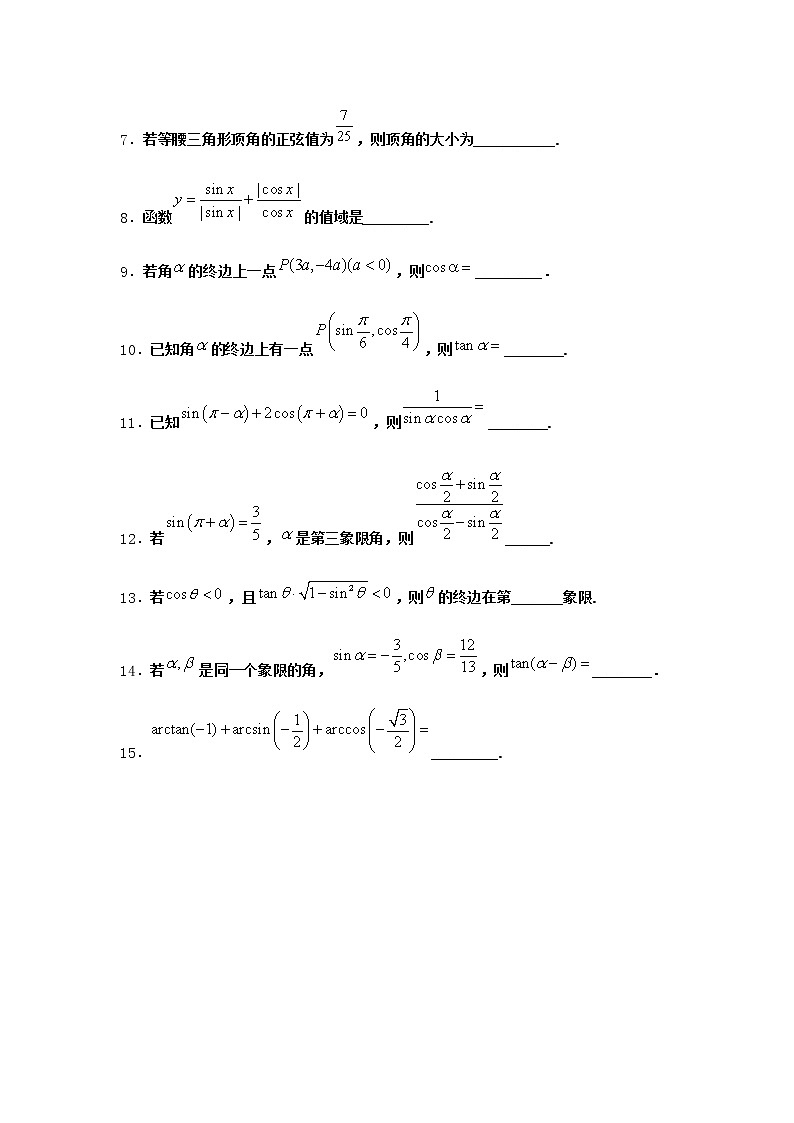
7.若等腰三角形顶角的正弦值为,则顶角的大小为___________.
8.函数的值域是_________.
9.若角的终边上一点,则_________.
10.已知角的终边上有一点,则________.
11.已知,则________.
12.若,是第三象限角,则______.
13.若,且,则的终边在第_______象限.
14.若是同一个象限的角,,则________.
15._________.
参考答案与试题解析
1.【答案】
【解析】根据题意,先得到,确定为钝角,得到,,再由,即可求出结果.
详解:因为,所以,因此,
又是三角形的内角,所以为钝角,
因此,,
所以.
故答案为:.
【点睛】
本题主要考查同角三角函数基本关系,属于基础题型.
2.【答案】
【解析】根据,得到,再将分子分母同除以,利用商数关系求解.
详解:因为,
所以,
所以.
故答案为:
【点睛】
本题主要考查同角三角函数基本关系式,还考查了运算求解的能力,属于中档题.
3.【答案】
【解析】将已知等式左右平方,结合同角三角函数平方关系可求得结果.
【详解】
故答案为:
【点睛】
本题考查利用同角三角函数关系求值的问题,属于基础题.
4.【答案】1
【解析】首先利用同角三角函数的基本关系求出,再利用平方关系将化成齐次式,最后代入求值.
【详解】
解:
故答案为:
【点睛】
本题考查同角三角函数的基本关系,属于基础题.
5.【答案】或2
【解析】设出顶角为,根据三角形的内角和定理表示出底角,由题意得到的值,由为三角形的内角,利用同角三角函数间的基本关系求出的值,表示出底角的余弦值和正弦值,即可求出底角的余切值.
详解:设顶角为,则底角为,
∴,
又为三角形的内角,∴,
当时,,
,
;
当时,,
,
;
故答案为:或2.
【点睛】
本题考查了同角三角函数间的基本关系,等腰三角形的性质,以及二倍角的余弦函数公式,熟练掌握基本关系是解本题的关键,属于中档题.
6.【答案】
【解析】直接利用三角函数的坐标定义求解.
【详解】
由题得.
故答案为:
【点睛】
本题主要考查三角函数的坐标定义,意在考查学生对该知识的理解掌握水平,属于基础题.
7.【答案】或
【解析】由角的正弦值,利用反三角即可直接表示出角的大小v
详解:解:等腰三角形顶角的正弦值为,
当等腰三角形的顶角是锐角时,顶角的大小为;
当等腰三角形的顶角是钝角时,顶角的大小为;
综合得顶角的大小为或.
故答案为:或.
【点睛】
本题考查利用反三角函数表示角,是基础题.
8.【答案】
【解析】分别讨论在第一象限,第二象限,第三象限,第四象限四种情况,计算得到答案.
详解:根据题意知:,,
当在第一象限时,;
当在第二象限时,;
当在第三象限时,;
当在第四象限时,;
综上所述:值域为.
故答案为:.
【点睛】
本题考查了三角函数的值域,意在考查学生的计算能力和分类讨论能力.
9.【答案】
【解析】由题意可得,,.利用已知条件,得到,利用任意角的三角函数的定义得到.
详解:解:由题意可得,,,
因为,
所以,
故答案为:.
【点睛】
本题考查任意角的三角函数的定义,两点间的距离公式的应用,注意,不是,此处是个易错点.
10.【答案】
【解析】先求出点的坐标,再利用正切函数的定义,求正切值.
【详解】
因为,
根据正切函数的定义:
故答案为:
【点睛】
本题考查三角函数的定义,涉及正切的定义,属三角定义基础题.
11.【答案】
【解析】利用诱导公式化简等式,可求出的值,将所求分式变形为,在所得分式的分子和分母中同时除以,将所求分式转化为只含的代数式,代值计算即可.
【详解】
,,,
因此,.
故答案为:.
【点睛】
本题考查利用诱导公式和弦化切思想求值,解题的关键就是求出的值,考查计算能力,属于基础题.
12.【答案】
【解析】利用平方关系和二倍角公式化简为,再利用,得到代入求解.
详解:因为,
又,
,
为第三象限角,
.
故答案为:
【点睛】
本题主要考查同角三角函数基本关系式,诱导公式以及二倍角公式,还考查了运算求解的能力,属于中档题.
13.【答案】二
【解析】利用平方关系可将已知化为,再结合以及商的关系即可得到答案.
详解:因为,所以,
所以,,故的终边在第二象限.
故答案为:二
【点睛】
本题主要考查同角三角函数的基本关系的应用,涉及到三角函数值的符号判定,考查学生的基本计算能力,是一道容易题.
14.【答案】
【解析】利用同角三角函数的基本关系求得cosα和sinβ的值,可得tanα.tanβ的值,利用利用两角差的正切公式,求得tan(α﹣β)的值.
详解:若是同一个象限的角,,故为第四象限角,
∴cosα,tanα, sinβ,
∴tanβ,
则 tan(α﹣β)
故答案为:
【点睛】
本题主要考查同角三角函数的基本关系.两角差的正切公式的应用,准确计算是关键,属于基础题.
15.【答案】
【解析】直接利用反三角函数的定义求值,即可求得答案.
详解:
故答案为:.
【点睛】
本题主要考查反三角函数的求值问题,要注意反三角函数的值域,属于基础题.
北师大版 (2019)必修 第二册4.3 诱导公式与对称课后练习题: 这是一份北师大版 (2019)必修 第二册4.3 诱导公式与对称课后练习题,共12页。试卷主要包含了化简___________.,已知,且,则________., =_________;,若,则________.,已知,则__________,已知,则__________.等内容,欢迎下载使用。
高中数学北师大版 (2019)必修 第二册4.3 诱导公式与对称课堂检测: 这是一份高中数学北师大版 (2019)必修 第二册4.3 诱导公式与对称课堂检测,共11页。试卷主要包含了若,则__________.,已知,则______.,已知,则的值为_______.等内容,欢迎下载使用。
北师大版 (2019)必修 第二册4.3 诱导公式与对称当堂达标检测题: 这是一份北师大版 (2019)必修 第二册4.3 诱导公式与对称当堂达标检测题,共10页。试卷主要包含了若,则______.,定义在R上的奇函数满足, ,已知,则__________,若,则=__________等内容,欢迎下载使用。













