

高中数学北师大版 (2019)必修 第二册第二章 平面向量及其应用6 平面向量的应用6.1 余弦定理与正弦定理当堂达标检测题
展开【优编】6.1 余弦定理与正弦定理-1优选练习
一.填空题
1.已知直线l:mx+2y+6=0,向量(1-m,1)与l平行,则实数m=________.
2.,为平面向量,已知=(4,3),2+=(3,18),则,夹角的余弦值等于 .
3.在直角中,,, ,为斜边的中点,则 =____________.
4.已知向量,,且与的夹角为,若,则实数的取值范围是 .
5.在平行四边形中,若,,则___________,___________.
6.图,三条平行直线把平面分成I.II.III.IV四个区域(不含边界),且直线到的距离相等。点O在直线上,点A.B在直线上,P为平面区域内一点,且,给出下列四个命题:
(1)若则点P位于区域I; (2)若点P位于区域II,则
(3)若点P位于区域III,则 (4)若点P位于区域IV,则
则所有正确命题的序号为__________.
7.在三棱锥中,两两垂直,且,,,则点到的重心的距离为 .
8.如上图,边长为1的正方形ABCD的顶点A,D分别在x轴,Y轴正半轴上移动,则的概率为 .
9.已知中,边上的中线长为2,若动点满足,则的最小值是__________.
10.已知点是的中位线EF上任意一点,且,实数满足的面积分别为,记,则取最大值时,的值为__________.
11.在中,D在BC边上,,, ,则 .
12.平面上有三个点A(-2,y),B(0,),C(x,y),若⊥,则动点C的轨迹方程为________.
13.在平面直角坐标系中,是坐标原点,若两定点满足,则点集所表示的区域的面积是 .
14.已知平面向量的集合到的映射为,其中为常向量,若映射满足对任意恒成立,则用坐标可能是
A. B. C. D.
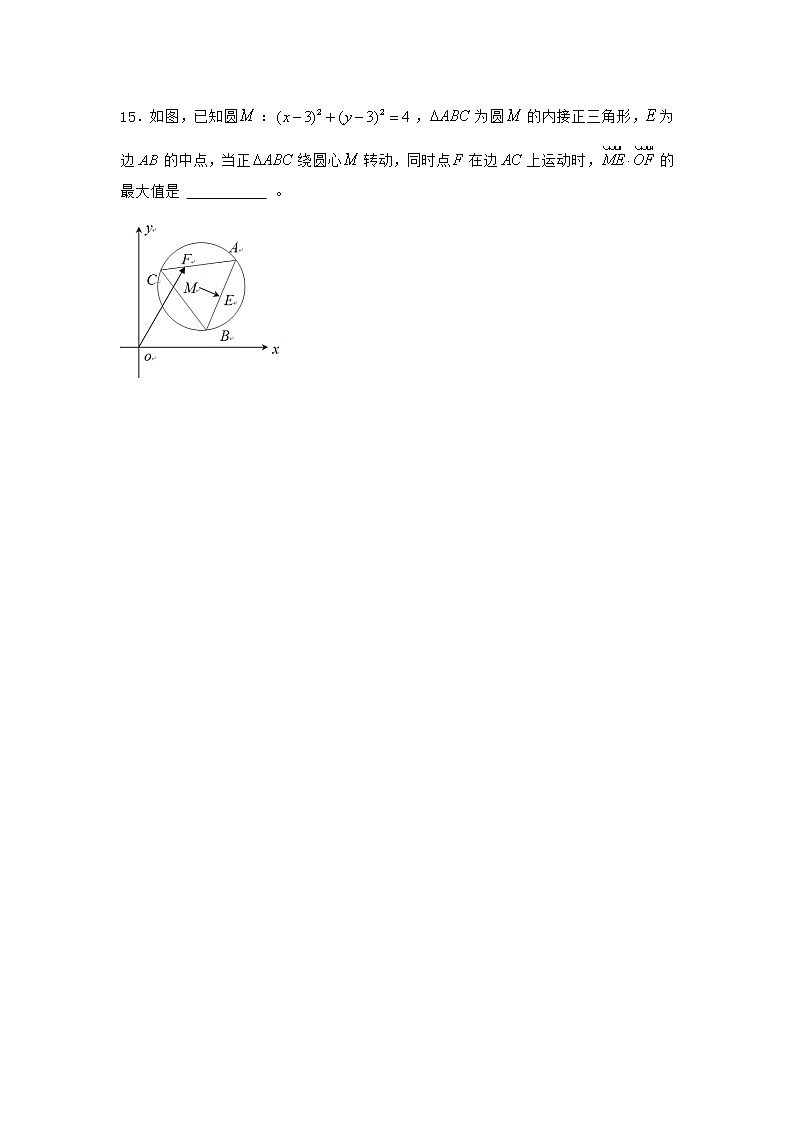
15.如图,已知圆:,为圆的内接正三角形,为边的中点,当正绕圆心转动,同时点在边上运动时,的最大值是 。
参考答案与试题解析
1.【答案】-1或2
【解析】∵l的方向向量为(-2,m),
∴-2×1-m(1-m)=0,∴m=-1或2.
2.【答案】
【解析】因为=(4,3),2+=(3,18),所以=(),
==,
3.【答案】-1
【解析】
4.【答案】
【解析】
5.【答案】;
【解析】
6.【答案】(1)(3)(4)
【解析】
7.【答案】
【解析】以PA.PB.PC为过同一顶点的三条棱,构造长方体,以CP为x轴,以CD为y轴,以CG为z轴,建立空间直角坐标系,利用向量法求解.根据题意,
解:以PA.PB.PC为过同一顶点的三条棱,作长方体如图,以CP为x轴,以CD为y轴,以CG为z轴,建立空间直角坐标系,∵PA=1,PB=2,PC=3,∴P(3,0,0),A(3,0,1),B(2,3,0),C(0,0,0),根据平面的法向量来得到点P到平平面的距离,然后根据重心的位置,结合勾股定理来得到点到的重心的距离为。故答案为
8.【答案】
【解析】令∠OAD=θ,由边长为1的正方形ABCD的顶点A.D分别在x轴.y轴正半轴上,可得出B,C的坐标,由此可以表示出两个向量,算出它们的内积即可。解:如图令∠OAD=θ,由于AD=1故0A=cosθ,OD=sinθ,如图∠BA x=
-θ,AB=1,故xB=cosθ+cos(-θ)=cosθ+sinθ,yB=sin(-θ)=cosθ,故=(cosθ+sinθ,cosθ),同理可求得C(sinθ,cosθ+sinθ),即=(sinθ,cosθ+sinθ),∴=(cosθ+sinθ,cosθ)?(sinθ,cosθ+sinθ)=1+sin2θ,
=1+sin2θ 的最大值是2,故的概率为
9.【答案】-2
【解析】
10.【答案】
【解析】
11.【答案】
【解析】
12.【答案】y2=8x
【解析】=(2,-),=(x,).
∵⊥,∴A·=2x-y2=0,即y2=8x.
13.【答案】
【解析】如图所示,由可知,当时,;当时,,所以;考虑到可取正负,所以点所表示的区域的面积,故.
14.【答案】
【解析】
15.【答案】
【解析】根据题意,由于圆:,为圆的内接正三角形,为边的中点,AB=,那么对于,可知使得向量的数量积达到最大值时的为
北师大版 (2019)必修 第二册6.1 余弦定理与正弦定理同步练习题: 这是一份北师大版 (2019)必修 第二册6.1 余弦定理与正弦定理同步练习题,共7页。
高中数学6.1 余弦定理与正弦定理课后练习题: 这是一份高中数学6.1 余弦定理与正弦定理课后练习题,共9页。试卷主要包含了把边长为1的正方形如图放置,,已知a=,b=,其中x∈等内容,欢迎下载使用。
数学必修 第二册6.1 余弦定理与正弦定理课后复习题: 这是一份数学必修 第二册6.1 余弦定理与正弦定理课后复习题,共6页。试卷主要包含了已知的三个顶点的坐标分别为等内容,欢迎下载使用。













