

北师大版高中数学必修第二册4-1单位圆与任意角的正弦函数、余弦函数定义课时作业5含答案
展开【优编】4.1 单位圆与任意角的正弦函数、余弦函数定义-1课时练习
一.填空题
1.已知外接圆的直径为d,,,,则___________.
2.若,则_______________________.
3.若,则___________.
4.已知,,.均为锐角,则______________.
5.已知直线与单位圆交于两点,设射线的对应的角是,则__________.
6.,则与的关系是_______ .
7.已知,则_______.
8.已知,则___________.
9.在上,满足的的取值范围是_____
10.若点与点关于轴对称,写出一个符合题意的___.
11.已知直线的倾斜角为,则___________.
12.若,为钝角,则的值为___________(用表示).
13.已知是第二象限角,且,_________.
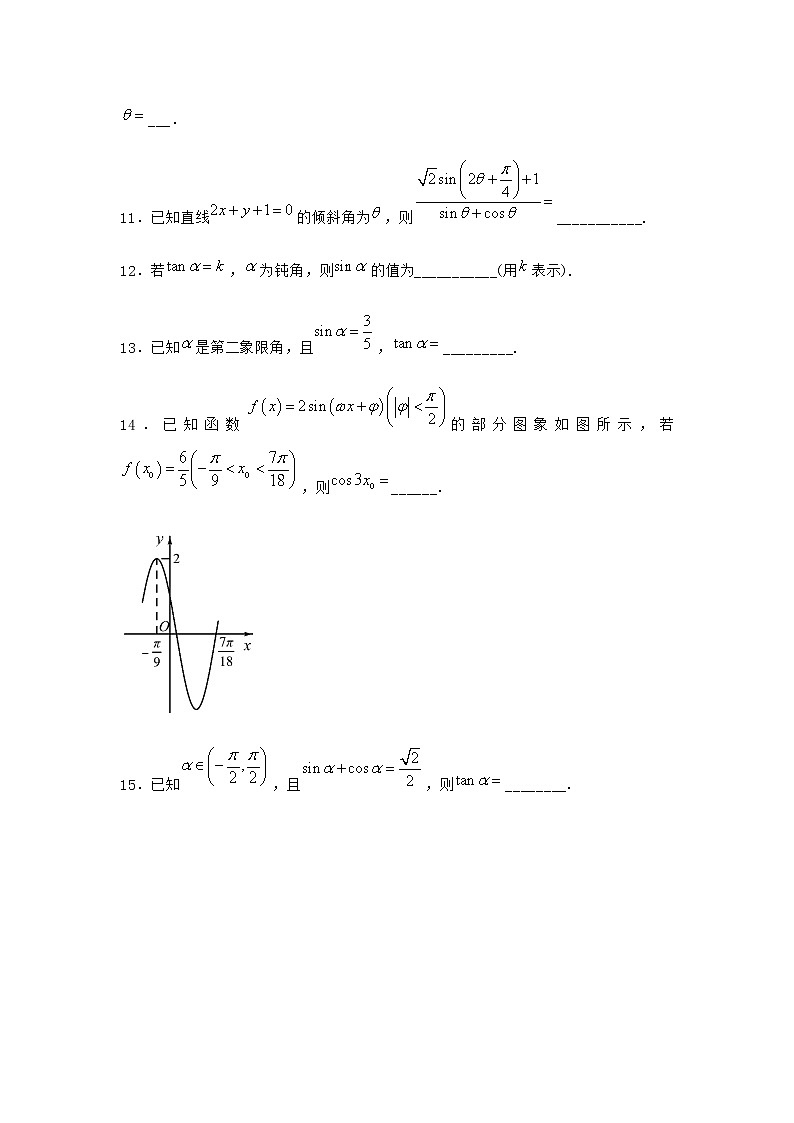
14.已知函数的部分图象如图所示,若,则______.
15.已知,且,则________.
参考答案与试题解析
1.【答案】
【解析】分析:根据余弦定理,求得,根据同角三角函数的关系,求得,利用正弦定理,即可求得答案.
详解:由余弦定理得:,
所以,
由正弦定理得.
故答案为:
2.【答案】
【解析】分析:利用同角三角函数的基本关系式进行化简求值.
详解:因为,
所以.
故答案为:
3.【答案】或
【解析】分析:由结合二倍角的正弦公式和弦化切可得出关于的方程,进而可解得的值.
详解:,
整理可得,解得或.
故答案为:或.
4.【答案】
【解析】分析:本题首先可根据同角三角函数关系得出.,然后根据两角差的余弦公式得出,最后通过二倍角公式即可得出结果.
详解:因为,,.均为锐角,
所以,,
则
,
,
故答案为:.
【点睛】
关键点点睛:本题考查同角三角函数关系.两角差的余弦公式以及二倍角公式,可通过进行简便计算,考查计算能力,是中档题.
5.【答案】
【解析】分析:设,由得到,再根据三角函数的定义由求解.
详解:如图所示:
设,
由,消去得,
则,
根据三角函数的定义得:,
即.
故答案为:
6.【答案】或
【解析】分析:根据正弦函数的定义及性质求解.
详解:因为,
所以终边相同或终边关于轴对称,
故或,
故答案为:或
7.【答案】2
【解析】分析:利用二倍角公式以及同角三角函数的基本关系式求得所求表达式的值.
详解:已知
.
故答案为:2
8.【答案】
【解析】分析:由两角差的正切公式求出,再用三角恒等变换求出,利用弦化切公式化为,代入即可求出结果.
详解:解: 由两角差的正切公式可得,得 ,
.
故答案为: .
9.【答案】
【解析】因为,且,所以
10.【答案】(满足即可)
【解析】分析:根据在单位圆上,可得关于轴对称,得出求解.
详解:与关于轴对称,
即关于轴对称,
,
则,
当时,可取的一个值为.
故答案为:(满足即可).
11.【答案】
【解析】分析:根据三角恒等变换的公式,化简原式,再由直线的倾斜角的定义,得到且,结合三角函数的基本关系式,即可求解.
详解:由题意,化简得,
又由直线的倾斜角为,可得且,
根据三角函数的基本关系式,可得,所以.
故答案为:
12.【答案】(亦可)
【解析】分析:由题知,再根据得,进而得.
详解:因为,为钝角,
所以,
又因为,
所以,即,
所以,
故答案为:
13.【答案】
【解析】分析:根据角所在的象限,判断正切函数的正负,从而求得结果.
详解:由是第二象限角,知,
则
故答案为:
14.【答案】
【解析】分析:根据的图象确定的最小正周期,进而确定,通过最高点的坐标及题目给定的范围求,进而得出,,然后利用拆角的思想得到,最后利用两角差的余弦公式得到结果.
详解:设的最小正周期为,则,,所以,.
,,.
若,则,,不合题意;
若,则,,结合可知,
,,
由于,,
又,则,
,
.
故答案为:.
【点睛】
方法点睛:根据三角函数或的部分图象求函数解析式的方法:
(1)求.,;
(2)求出函数的最小正周期,进而得出;
(3)取特殊点代入函数可求得的值.
15.【答案】
【解析】分析:已知等式平方求得,利用可解得,注意由已知条件判断出,从而得正确结论.
详解:因为,所以,,
又,所以,所以,即.
所以,解得.
又,,而,所以.
所以.
故答案为:.
【点睛】
易错点睛:本题考查同角间的三角函数关系,解题中注意角的范围的判断,函数值范围判断,否则会出现错误.本题在平方求得积后确定,实际上这个范围还显得有点大,因为从的角度可得出.实际上,在平面直角坐标系中,满足的角的终边在直线的右上方.









