

高中数学北师大版 (2019)必修 第二册4.3 诱导公式与对称课堂检测
展开【特供】4.3 诱导公式与对称-2作业练习
一.填空题
1.已知,则的值为____________.
2.角的终边在直线上,且,若是角终边上一点,O为原点,,则________.
3.在中,角为直角,线段上的点满足,若对于给定的是唯一确定的,则_______.
4.若点在角的终边上,且满足,则________.
5.若,则__________.
6.当时,的取值范围是_________.
7.已知,则______.
8.已知,则的值为_______.
9.已知,则______.
10.已知,则____________.
11.已知角终边上一点P的坐标为,则________.
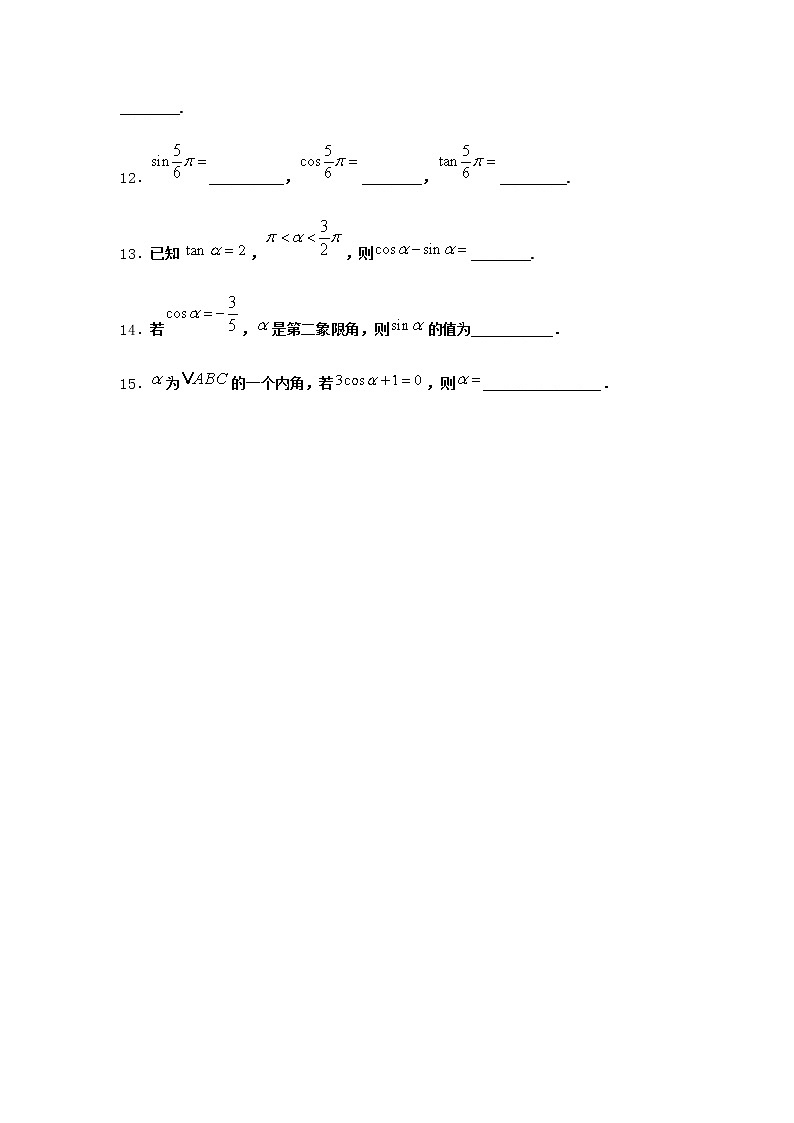
12.__________,________,_________.
13.已知,,则________.
14.若,是第二象限角,则的值为___________.
15.为的一个内角,若,则________________.
参考答案与试题解析
1.【答案】
【解析】由已知式求出,利用同角三角函数间的平方关系和商数关系,将化为,代入即可求值.
详解:,
,
则
.
故答案为:.
【点睛】
本题考查了同角三角函数间的平方关系和商数关系,正.余弦其次式的计算,二倍角的正弦公式,属于中档题.
2.【答案】2
【解析】由题意可得,,解方程组即可得到答案.
详解:因为是角终边上一点,所以,又,
所以,解得,又,所以,
,所以.
故答案为:2
【点睛】
本题考查三角函数的定义,考查学生对概念的理解和基本数学计算能力,是一道容易题.
3.【答案】
【解析】设,根据已知先求出x的值,再求的值.
【详解】
设,则.
依题意,若对于给定的是唯一的确定的,
函数在(1,)是增函数,在(,+)是减函数,
所以,此时,.
故答案为
【点睛】
本题主要考查对勾函数的图像和性质,考查差角的正切的计算和同角的三角函数的关系,意在考查学生对这些知识的理解掌握水平和分析推理能力.
4.【答案】
【解析】由正弦定义及可得到x的值,再利用计算即可.
详解:由正弦的定义,知,又,解得,
所以
故答案为:
【点睛】
本题考查利用定义法求三角函数值,考查学生的基本计算能力,是一道容易题.
5.【答案】
【解析】由及,消得到,再结合即可得到答案.
详解:由已知,及,可得,即,
又所以,.
故答案为:
【点睛】
本题主要考查三角函数的基本关系的应用,考查学生的数学运算能力,是一道容易题.
6.【答案】
【解析】根据反三角函数的知识,求得的取值范围.
详解:由于,所以,所以.
故答案为:
【点睛】
本小题主要考查反三角函数,属于基础题.
7.【答案】
【解析】分子分母同时除以,把目标式转为的表达式,代入可求.
详解:,则.
故答案为:.
【点睛】
本题考查三角函数的化简求值,常用方法:(1)弦切互化法:主要利用公式,形如等类型可进行弦化切;(2)“1”的灵活代换和的关系进行变形.转化.
8.【答案】5
【解析】由齐次式化简方法,即可得关于的方程,解方程即可求得的值.
详解:根据齐次式化减法方法,将式子上下同时除以可得
变形可得
解得
故答案为:
【点睛】
本题考查了齐次式的化简求值,属于基础题.
9.【答案】7
【解析】由已知利用同角三角函数基本关系式即可求解.
【详解】
解:,
,
故答案为:7.
【点睛】
本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用,属于基础题.
10.【答案】
【解析】先改变的形式为,再上下同除,整理后,代入即可
详解:由题,因为,则,上下同除,则可得到,将代入可得
故答案为
【点睛】
本题考查三角函数的化简求值,考查正切与正弦.余弦的关系,考查的应用
11.【答案】1
【解析】容易知道点P的坐标,根据三角函数的定义,求得和,即可求解.
【详解】
因为,,则点坐标为;
由三角函数的定义可得:
,故:
.
故答案为:1.
【点睛】
本题考查三角函数的定义,属基础题.
12.【答案】
【解析】直接利用诱导公式计算即可得到答案.
详解:,,
.
故答案为:;;
【点睛】
本题考查利用诱导公式求特殊三角函数值,考查学生的基本计算能力,是一道容易题.
13.【答案】
【解析】由平方关系以及商数关系得出,即可得出.
【详解】
由以及
得出
故答案为:
【点睛】
本题主要考查了平方关系以及商数关系,属于基础题.
14.【答案】
【解析】利用同角三角函数的基本关系式求得的值.
详解:由于,是第二象限角,所以.
故答案为:
【点睛】
本小题主要考查同角三角函数的基本关系式,属于基础题.
15.【答案】
【解析】先求出,再利用反三角函数表示.
详解:解:由已知得,
则为钝角,
.
故答案为:.
【点睛】
本题考查利用反三角函数表示角,是基础题.
北师大版 (2019)必修 第二册4.3 诱导公式与对称课后练习题: 这是一份北师大版 (2019)必修 第二册4.3 诱导公式与对称课后练习题,共12页。试卷主要包含了化简___________.,已知,且,则________., =_________;,若,则________.,已知,则__________,已知,则__________.等内容,欢迎下载使用。
高中数学北师大版 (2019)必修 第二册第一章 三角函数4 正弦函数和余弦函数的概念及其性质4.3 诱导公式与对称同步测试题: 这是一份高中数学北师大版 (2019)必修 第二册第一章 三角函数4 正弦函数和余弦函数的概念及其性质4.3 诱导公式与对称同步测试题,共12页。试卷主要包含了__________.,若则______,已知,则的值为______.,若,则__________.等内容,欢迎下载使用。
北师大版 (2019)必修 第二册第一章 三角函数4 正弦函数和余弦函数的概念及其性质4.3 诱导公式与对称同步达标检测题: 这是一份北师大版 (2019)必修 第二册第一章 三角函数4 正弦函数和余弦函数的概念及其性质4.3 诱导公式与对称同步达标检测题,共12页。试卷主要包含了化简,已知,则的值________,已知,,则________.,已知,则__________等内容,欢迎下载使用。













