小学数学苏教版六年级下册二 圆柱和圆锥精品习题

这是一份小学数学苏教版六年级下册二 圆柱和圆锥精品习题，共18页。试卷主要包含了计算下面圆柱的表面积和体积，求下面圆柱的体积，计算下面图形的体积，求圆柱的表面积和体积，求体积，计算圆柱的表面积和体积，求下面圆柱的表面积，计算零件的体积等内容，欢迎下载使用。
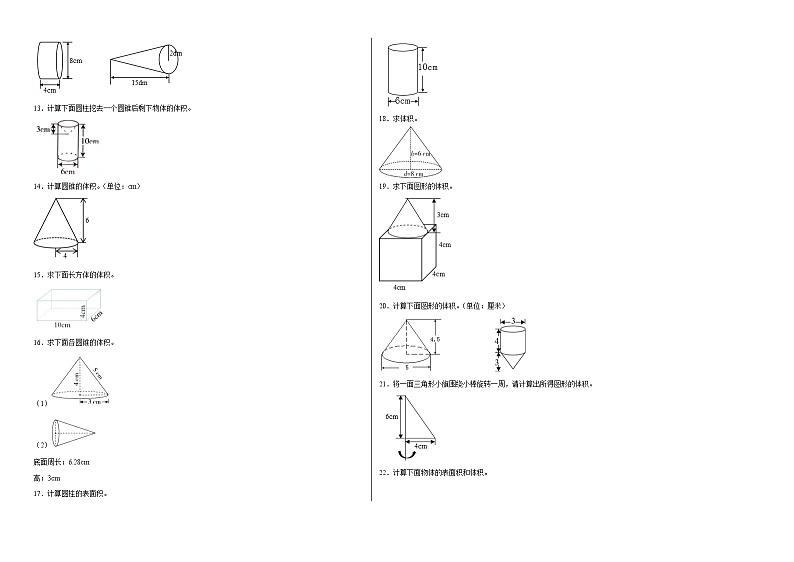
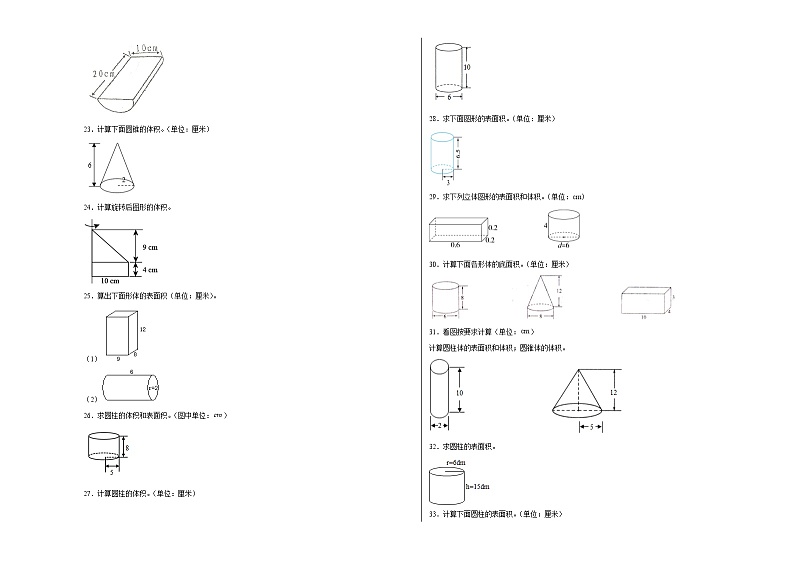
第二单元圆柱和圆锥计算题（易错题提高卷）六年级下册数学专项培优卷（苏教版）姓名：___________班级：___________考号：___________ 1．计算下面圆柱的表面积和体积。（单位：cm）2．求下面圆柱的体积。3．计算下面图形的体积。（单位：cm）4．求圆柱的表面积和体积。（单位：厘米） 5．求体积。6．计算圆柱的表面积和体积。（单位：cm） 7．求（1）的表面积和体积，求（2）的体积。（单位：cm）（1）   （2）8．求下面圆柱的表面积。底面周长：31.4cm高：6cm9．计算零件的体积。（单位：分米）10．求下面图形的表面积。（单位：厘米）11．求圆锥体积。12．计算下面圆柱的表面积及圆锥的体积。13．计算下面圆柱挖去一个圆锥后剩下物体的体积。14．计算圆锥的体积。（单位：cm）15．求下面长方体的体积。16．求下面各圆锥的体积。（1）   （2）底面周长：6.28cm高：3cm17．计算圆柱的表面积。   18．求体积。19．求下面图形的体积。20．计算下面图形的体积。（单位：厘米）                        21．将一面三角形小旗围绕小棒旋转一周，请计算出所得图形的体积。22．计算下面物体的表面积和体积。23．计算下面圆锥的体积。（单位：厘米）24．计算旋转后图形的体积。25．算出下面形体的表面积（单位：厘米）。（1）（2）26．求圆柱的体积和表面积。（图中单位：）27．计算圆柱的体积。（单位：厘米）28．求下面图形的表面积。（单位：厘米）29．求下列立体图形的表面积和体积。（单位：cm）                       30．计算下面各形体的底面积。（单位：厘米）31．看图按要求计算（单位：）计算圆柱体的表面积和体积；圆锥体的体积。32．求圆柱的表面积。33．计算下面圆柱的表面积。（单位：厘米）34．（1）求阴影部分的面积。（单位：厘米）（2）计算零件的体积。（单位：分米）35．计算下图圆柱的表面积和圆锥的体积。36．如图，把一根圆柱木料沿底面直径平均锯成两半。求这半个圆柱木料的表面积与体积。37．求下面图形的体积。 38．求出下面图形体积。  39．计算如图所示的半圆模型的表面积。（π取3.14）40．计算下面图形的体积。（单位：厘米）41．求圆柱的体积。（单位：cm）42．求下面图形的体积。（单位：厘米）43．求下面圆柱的侧面积和体积。 
参考答案：1．533.8平方厘米；942立方厘米【分析】直接运用圆柱表面积和体积公式代入数据计算即可。【详解】表面积：3.14×5²×2＋3.14×5×2×12＝157＋376.8＝533.8（平方厘米）体积：3.14×5²×12＝78.5×12＝942（立方厘米）圆柱表面积和体积公式熟练运用为本题重点。2．75.36立方厘米【分析】根据圆柱体积公式：代入数据求出体积即可。【详解】3.14×（4÷2）×6＝3.14×4×6＝75.36（立方厘米）此题主要考查学生对圆柱体积公式的实际应用解题能力，牢记公式是解题的关键。3．251.2立方厘米；75.36立方厘米【分析】根据圆柱体积公式：V＝sh和圆锥体积公式V＝sh，代入数据即可解答。【详解】（1）3.14×4²×5＝50.24×5＝251.2（立方厘米）（2）×3.14×3²×8＝9.42×8＝75.36（立方厘米）4．表面积是169.56平方厘米；体积为169.56立方厘米【分析】圆柱的表面积：侧面积＋两个底面面积；圆柱的体积：底面积×高。据此解答。【详解】表面积：6÷2＝3（厘米）3.14×32＝3.14×9＝28.26（平方厘米）28.26×2＋3.14×6×6＝56.52＋18.84×6＝56.52＋113.04＝169.56（平方厘米）体积：28.26×6＝169.56（立方厘米） 表面积是169.56平方厘米，体积为169.56立方厘米。5．240立方厘米【分析】长方体体积的大小是指长方体占据空间的大小，等于长×宽×高，代入计算即可。【详解】10×6×4＝240（立方厘米）故答案为：240立方厘米熟练掌握长方体体积公式是解题关键。基础题，要掌握。6．150.72cm2；141.3cm3【分析】圆柱的表面积＝侧面积＋底面积×2，圆柱的侧面积＝底面周长×高，圆柱的体积＝底面积×高，据此解答。【详解】6÷2＝3（cm）表面积：3.14×32×2＋3.14×6×5＝56.52＋94.2＝150.72（cm2）体积：3.14×32×5＝28.26×5＝141.3（cm3）7．（1）324平方厘米；360立方厘米；（2）16.956立方厘米【分析】第一个图是长方体，长方体的表面积＝（长×宽＋长×高＋宽×高）×2，长方体的体积＝长×宽×高，代入数据即可求解；第二个图是一个圆柱体和一个圆锥体的组合，圆柱的体积＝底面积×高，圆锥的体积＝×底面积×高，代入数据即可求解。【详解】（1）表面积：（12×5＋12×6＋6×5）×2＝（60＋72＋30）×2＝162×2＝324（平方厘米）体积：12×6×5＝12×30＝360（立方厘米）（2）半径：3÷2＝1.5（厘米），3.14×1.5×1.5×2＋×3.14×1.5×1.5×1.2＝3.14×1.5×1.5×（2＋0.4）＝7.065×2.4＝16.956（立方厘米）解决此题的关键是熟练掌握长方体的表面积和体积公式以及圆柱、圆锥的体积公式。8．345.4cm²【分析】先由底面周长是31.4cm，求出圆柱的底面半径，再利用S＝Ch＋2r求得表面积是多少即可。【详解】31.4÷3.14÷2＝10÷2＝5（厘米）31.4×6＋2×3.14×5＝188.4＋157＝345.4（cm²）本题主要考查对圆柱的侧面积、表面积公式的综合应用，首先要熟记这些公式，然后是灵活运用这些公式，通过计算就可以这道题的答案了。9．15.14立方分米【分析】组合体的体积＝长方体的体积＋圆锥的体积。长方体体积＝长×宽×高，圆锥的体积＝底面积×高×，据此代入数据，即可解答。【详解】2×2×3＋3.14×（2÷2）2×3×＝12＋3.14×1×3×＝12＋3.14＝15.14（立方分米）10．249平方厘米【分析】根据长方体表面积公式：（长×宽＋长×高＋宽×高）×2，代入数值即可解答。【详解】（8×5＋8×6.5＋6.5×5）×2＝（40＋52＋32.5）×2＝124.5×2＝249（平方厘米）此题主要考查学生利用长方体表面积公式解答问题的能力，牢记公式是解题的关键。11．188.4dm3【分析】根据圆锥的体积公式：体积＝底面积×高×，代入数据，即可解答。【详解】3.14×62×5×＝3.14×36×5×＝113.04×5×＝565.2×＝188.4（dm3）12．（1）200.96cm2；（2）62.8dm3【分析】（1）圆柱的表面积＝侧面积＋底面积×2＝πdh＋2πr2，据此代入数据计算；（2）圆锥的体积＝底面积×高×＝πr2h，据此解答。【详解】（1）3.14×8×4＋（8÷2）2×3.14×2＝3.14×32＋3.14×32＝100.48＋100.48＝200.96（cm2）（2）×3.14×22×15＝3.14×20＝62.8（dm3）13．254.34立方厘米【分析】由图意知：从一个底面直径为6厘米，高是10厘米的圆柱中挖去一个同底、高为3厘米的圆锥。用圆柱的体积减速圆锥的体积，本题即可得解。【详解】圆柱的体积：＝＝＝282.6（立方厘米）圆锥的体积：＝＝9.42×3＝28.26（立方厘米）剩下物体的体积：282.6－28.26＝254.34（立方厘米）14．100.48cm3【分析】已知圆锥的底面半径和高，求体积。利用圆锥的体积公式V＝Sh，将相关数据代入认真计算即可。【详解】3.14×4×4×6×＝50.24×（6×）＝50.24×2＝100.48（cm3）15．240立方厘米【分析】根据长方体体积公式：长×宽×高，代入数据求出体积即可。【详解】10×4×6＝40×6＝240（立方厘米）此题主要考查学生对长方体体积公式的实际应用解题能力，牢记公式是解题的关键。16．（1）37.68cm³（2）3.14 cm³【分析】（1）圆锥的体积公式：S＝rh，直接代入数据计算即可得解；（2）已知圆锥的底面周长是6.28cm和高是3cm，首先求出圆锥的底面半径，然后求出圆锥的底面积，再乘高乘即可。【详解】（1）×3.14×3×4＝×3.14×9×4＝37.68（cm³）（2）6.28÷3.14÷2＝2÷2＝1（cm）×3.14×1×3＝×3.14×1×3＝3.14 （cm³）本题主要考查圆锥的体积计算公式和圆周长公式运用，要求圆锥的体积，需要求出底面积，进而求出体积，代入公式不要忘记乘即可。17．244.92cm³【分析】圆柱的表面积是两个底面积加上侧面积，根据圆面积公式计算底面积，用底面周长乘高求出侧面积。【详解】3.14×（6÷2）2×2＋3.14×6×10＝3.14×18＋3.14×60＝56.52＋188.4＝244.92（cm3）18．100.48立方厘米【分析】根据圆锥体的体积公式：×底面积×高，代入数据，即可解答。【详解】×3.14×（8÷2）2×6＝×3.14×16×6＝×50.24×6＝50.24×2＝100.48（立方厘米）19．76.56cm3【分析】观察图形可知，图形的体积＝棱长是4cm的正方体的体积＋底面直径是4cm，高是3cm的圆锥的体积，根据正方体体积公式：体积＝棱长×棱长×棱长；圆锥的体积公式：体积＝底面积×高×，代入数据，即可解答。【详解】4×4×4＋3.14×（4÷2）2×3×＝16×4＋3.14×4×3×＝64＋12.56×3×＝64＋37.68×＝64＋12.56＝76.56（cm3）20．（1）29.4375立方厘米；（2）35.325立方厘米【分析】（1）利用圆锥体积公式进行解答即可；（2）利用圆锥体积公式：和圆柱体积公式：即可求出组合图形体积。【详解】（1）3.14×（5÷2）×4.5×＝3.14×6.25×4.5×＝19.625×4.5×＝29.4375（立方厘米）（2）3.14×（3÷2）×3×＋3.14×（3÷2）×4＝3.14×2.25×3×＋3.14×2.25×4＝7.065＋28.26＝35.325（立方厘米）此题主要考查了学生对圆锥和圆柱体积公式的应用，熟练运用公式是解题的关键。21．100.48 cm3【分析】以这个直角三角形的6cm的直角边为轴旋转可形成底面半径为4cm，高为6cm的圆锥，根据圆锥的体积计算公式“V＝πr2h”即可求出它的体积。【详解】3.14×42×6×＝3.14×16×2＝100.48（cm3）此题主要是考查圆锥的体积计算，关键是明白所形成的圆锥的底面半径及高，以直角三角形的一直角边为轴旋转一周形成的圆锥的高是为轴旋转的直角边，另一直角边为底面半径。22．592.5平方厘米，785立方厘米。【分析】（1）这时图形的表面积＝圆柱一个底面积＋侧面积的一半＋长方形切面的面积，然后根据圆的面积公式是：S＝πr2，长方形的面积公式：S＝ab，圆柱的侧面积公式：S＝Ch，把数据带入公式解答即可；（2）先根据圆柱的体积：V＝Sh，求出体积，再除以2即可。【详解】半径：10÷2＝5（厘米）表面积∶10×20＋3.14×5×5＋3.14×10×20÷2＝200＋78.5＋314＝278.5＋314＝592.5（平方厘米）体积∶3.14×5×5×20÷2＝785（立方厘米）该题关键是从整体上考虑，理解它们是有几部分构成；熟练掌握圆的面积公式，长方形的面积公式，圆柱侧面积公式以及圆柱的体积公式是解题的关键。23．25.12立方厘米【分析】根据圆锥体积公式计算即可。【详解】×3.14×2×6＝25.12（立方厘米）本题考查了圆锥体积，圆锥体积＝底面积×高×。24．2198cm³【分析】旋转后得到一个圆柱和圆锥的组合体，圆柱、圆锥的底面半径均是10厘米，圆柱的高是4厘米，圆锥的高是9厘米。将数据带入圆柱、圆锥的体积公式计算即可。【详解】3.14×10²×4＋×3.14×10²×9＝314×4＋314×3＝1256＋942＝2198（cm³）25．（1）552平方厘米；（2）100.48平方厘米【分析】（1）根据长方体的表面积计算公式进行计算，长方体的表面积＝（长×宽＋长×高＋宽×高）×2；（2）圆柱的表面积＝底面积×2＋侧面积，侧面积＝底面周长×高。据此计算。【详解】（1）（9×8＋9×12＋8×12）×2＝（72＋108＋96）×2＝276×2＝552（平方厘米）（2）3.14×22×2＋3.14×2×2×6＝25.12＋75.36＝100.48（平方厘米）26．表面积：408.2cm2；体积：628cm3【分析】根据圆柱的表面积公式：底面积×2＋侧面积；圆柱的体积：底面积×高，代入数据，即可解答。【详解】表面积：3.14×52×2＋3.14×5×2×8＝3.14×25×2＋15.7×2×8＝78.5×2＋31.4×8＝157＋251.2＝408.2（cm2）体积：3.14×52×8＝3.14×25×8＝78.5×8＝628（cm3）27．282.6立方厘米【分析】圆柱的底面直径是6厘米，除以2得半径3厘米，再利用圆柱的体积公式：V＝Sh，进而求得圆柱的体积。据此解答。【详解】6÷2＝3（厘米）3×3×3.14×10＝90×3.14＝282.6（立方厘米）28．178.98平方厘米【分析】圆柱表面积公式：S＝2πrh＋2πr²，代入数据解答即可。【详解】2×3.14×3×6.5＋2×3.14×32＝122.46＋56.52＝178.98（平方厘米）考查了圆柱的表面积，注意根据公式代入数据，计算时要认真。29．0.56cm2；0.024cm3131.88cm2；113.04cm3【分析】（1）根据长方体的表面积S=2（ab+ac+bc）、长方体的体积V=abh，列式计算即可；（2）圆柱的表面积=2πrh+2πr2，圆柱的体积=πr2h，据此代入数据即可解答。【详解】表面积：（0.2×0.6＋0.2×0.6＋0.2×0.2）×2＝0.28×2＝0.56（cm2）体积：0.6×0.2×0.2＝0.024（cm3）表面积：3.14×6×4＋3.14×（6÷2）2×2＝75.36+56.52＝131.88（cm2）体积：3.14×（6÷2）2×4＝113.04（cm3）此题考查了长方体、圆柱体的表面积、体积公式的计算应用，熟记公式即可解答。30．（1）28.26平方厘米；（2）50.24平方厘米；（3）40平方厘米。【分析】（1）圆柱的底面是一个圆，即求圆的面积，圆的面积公式：π×半径×半径；（2）圆锥的底面是一个圆，即求圆的面积，圆的面积公式：π×半径×半径；（3）长方体的底面是一个长方形，即求长方形的面积，长方形面积=长×宽。【详解】（1）圆的半径：6÷2＝3（厘米），圆的面积：3.14×3×3＝3.14×9＝28.26（平方厘米）（2）圆的半径：8÷2＝4（厘米）圆的面积：3.14×4×4＝3.14×16＝50.24（平方厘米）（3）10×4＝40（平方厘米）此题考查的是圆柱、圆锥和长方体的特征，需熟练掌握圆的面积和长方形的面积公式才是解题关键。31．69.08平方厘米；31.4立方厘米； 314立方厘米【分析】圆柱的底面直径已知，根据圆柱的表面积公式：、圆柱的体积公式：；圆锥的底面半径已知，圆锥的体积公式：，将数值代入公式即可。【详解】圆柱的表面积： （平方厘米圆柱的体积：（立方厘米）圆锥的体积：（立方厘米）32．791.28dm2【分析】圆柱的表面积＝侧面积＋底面积×2，将数据代入公式，即可求出圆柱的表面积。【详解】2×3.14×6×15＋3.14×6×6×2＝565.2＋226.08＝791.28（dm2）33．169.56平方厘米【分析】根据圆柱表面积公式，列式计算即可。【详解】3.14×（6÷2）2×2＋3.14×6×6＝56.52＋113.04＝169.56（平方厘米）本题考查了圆柱表面积，圆柱表面积＝底面积×2＋侧面积。34．（1）平方厘米（2）立方分米【分析】（1）观察图形可知，阴影部分面积＝上底是4厘米，下底是6厘米，高是（4＋6）厘米的梯形面积－底是6厘米，高是6厘米的三角形面积－半径是4厘米圆的面积的；根据梯形的面积公式：面积＝（上底＋下底）×高÷2；三角形面积公式：面积＝底×高÷2；圆的面积公式：面积＝π×半径2；代入数据，即可解答；（2）组合体的体积＝长2分米，宽2分米，高是3分米的长方体体积＋底面直径是2分米，高是3分米的圆锥的体积，根据长方体体积公式：体积＝长×宽×高，圆锥的体积公式：体积＝底面积×高×；代入数据，即可解答。【详解】（4＋6）×（4＋6）÷2－6×6÷2－3.14×42×＝10×10÷2－36÷2－3.14×16×＝100÷2－18－50.24×＝50－18－12.56＝32－12.56＝19.44（平方厘米）（2）2×2×3＋3.14×（2÷2）2×3×＝4×3＋3.14×1×3×＝12＋3.14×3×＝12＋9.42×＝12＋3.14＝15.14（立方分米）35．150.72平方厘米；100.48立方厘米【分析】圆柱的表面积等于底面的周长乘高再加上两个底面的面积；圆锥的体积＝×底面积×高，据此解答。【详解】3.14×（3×2）×5＋3.14×32×2＝3.14×30＋3.14×18＝3.14×48＝150.72（平方厘米）×3.14×（8÷2）2×6＝3.14×16×2＝100.48（立方厘米）36．5.2656平方米；0.314立方米【分析】观察图形可知，半个圆柱木料的表面积包含一个圆柱底面积、半个圆柱侧面积以及一个长为5m，宽为4dm的长方形面积；半个圆柱木料的体积正好是圆柱体积的一半，据此解答即可。【详解】4分米＝0.4米表面积：0.4×5＋3.14×（0.4÷2）2＋3.14×0.4×5÷2＝2＋0.1256＋3.14＝5.2656（平方米）体积：3.14×（0.4÷2）2×5÷2＝3.14×0.04×5÷2＝0.618÷2＝0.314（立方米）本题主要考查了圆柱体积和面积的实际应用问题。37．15.7立方厘米【分析】这个图形的体积＝圆柱体积－圆锥体积，圆柱体积＝底面积×高，圆锥体积＝底面积×高×。【详解】2÷2＝1（分米）12×3.14×6＝18.84（立方分米）×12×3.14×3＝3.14（立方分米）18.84－3.14＝15.7（立方分米）38．50.24立方厘米；100.48立方分米【分析】将数据代入圆柱的体积公式：V＝πr2h及圆锥的体积公式：V＝πr2h计算即可。【详解】V＝πr2h＝3.14×22×4＝12.56×4＝50.24（立方厘米）V＝πr2h＝×3.14×42×6＝50.24×2＝100.48（立方分米）39．15162平方厘米【分析】通过观察图形可知，半圆模型的表面积是由两个半圆面积加一半的圆柱侧面积加长方形面积组成，代数进行解答即可。【详解】6分米＝60厘米3.14×（60÷2）＋3.14×60×80÷2＋60×80＝2826＋7536＋4800＝15162（平方厘米）此题主要考查学生对圆柱表面积的理解与灵活应用，需要牢记圆柱表面积公式：和长方形面积公式：长×宽。40．310.86立方厘米【分析】由图可知组合体由底面直径是6厘米，高为8厘米的圆锥、底面直径是6厘米，高为5厘米的圆柱、底面直径是6厘米，高是10厘米的圆锥三部分组成，根据圆柱的体积公式：V＝πr2h，及圆锥的体积公式：V＝πr2h，带入数据计算即可。【详解】×3.14×（6÷2）2×8＋3.14×（6÷2）2×5＋×3.14×（6÷2）2×10＝3.14××9×8＋3.14×9×5＋3.14××9×10＝3.14×（24＋45＋30）＝3.14×99＝310.86（立方厘米）本题主要考查圆柱、圆锥体积公式的应用，解题时不要忘记圆锥的体积公式的。41．150.72cm3【分析】根据圆的周长公式：C＝2πr可知：r＝C÷2π，代入数据求出半径。再将数据带入圆柱的体积公式：V＝πr2h计算即可。【详解】12.56÷3.14÷2＝4÷2＝2（cm）3.14×22×12＝3.14×48＝150.72（cm3）42．329.7立方厘米【分析】根据圆柱的体积公式：，圆锥的体积公式：，把数据代入公式求出它们的体积和即可。【详解】＝3.14×9×10＋×3.14×9×5＝282.6＋47.1＝329.7（立方厘米）43．188.4cm²；282.6cm³【分析】先根据圆的周长＝直径×圆周率，计算出圆柱的底面周长，再根据圆柱的侧面积＝圆柱的底面周长×高；圆柱的体积＝底面积×高；据此解答。【详解】侧面积：3.14×6×10＝18.84×10＝188.4（cm²）体积：3.14×（6÷2）×10＝3.14×9×10＝282.6（cm³）所以圆柱的侧面积为188.4cm²，体积为282.6cm³。本题主要考查了圆柱的侧面积的体积的计算方法及其应用。圆柱的侧面是一个曲面，展开后是一个长方形，长方形的长等于圆柱的底面周长，宽等于圆柱的高，所以圆柱的侧面积等于底面周长乘高。