2022-2023学年浙江省杭州市八年级下册数学第一次月考模拟卷（卷一卷二）含解析

这是一份2022-2023学年浙江省杭州市八年级下册数学第一次月考模拟卷（卷一卷二）含解析，共49页。试卷主要包含了 函数的图象过点， 圆周率π=3， 在实数,－,，0等内容，欢迎下载使用。
2022-2023学年浙江省杭州市八年级下册数学第一次月考模拟卷（卷一）
一.选一选（每题3分，共18分）
1. 今年我市有近2万名考生参加中考，为了解这些考生的数学成绩，从中抽取1000名考生的数学成绩进行统计分析，以下说确的是（ ）
A. 这1000名考生是总体一个样本 B. 近2万名考生是总体
C. 每位考生的数学成绩是个体 D. 1000名学生是样本容量
2. 如图，∠CAB＝∠DBA，再添加一个条件，没有一定能判定△ABC≌△BAD的是（ ）

A AC＝BD B. ∠1＝∠2 C. ∠C＝∠D D. AD＝BC
3. 下列条件中，没有能判断△ABC为直角三角形的是　　　（ ）
A. a=1.5 b=2 c=2.5 B. a：b：c=5：12：13
C. ∠A＋∠B=∠C D. ∠A：∠B：∠C=3：4：5
4. 函数的图象过点（0,2），且 y随x的增大而增大，则m=（ ）
A. -1 B. 3 C. 1 D. -1或3
5. 用图象法解某二元方程组时，在同一直角坐标系中作出相应的两个函数的图象（如图所示），则所解的二元方程组是（　　）


A. B.
C. D.
6. 如图，在平面直角坐标系中，线段AB的端点坐标为A(－3，5)，B(2，3)，直线
y=kx－1与线段AB有交点，则k的值没有可能是（ ）

A. －5 B. －1 C. 3 D. 5
二.填 空 题（每题3分，共30分）
7. 如果是函数，则的值是________________.
8. 圆周率π=3.1415926…,用四舍五入法把到万分位，得到的近似值是_____.
9. 在实数,－,，0.333333333……,，0，1.732，2.010010001……中，无理数有__________个.
10. 如果点B (n2－4，－n－3) 在y轴上，那么n=_____________
11. 将直线y=2x-1向上平移2个单位得到的函数的关系式是：_______________.
12. 为了估算湖里有多少条鱼，从湖里捕上100条做上标记，然后放回湖里，一段时间待标记的鱼全混合于鱼群中后，第二次捕得200条，发现其中带标记的鱼25条，我们可以估算湖里有鱼_____条．
13. 如图，点B（﹣2，0）的直线y=kx+b与直线y=mx相交于点A（﹣1，﹣2），则关于x的没有等式组mx＜kx+b＜0的解集为________．

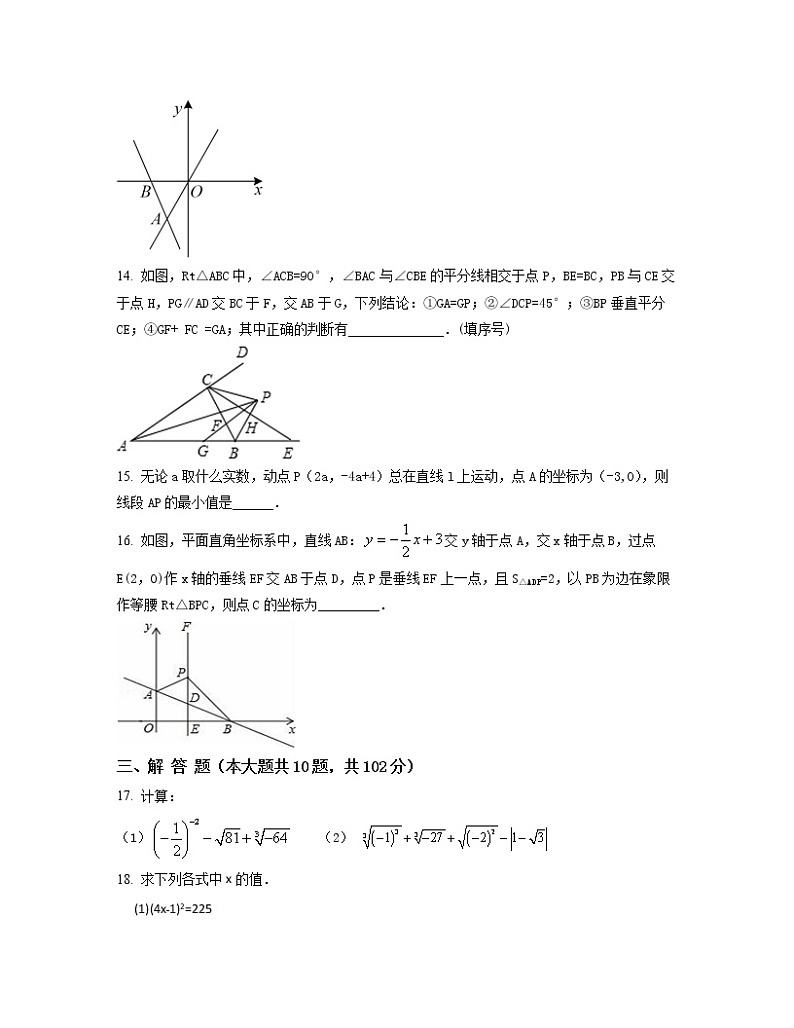
14. 如图，Rt△ABC中，∠ACB=90°，∠BAC与∠CBE的平分线相交于点P，BE=BC，PB与CE交于点H，PG∥AD交BC于F，交AB于G，下列结论：①GA=GP；②∠DCP=45°；③BP垂直平分CE；④GF+ FC =GA；其中正确的判断有______________．(填序号)

15. 无论a取什么实数，动点P（2a，-4a+4）总在直线l上运动，点A的坐标为（-3,0），则线段AP的最小值是______．
16. 如图，平面直角坐标系中，直线AB：交y轴于点A，交x轴于点B，过点E(2，0)作x轴的垂线EF交AB于点D，点P是垂线EF上一点，且S△ADP=2，以PB为边在象限作等腰Rt△BPC，则点C的坐标为_________．

三、解 答 题（本大题共10题，共102分）
17. 计算：
（1） （2）
18. 求下列各式中x的值．
(1)(4x﹣1)2=225
(2)(x﹣1)3+27=0．
19. 如图，将长方形ABCD沿着对角线BD折叠，使点C落在C′处，BC′交AD于点E．
（1）若∠DBC=25°，求∠ADC′的度数；
（2）若AB=4，AD=8，求△BDE的面积．

20. 已知函数y1＝kx＋b的图像点（0，-2），（2，2）.
（1）求函数的表达式，并在所给直角坐标系中画出此函数的图像；；
（2）根据图像回答：当x 时，y1=0；
（3）求直线y1＝kx＋b、直线y2＝-2x+4与y轴围成的三角形的面积．

21. 在如图的方格中，每个小正方形的边长都为1，△ABC的顶点均在格点上．在建立平面直角坐标系后，点B的坐标为（﹣1，2）．
（1）把△ABC向下平移8个单位后得到对应的△A1B1C1，画出△A1B1C1；
（2）画出与△A1B1C1关于y轴对称的△A2B2C2；
（3）若点P（a，b）是△ABC边上任意一点，P2是△A2B2C2边上与P对应的点，写出P2的坐标为______；
（4）试在y轴上找一点Q，使得点Q到B2、C2两点的距离之和最小，此时，QB2+QC2的最小值为______．


22. 八（1）班同学了解2015年某小区家庭月均用水情况，随机了该小区部分家庭，并将数据进行如下整理，
月均用水量(t)
频数(户)
频率

6
0.12

m
0.24

16
0.32

10
0.20

4
n

2
0.04

请解答以下问题：
（1）这里采用的方式是　　　　（填“普查”或“抽样”），样本容量是　　　　；
（2）填空： ， ，并把频数分布直方图补充完整；
（3）若将月均用水量的频数绘成扇形统计图，则月均用水量“”的圆心角的度数是　　　　；
（4）若该小区有1000户家庭，求该小区月均用水量超过10t家庭大约有多少户？
23. 如图，在△ABC中，AB=AC，DE垂直平分AB，BE⊥AC，AF⊥BC，
（1）求证：BF=EF；（2）求∠EFC的度数.

24. 平面直角坐标系中，点A的坐标为(2，4)，点B的坐标为(2，7) ，直线lA点且平行于x
轴，直线l上动点C从A点出发以每秒4个单位的速度沿直线l运动．若在x轴上有两点D、E,
连接DB、OB，连接EC、OC，满足DB＝OB，EC＝OC，设点C运动时间t秒，
(1) 如图1，若动点C从A点出发向左运动，当t＝1秒时，
①求线段BC的长和点E的坐标；
②求此时DE与AC的数量关系？
(2)探究：动点C在直线l运动，无论t取何值，是否都存在上述（1）②中的数量关系？ 若存在，请证明；若没有存在，请说明理由.

图1 图2
25. 甲，乙两人同时各接受了600个零件的加工任务，甲比乙每分钟加工的数量多，两人同时开始加工，加工过程中其中一人因故障停止加工几分钟后又继续按原速加工，直到他们完成任务，如图表示甲比乙多加工的零件数量（个）与加工时间（分）之间的函数关系，观察图象解决下列问题：
（1）点B的坐标是________，B点表示的实际意义是___________ _____；
（2）求线段BC对应的函数关系式和D点坐标；
（3）乙在加工的过程中，多少分钟时比甲少加工100个零件？
（4）为了使乙能与甲同时完成任务，现让丙帮乙加工，直到完成.丙每分钟能加工3个零件，并把丙加工的零件数记在乙的名下，问丙应在第多少分钟时开始帮助乙？并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.

26. 已知直线y＝2x－5与x轴和y轴分别交于点A和点B，点C（1，n）在直线AB上，点D在y轴的负半轴上，且CD=．
（1）求点C、点D的坐标.
（2）若P为y轴上的点，当△PCD为等腰三角形时，求点P的坐标.
（3）若点M为x轴上一动点（点M没有与点O重合），N为直线y＝2x－5上一动点，是否存在点M、N，使得△AMN与△AOB全等？若存在，求出点N的坐标；若没有存在，请说明理由．


2022-2023学年浙江省杭州市八年级下册数学第一次月考模拟卷
（卷一）
一.选一选（每题3分，共18分）
1. 今年我市有近2万名考生参加中考，为了解这些考生的数学成绩，从中抽取1000名考生的数学成绩进行统计分析，以下说确的是（ ）
A. 这1000名考生是总体的一个样本 B. 近2万名考生是总体
C. 每位考生的数学成绩是个体 D. 1000名学生是样本容量
【正确答案】C

【详解】试题分析：1000名考生的数学成绩是总体的一个样本；近8万多名考生的数学成绩是总体；每位考生的数学成绩是个体；1000是样本容量.
考点：（1）、总体；（2）、样本；（3）、个体；（4）、样本容量.
2. 如图，∠CAB＝∠DBA，再添加一个条件，没有一定能判定△ABC≌△BAD的是（ ）

A. AC＝BD B. ∠1＝∠2 C. ∠C＝∠D D. AD＝BC
【正确答案】D

【分析】根据全等三角形的判定定理（SAS，ASA，AAS，SSS）判断即可．
【详解】解答：解：A.∵AC＝BD，∠CAB＝∠DBA，AB＝AB，
∴根据SAS能推出△ABC≌△BAD，故本选项错误；
B.∵∠CAB＝∠DBA，AB＝AB，∠1＝∠2，
∴根据ASA能推出△ABC≌△BAD，故本选项错误；
C.∵∠C＝∠D，∠CAB＝∠DBA，AB＝AB，
∴根据AAS能推出△ABC≌△BAD，故本选项错误；
D.根据AD＝BC和已知没有能推出△ABC≌△BAD，故本选项正确；
故选：D．
本题考查了对全等三角形的判定定理的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．
3. 下列条件中，没有能判断△ABC为直角三角形是　　　（ ）
A. a=1.5 b=2 c=2.5 B. a：b：c=5：12：13
C. ∠A＋∠B=∠C D. ∠A：∠B：∠C=3：4：5
【正确答案】D

【详解】A. a2+b2=1.52+22=2.52=c2，所以能判断△ABC是直角三角形，故没有符合题意；
B. a：b：c=5：12：13，52+122=132，所以能判断△ABC是直角三角形，故没有符合题意；
C. ∠A＋∠B=∠C ，∠A＋∠B+∠C =180°，所以∠C=90°，△ABC是直角三角形，故没有符合题意；
D. ∠A：∠B：∠C=3：4：5，3+4≠5，所以△ABC表示直角三角形，故符合题意，
故选D.
4. 函数的图象过点（0,2），且 y随x的增大而增大，则m=（ ）
A. -1 B. 3 C. 1 D. -1或3
【正确答案】B

【详解】∵函数y=mx+|m-1|的图象过点（0，2），
∴|m-1|=2，
∴m-1=2或m-1=-2，
解得m=3或m=-1，
∵y随x的增大而增大，
∴m＞0，
∴m=3．
故选B．
5. 用图象法解某二元方程组时，在同一直角坐标系中作出相应的两个函数的图象（如图所示），则所解的二元方程组是（　　）


A. B.
C. D.
【正确答案】D

【详解】解：设过点（1，1）和（0，-1）的直线解析式为y=kx+b，
则，解得，
所以过点（1，1）和（0，-1）的直线解析式为y=2x-1；
设过点（1，1）和（0，2）的直线解析式为y=mx+n，
则，即得，
所以过点（1，1）和（0，2）的直线解析式为y=-x+2，
所以所解的二元方程组为，
故选：D．
6. 如图，在平面直角坐标系中，线段AB的端点坐标为A(－3，5)，B(2，3)，直线
y=kx－1与线段AB有交点，则k的值没有可能是（ ）

A. －5 B. －1 C. 3 D. 5
【正确答案】B

【详解】①当直线y=kx-1过点A时，将A（-3，5）代入解析式y=kx-1得，k=-2，
②当直线y=kx-1过点B时，将B（2，3）代入解析式y=kx-1得，k=2，
∵|k|越大，它的图象离y轴越近，
∴当k≥2或k≤-2时，直线y=kx-1与线段AB有交点，
纵观各选项，只有B选项符合题意，
故选B．
本题考查了两直线相交的问题，分别将A、B两点代入直线y=kx－1求出k的值，然后根据图象的特点确定出k的取值范围是解题的关键．
二.填 空 题（每题3分，共30分）
7. 如果是函数，则的值是________________.
【正确答案】-1

【详解】由题意得： ，
解得：m=-1，
故答案为-1.
8. 圆周率π=3.1415926…,用四舍五入法把到万分位，得到的近似值是_____.
【正确答案】3.1416

【分析】把十万分位上的数字9进行四舍五入得到万分位的近似值．
【详解】解：π=3.1415926…,到万分位的近似值是3.1416．
故3.1416．
本题考查了近似数和有效数字：四舍五入得到的数叫近似数；从一个近似数左边个没有为0的数数起到这个数完为止，所有数字都叫这个数的有效数字．
9. 在实数,－,，0.333333333……,，0，1.732，2.010010001……中，无理数有__________个.
【正确答案】3；

【详解】在实数，－，0.333333333……，，0，1.732，2.010010001……中，无理数有，－， 2.010010001……，共3个，
故答案为3.
10. 如果点B (n2－4，－n－3) 在y轴上，那么n=_____________
【正确答案】2/-2；

【详解】∵B（n2-4，-n-3）在y轴上，
∴n2-4=0，
解得：n=±2，
故答案为±2．
本题主要考查了点的坐标性质，得出y轴上点的坐标性质是解题关键．
11. 将直线y=2x-1向上平移2个单位得到的函数的关系式是：_______________.
【正确答案】y＝2x+1；

【详解】由“上加下减”的原则可知，直线y=2x-1向上平移2个单位，所得直线解析式是：y=2x-1+2，即y=2x+1，
故答案为y=2x+1.
12. 为了估算湖里有多少条鱼，从湖里捕上100条做上标记，然后放回湖里，一段时间待标记的鱼全混合于鱼群中后，第二次捕得200条，发现其中带标记的鱼25条，我们可以估算湖里有鱼_____条．
【正确答案】

【详解】设鱼塘里约有鱼x条，
依题意得200：25=x：100，
∴x=800，
∴估计鱼塘里约有鱼800条,
故答案为800.
13. 如图，点B（﹣2，0）的直线y=kx+b与直线y=mx相交于点A（﹣1，﹣2），则关于x的没有等式组mx＜kx+b＜0的解集为________．

【正确答案】-2