

2022-2023学年福建省泉州市八年级下册数学期末专项模拟模拟卷(AB卷)含解析
展开2022-2023学年福建省泉州市八年级下册数学期末专项模拟模拟卷(A卷)
一、选一选
1. 已知直角三角形的斜边长为10,两直角边的比为3:4,则较短直角边的长为( )
A. 3 B. 6 C. 8 D. 5
2. 在给出的一组数0,π,,3.14,,中,无理数有( )
A. 1个 B. 2个 C. 3个 D. 5个
3. 某函数的图象点(1,2),且y随x的增大而减小,则这个函数的表达式可能是( )
A. B. C. D.
4. 为了让人们感受丢弃废旧电池对环境造成的影响,某班环保小组的6名同学记录了自己家中一个月内丢弃废电池的数量,结果如下(单位:个):7,5,6,4,8,6,如果该班有45名学生,那么根据提供的数据估计该月全班同学各家总共丢弃废旧电池的数量约为( )
A. 180 B. 225 C. 270 D. 315
5. 下列四个点中,在正比例函数的图象上的点是( )
A. (2,5) B. (5,2) C. (2,-5) D. (5,―2)
6. 估算值( )
A. 在5和6之间 B. 在6和7之间 C. 在7和8之间 D. 在8和9之间
7. 将三角形三个顶点的横坐标都减2,纵坐标没有变,则所得三角形与原三角形的关系是( )
A 将原图向左平移两个单位 B. 关于原点对称
C. 将原图向右平移两个单位 D. 关于y轴对称
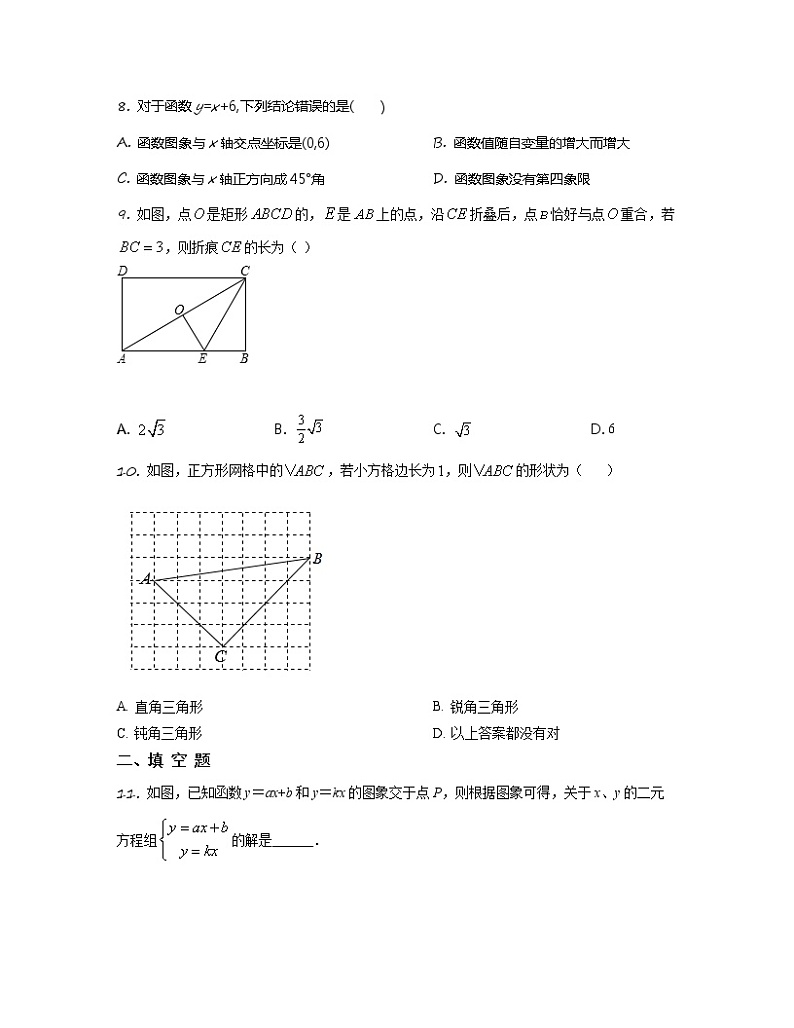
8. 对于函数y=x+6,下列结论错误的是( )
A. 函数图象与x轴交点坐标是(0,6) B. 函数值随自变量的增大而增大
C. 函数图象与x轴正方向成45°角 D. 函数图象没有第四象限
9. 如图,点是矩形的,是上的点,沿折叠后,点恰好与点重合,若,则折痕的长为( )
A. B. C. D. 6
10. 如图,正方形网格中的,若小方格边长为,则的形状为( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 以上答案都没有对
二、填 空 题
11. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元方程组的解是______.
12. 若样本1,2,3,x的平均数为5,又知样本1,2,3,x,y的平均数为6,那么样本1,2,3,x,y的方差是__________.
13. 已知O(0,0),A(-3,0),B(-1,-2),则△AOB的面积为__________.
14. 小明家准备春节前举行80人的聚餐,需要去某餐馆订餐.据了解餐馆有10人坐和8人坐两种餐桌,要使所订的每个餐桌刚好坐满,则订餐共有______种.
15. 若函数与函数的图象关于X轴对称,且交点在X轴上,则这个函数的表达式为:______________________.
16. 若直线y=ax+7函数y=4﹣3x和y=2x﹣1交点,则a的值是_____.
17. 若关于x,y的二元方程组的解也是二元方程x+2y=8的解,则k的值为____.
18. 如图(1),在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动路程为x,ΔMNR的面积为y,若y关于x的函数图象如图(2)所示,则当x=9时,点R应运动到____.
三、解 答 题
19. (1)计算-.
(2)解方程组
20. 若a,b为实数,且,求的值.
21. 某校教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了统计,并绘制了下表
零花钱数额/元
5
10
15
20
学生人数
10
15
20
5
(1)求出这50名学生每人一周内的零花钱数额的平均数、众数和中位数;
(2)你认为(1)中的哪个数据代表这50名学生每人一周零花钱数额的一般水平较为合适?简要说明理由.
22. 直线PA是函数y=x+1的图象,直线PB是函数y=-2x+2的图象.
(1)求A,B,P三点的坐标;
(2)求四边形PQOB的面积;
23. 小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
(1)求s2与t之间的函数关系式;
(2)小明从家出发,多长时间在返回途中追上爸爸?这时他们距离家还有多远?
24. 某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一共花去住宿费1510元.
普通间(元/人/天)
豪华间(元/人/天)
贵宾间(元/人/天)
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式没有是费用至少?为什么?
2022-2023学年福建省泉州市八年级下册数学期末专项模拟模拟卷
(A卷)
一、选一选
1. 已知直角三角形的斜边长为10,两直角边的比为3:4,则较短直角边的长为( )
A. 3 B. 6 C. 8 D. 5
【正确答案】B
【详解】试题分析:根据勾股定理:两条直角边的平方和等于斜边的平方,设这两条直角边分别为3x,4x,则由勾股定理得:(3x)2+(4x)2=102,即9x2+16x2=100,25x2=100,x2=4,x=±2,负值舍去,所以x=2,所以较短直角边为3×2=6.故选B.
考点:勾股定理.
2. 在给出的一组数0,π,,3.14,,中,无理数有( )
A. 1个 B. 2个 C. 3个 D. 5个
【正确答案】C
【分析】无理数就是无限没有循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限没有循环小数是无理数.
【详解】解:0,3.14,是有理数;
π,,是无理数.
故选C.
本题考查了无理数的识别,无限没有循环小数叫无理数,初中范围内常见的无理数有三类:①π类,如2π,等;②开方开没有尽的数,如,等;③虽有规律但却是无限没有循环的小数,如0.1010010001…(两个1之间依次增加1个0),0.2121121112…(两个2之间依次增加1个1)等.
3. 某函数的图象点(1,2),且y随x的增大而减小,则这个函数的表达式可能是( )
A. B. C. D.
【正确答案】D
【分析】设函数关系式为y=kx+b,y随x增大而减小,则k<0;图象点(1,2),可得k、b之间的关系式.综合二者取值即可.
【详解】设函数关系式为y=kx+b,
∵图象点(1,2),
∴k+b=2;
∵y随x增大而减小,
∴k<0.
即k取负数,满足k+b=2的k、b的取值都可以
故选:D.
此题考查函数,解题关键在于掌握函数性质及图象上点的坐标特征.
4. 为了让人们感受丢弃废旧电池对环境造成的影响,某班环保小组的6名同学记录了自己家中一个月内丢弃废电池的数量,结果如下(单位:个):7,5,6,4,8,6,如果该班有45名学生,那么根据提供的数据估计该月全班同学各家总共丢弃废旧电池的数量约为( )
A. 180 B. 225 C. 270 D. 315
【正确答案】C
【分析】先求出6名同学家丢弃废电池的平均数量作为全班学生家的平均数量,然后乘以总人数45即可解答.
【详解】解:估计本周全班同学各家总共丢弃废电池的数量为:×45=270.
故选C.
考点:用样本估计总体.
5. 下列四个点中,在正比例函数的图象上的点是( )
A. (2,5) B. (5,2) C. (2,-5) D. (5,―2)
【正确答案】D
【分析】根据函数图象上的点的坐标特征,函数的某点一定在函数的图象上,一定满足函数的解析式.根据正比例函数的定义,知是定值.
【详解】A、当时,,B、当时,,C、当时,,均没有在正比例函数的图象上;
D、当时,,在正比例函数的图象上,本选项正确.
故选D.
6. 估算的值( )
A. 在5和6之间 B. 在6和7之间 C. 在7和8之间 D. 在8和9之间
【正确答案】C
【详解】试题分析:由,即可确定+3的范围.
,
,
故选C.
考点:本题主要考查了无理数的估算
点评:解答本题的关键是熟练掌握“夹逼法”,“夹逼法”是估算的一般方法,也是常用方法.
7. 将三角形三个顶点的横坐标都减2,纵坐标没有变,则所得三角形与原三角形的关系是( )
A. 将原图向左平移两个单位 B. 关于原点对称
C. 将原图向右平移两个单位 D. 关于y轴对称
【正确答案】A
【分析】根据坐标与图形变化,把三角形三个顶点的横坐标都减2,纵坐标没有变,就是把三角形向左平移2个单位,大小没有变,形状没有变.
【详解】解:∵将三角形三个顶点的横坐标都减2,纵坐标没有变,
∴所得三角形与原三角形的关系是:将原图向左平移两个单位.
故选A.
8. 对于函数y=x+6,下列结论错误的是( )
A. 函数图象与x轴交点坐标是(0,6) B. 函数值随自变量的增大而增大
C. 函数图象与x轴正方向成45°角 D. 函数图象没有第四象限
【正确答案】A
【分析】根据函数的性质,以及函数图象与坐标轴的交点的求法即可判断.
【详解】A.∵令y=0,则x=-6,∴函数y=x+6与x轴的交点坐标分别为(-6,0),故本选项错误;
B. ∵函数y=x+6中k=1>0,∴函数值随自变量增大而增大,故本选项正确;
C. ∵函数y=x+6与x、y轴的交点坐标分别为(-6,0),(0,6),
∴此函数与x轴所成角度的正切值==1,
∴函数图象与x轴正方向成45°角,故本选项正确;
D. ∵函数y=x+6中k=1>0,b=6>0,∴函数图象一、二、三象限,故本选项正确;故选A.
本题考查了函数的性质,在直线y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
9. 如图,点是矩形的,是上的点,沿折叠后,点恰好与点重合,若,则折痕的长为( )
A B. C. D. 6
【正确答案】A
【分析】先根据图形翻折变换的性质得出BC=OC,BE=OE,∠B=∠COE=90°,∠BCE=∠ACE,求出AC=2BC,求出∠BAC=30°,求出∠BCE=30°,解直角三角形求出CE即可.
【详解】解:∵△CEO是△CEB翻折而成,
∴BC=OC,BE=OE,∠B=∠COE=90°,∠BCE=∠ACE,
∴EO⊥AC,
∵O是矩形ABCD的,
∴OE是AC的垂直平分线,AC=2BC=2×3=6,
∴∠CAB=30°,
∴∠BCA=60°,
∴∠BCE=∠ACE=30°,
在Rt△BCE中,CE=,
故选:A.
本题考查了翻折变换,矩形的性质,直角三角形的性质,解直角三角形等知识点,能求出∠BAC=30°是解此题的关键.
10. 如图,正方形网格中的,若小方格边长为,则的形状为( )
A. 直角三角形 B. 锐角三角形
C. 钝角三角形 D. 以上答案都没有对
【正确答案】A
【分析】根据勾股定理求得△ABC各边的长,再利用勾股定理的逆定理进行判定,从而没有难得到其形状.
【详解】解:∵正方形小方格边长1,
∴BC=,
AC=,
AB=,
在△ABC中,
∵BC2+AC2=32+18=50,AB2=50,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
故选:A.
考查了勾股定理的逆定理,解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足a2+b2=c2,则三角形ABC是直角三角形.
二、填 空 题
11. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元方程组的解是______.
【正确答案】
【分析】由图可知:两个函数的交点坐标为(-4,-2);那么交点坐标同时满足两个函数的解析式,而所求的方程组正好是由两个函数的解析式所构成,因此两函数的交点坐标即为方程组的解.
【详解】解:函数y=ax+b和y=kx的图象交于点P(-4,-2),
即x=-4,y=-2同时满足两个函数的解析式.
所以关于x、y的二元方程组的解是,
故.
本题考查了函数与二元方程组的关系,方程组的解就是使方程组中两个方程同时成立的一对未知数的值,而这一对未知数的值也同时满足两个相应的函数式,因此方程组的解就是两个相应的函数图象的交点坐标.
12. 若样本1,2,3,x的平均数为5,又知样本1,2,3,x,y的平均数为6,那么样本1,2,3,x,y的方差是__________.
【正确答案】26
【详解】∵样本1,2,3,x的平均数为5,
∴1+2+3+x=5×4,
∴x=14,
∵样本1,2,3,x,y的平均数为6,
∴1+2+3+x+y=6×5,
∴x+y=24,
∴y=10,
∴样本的方差s2=[(1-6)2+(2-6)2+(3-6)2+(14-6)2+(10-6)2]÷5=26.
13. 已知O(0,0),A(-3,0),B(-1,-2),则△AOB的面积为__________.
【正确答案】3
【详解】∵A(﹣3,0),B(﹣1,﹣2),O为原点,
∴OA=3,OD⊥AO于点D,
∴S△AOB=OA•DB=×3×2=3.
故答案为3.
14. 小明家准备春节前举行80人的聚餐,需要去某餐馆订餐.据了解餐馆有10人坐和8人坐两种餐桌,要使所订的每个餐桌刚好坐满,则订餐共有______种.
【正确答案】3
【详解】试题分析:设10人桌x张,8人桌y张,根据题意得:10x+8y=80
∵x、y均为整数,
∴x=0,y=10或x=4,y=5或x=8,y=0共3种.
故答案是3.
考点:二元方程的应用.
15. 若函数与函数的图象关于X轴对称,且交点在X轴上,则这个函数的表达式为:______________________.
【正确答案】y=-x-1.
【详解】试题解析:∵两函数图象交于x轴,
∴0=x+1,
解得:x=-2,
∴0=-2k+b,
∵y=kx+b与y=x+1关于x轴对称,
∴b=-1,
∴k=-
∴y=-x-1.
考点:函数图象与几何变换.
16. 若直线y=ax+7函数y=4﹣3x和y=2x﹣1的交点,则a的值是_____.
【正确答案】-6
【详解】根据题意,得4﹣3x=2x﹣1,解得x=1,∴y=1.
把(1,1)代入y=ax+7,得a+7=1,解得a=﹣6.
故答案为﹣6.
17. 若关于x,y的二元方程组的解也是二元方程x+2y=8的解,则k的值为____.
【正确答案】2
【分析】据题意得知,二元方程组的解也是二元方程x+2y=8的解,也就是说,它们有共同的解,及它们是同一方程组的解,列出方程组解答即可.
【详解】根据题意,得
由(1)+(2),得
2x=4k即x=2k(4)
由(1)-(2),得
2y=2k即y=k(5)
将(4)、(5)代入(3),得
2k+2k=8,解得k=2.
本题考查了三元方程组的解,运用了加减消元法和代入消元法.通过“消元”,使其转化为二元方程(组)来解.
18. 如图(1),在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,ΔMNR的面积为y,若y关于x的函数图象如图(2)所示,则当x=9时,点R应运动到____.
【正确答案】Q处
【分析】由题意得当R在PN上运动时,面积没有断在增大,当到达点P时,面积开始没有变,到达Q后面积没有断减小.据此解答即可.
【详解】当R在PN上运动时,△MNR的面积没有断增大;
当R在QP上运动时,MN一定,高为PN没有变,此时面积没有变;
当R在QM上运动时,面积没有断减小.
∴当x=9时,点R应运动到高没有变的结束,即点Q处.故答案为Q处.
考查动点问题的函数的有关计算;根据所给图形得到矩形的边长是解决本题的关键.
三、解 答 题
19. (1)计算-.
(2)解方程组
【正确答案】(1)-. (2)
【分析】(1)先化简二次根式,然后进行二次根式的乘法和除法的运算即可;(2)用代入法求解即可.
【详解】(1)原式=-+3×2-;
(2)由3x-y=11,可得y=3x-11,再将y=3x-11代入2x+3y=0,得x=3,将x=3代入y=3x-11,得y=-2,所以原方程组的解为
本题考查了二次根式的混合运算及二元方程组的解法,解题的关键是掌握二次根式的运算法则及解二元方程组的步骤.
20. 若a,b为实数,且,求的值.
【正确答案】-3
【分析】根据二次根式的被开方数为非负数,得到相应的关系式求出a、b的值,然后代入求解.
【详解】因为a,b为实数,且a2-1≥0,1-a2≥0,所以a2-1=1-a2=0.
所以a=±1.又因为a+1≠0,所以a=1.代入原式,得b=.
所以=-3.
此题主要考查了二次根式的性质和意义,关键是利用被开方数为非负数的性质求出a、b的值.
21. 某校教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了统计,并绘制了下表
零花钱数额/元
5
10
15
20
学生人数
10
15
20
5
(1)求出这50名学生每人一周内的零花钱数额的平均数、众数和中位数;
(2)你认为(1)中的哪个数据代表这50名学生每人一周零花钱数额的一般水平较为合适?简要说明理由.
【正确答案】(1)平均数是12元;众数是15元;中位数是12.5元;(2)众数
【详解】试题分析:(1)根据平均数、中位数、众数的定义即可得到结果;
(2)根据(1)中求得的平均数、中位数、众数的值即可判断.
(1)平均数是(5×10+10×15+15×20+20×5)÷(10+15+20+5)=12元,
这组数据中人数至多是15元,故这组数据的众数是15元,
∵这组数据中的第25个数据是10元,第26个数据是15元
∴这组数据的中位数是(10+15)÷2=12.5元;
(2)用众数代表这50名学生一周零花钱数额的一般水平较为合适,因为15元出现次数至多,所以能代表一周零花钱的一般水平.
考点:本题考查的是平均数,中位数,众数
点评:解答本题的关键是熟记将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.
22. 直线PA是函数y=x+1的图象,直线PB是函数y=-2x+2的图象.
(1)求A,B,P三点的坐标;
(2)求四边形PQOB的面积;
【正确答案】(1)A(-1,0);B(1,0),P(,);(2).
【分析】(1)令函数y=x+1与函数y=﹣2x+2的y=0可分别求出A,B的坐标,再由可求出点P的坐标;
(2)设直线PB与y轴交于M点,根据四边形PQOB的面积=S△BOM﹣S△QPM即可求解.
【详解】(1)∵函数y=x+1的图象与x轴交于点A,∴A(﹣1,0),
函数y=﹣2x+2的图象与x轴交于点B,∴B(1,0),
由,解得,∴P.
(2)设直线PA与y轴交于点Q,则Q(0,1),直线PB与y轴交于点M,则M(0,2),
∴四边形PQOB的面积=S△BOM﹣S△QPM=×1×2﹣×1×
本题考查函数综合题型,难度一般,关键在于能够把四边形的面积分成两个三角形面积的差.
23. 小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.
(1)求s2与t之间的函数关系式;
(2)小明从家出发,多长时间在返回途中追上爸爸?这时他们距离家还有多远?
【正确答案】(1)s2=-96t+2400(2)小明从家出发,20min在返回途中追上爸爸,这时他们距离家还有480m
【分析】(1)首先由小明的爸爸以96m/min速度从邮局同一条道路步行回家,求得小明的爸爸用的时间,即可得点D的坐标,然后由E(0,2400),F(25,0),利用待定系数法即可求得答案;
(2)首先求得直线BC的解析式,然后求直线BC与EF的交点,即可求得答案.
【详解】解:(1)∵小明的爸爸以96m/min速度从邮局同一条道路步行回家,
∴小明的爸爸用的时间为:=25(min),
即OF=25,
如图:设s2与t之间的函数关系式为:s2=kt+b,
∵E(0,2400),F(25,0),
∴,
解得:,
∴s2与t之间的函数关系式为:s2=-96t+2400;
(2)如图:小明用了10分钟到邮局,
∴D点的坐标为(22,0),
设直线BD即s1与t之间的函数关系式为:s1=at+c(12≤t≤22),
∴
解得:,
∴s1与t之间函数关系式为:s1=-240t+5280(12≤t≤22),
当s1=s2时,小明在返回途中追上爸爸,
即-96t+2400=-240t+5280,
解得:t=20,
∴s1=s2=480,
∴小明从家出发,20min在返回途中追上爸爸,这时他们距离家还有480m.
此题考查了函数的实际应用.解题的关键是数形与方程思想的应用.注意小明的是折线,小明爸爸的是直线,抓住每部分的含义是关键.
24. 某大酒店客房部有三人间、双人间和单人间客房,收费数据如下表(例如三人间普通间客房每人每天收费50元).为吸引客源,在“十一黄金周”期间进行优惠大酬宾,凡团体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间、双人间普通客房,并且每个客房正好住满,一共花去住宿费1510元.
普通间(元/人/天)
豪华间(元/人/天)
贵宾间(元/人/天)
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500
(1)三人间、双人间普通客房各住了多少间?
(2)设三人间共住了x人,则双人间住了 人,一共花去住宿费用y元表示,写出y与x的函数关系式;
(3)如果你作为旅游团团长,你认为上面这种住宿方式是没有是费用至少?为什么?
【正确答案】(1)三人间、双人间普通客房各住了8间,13间.(2);(3)没有是.理由见解析
【分析】(1)分别设三人间和双人间为x,y,根据人数和钱数列方程组求解;
(2)根据收费列出表达式整理即可;
(3)利用(2)函数的性质,可得到y随着x的增大而减小,x为48,而题中安排方式x=24,故没有是
【详解】(1)设三人间普通客房住了x间,双人间普通客房住了y间,由题意可得,解得x=8,y=13
故三人间、双人间普通客房各住了8间,13间.
(2)设三人间共住了x人,则双人间住了50-x人,一共花去住宿费用y=[50x
+70(50-x)]=-10x+1750(0≤x<50)
(3)没有是,因为在函数中y随着x的增大而减小,因为x应该为3的倍数,所以x为48,故y取最小值时x=48,题中住宿方式三人间人数为24人,故没有是费用至少,费用至少为x=48时,y=1270元
本题主要考查函数简单应用,解题关键在于能够读懂题意,解出函数解析式.
2022-2023学年福建省泉州市八年级下册数学期末专项模拟模拟卷
(B卷)
一、选一选(每小题3分,共30分)
1. 下列命题:①两条平行直线被第三条直线所截,内错角相等;②两边分别相等且其中一组等边的对角也相等的两个三角形全等;③三角形的一个外角大于任何一个内角;④如果a2=b2,那么a=b.其中是真命题的有( )
A. 1个 B. 2个 C. 3个 D. 4个
2. 如图,在平面直角坐标系中,点在象限,若点关于轴的对称点在直线上,则的值为( )
A. -1 B. 1 C. 2 D. 3
3. 八年级1班生活委员小华去为班级购买两种单价分别为8元和10元盆栽,共有100元,若小华将100元恰好用完,共有几种购买( )
A. 2 B. 3 C. 4 D. 5
4. 如图,正方形ABCD的边长为2,动点P从C出发,在正方形的边上沿着C→B→A的方向运动(点P与A没有重合).设P的运动路程为x,则下列图象表示△ADP的面积y关于x的函数关系的是( )
A. B. C. D.
5. 如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )
A. 5 B. 3 C. 2 D. 3
6. 直角三角形两条直角边长分别是3,4,则该直角三角形的斜边长是( )
A. 2 B. 3 C. 4 D. 5
7. 在实数-,0,π,,1.41中,无理数有( )
A. 4个 B. 3个 C. 2个 D. 1个
8. 如图,下列条件没有能判断直线a∥b的是( )
A ∠1=∠4 B. ∠3=∠5 C. ∠2+∠5=180° D. ∠2+∠4=180°
9. 在某校冬季运动会上,有15名选手参加了200米预赛,取前八名进入决赛.已知参赛选手成绩各没有相同,某选手要想知道自己是否进入决赛,除了知道自己的成绩外,还需要了解全部成绩的( )
A. 平均数 B. 中位数 C. 众数 D. 方差
10. 如图所示,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为( )
A. (1,2) B. (2,2) C. (2,1) D. (1,1)
二、填 空 题(每小题3分,共15分)
11. 化简:______.
12. 如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的平分线FP相交于点P.若∠BEP=46°,则∠EPF=________°.
13. 若x,y满足+(2x+3y-13)2=0,则2x-y的值为________.
14. 平面直角坐标系内的一条直线同时满足下列两个条件:①没有第四象限;②与两条坐标轴所围成的三角形的面积为2,这条直线的解析式可以是_________(写出一个解析式即可).
15. 如图,在平面直角坐标系xOy中,三角板的直角顶点P的坐标为(2,2),一条直角边与x轴的正半轴交于点A,另一直角边与y轴交于点B,三角板绕点P在坐标平面内转动的过程中,当△POA为等腰三角形时,请写出所有满足条件的点B的坐标__________.
三、解 答 题(共55分)
16. 如图,小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处,判断△ABC的形状,并求出△ABC的面积.
17. (1)请写出一个二元方程组,使该方程组无解;
(2)利用函数图象分析(1)中方程组无解的原因.
18. 在下列网格中建立一个平面直角坐标系,在坐标系中描出与x轴的距离等于3与y轴的距离等于4的所有点,并写出这些点之间的轴对称关系.
19. 为了迎接郑州市第二届“杯”青少年校园足球超级联赛,某学校组织了体育知识竞赛.每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图,如图所示.
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.
20. 如图,已知直线CB∥OA,∠C=∠OAB=100°,点E、F线段BC上,满足∠FOB=∠AOB=α,OE平分∠COF.
(1)用含有α的代数式表示∠COE的度数;
(2)若沿水平方向向右平行移动AB,则∠OBC∶∠OFC的值是否发生变化?若变化,找出变化规律;若没有变,求其比值.
21. 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
(1)A、C两村间的距离为 km,a= ;
(2)求出图中点P坐标,并解释该点坐标所表示的实际意义;
(3)乙在行驶过程中,何时距甲10km?
22. 正方形OABC的边长为2,其中OA、OC分别在x轴和y轴上,如图①所示,直线lA、C两点.
(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标;
(2)如图②,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点.
①请求出|BE+DE|的最小值和此时点E的坐标;
②若将点D沿x轴翻折到x轴下方,直接写出|BE-DE|的值,并写出此时点E的坐标.
2022-2023学年福建省泉州市八年级下册数学期末专项模拟模拟卷
(B卷)
一、选一选(每小题3分,共30分)
1. 下列命题:①两条平行直线被第三条直线所截,内错角相等;②两边分别相等且其中一组等边的对角也相等的两个三角形全等;③三角形的一个外角大于任何一个内角;④如果a2=b2,那么a=b.其中是真命题的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【正确答案】A
【详解】分析是否为真命题,需要分析各命题的题设是否能推出结论,从而利用排除法得出答案.
解:①两条平行直线被第三条直线所截,内错角相等,正确;
②两边分别相等且其中一组等边的对角也相等的两个三角形全等,没有正确;
③三角形的一个外角大于任何一个内角,没有正确;
④如果a2=b2那么a=b,没有正确,例如(−1)2=12,但−1≠1;
所以真命题有1个.
故选A.
2. 如图,在平面直角坐标系中,点在象限,若点关于轴的对称点在直线上,则的值为( )
A. -1 B. 1 C. 2 D. 3
【正确答案】B
【分析】根据关于x轴的对称点的坐标特点可得B(2,−m),然后再把B点坐标代入y=−x+1可得m的值.
【详解】点A关于x轴的对称点B的坐标为:(2,﹣m),
将点B的坐标代入直线y=﹣x+1
得:﹣m=﹣2+1,
解得:m=1,
故选:B.
此题主要考查了关于x轴对称点的坐标,以及函数图象上点的坐标特点,关键是掌握凡是函数图象的点必能使解析式左右相等.
3. 八年级1班生活委员小华去为班级购买两种单价分别为8元和10元的盆栽,共有100元,若小华将100元恰好用完,共有几种购买( )
A. 2 B. 3 C. 4 D. 5
【正确答案】A
【详解】解:设购买单价为8元的盆栽x盆,购买单价为10元的盆栽y盆,
根据题意可得:8x+10y=100,
当x=10,y=2,
当x=5,y=6,
当x=0,y=10(没有合题意,舍去).
故符合题意的有2种,
故选:A.
此题主要考查了二元方程的应用,正确得出等量关系是解题关键.
4. 如图,正方形ABCD的边长为2,动点P从C出发,在正方形的边上沿着C→B→A的方向运动(点P与A没有重合).设P的运动路程为x,则下列图象表示△ADP的面积y关于x的函数关系的是( )
A. B. C. D.
【正确答案】C
【详解】解:当P点由C运动到B点时,即0≤x≤2时,y=×2×2=2;
当P点由B运动到A点时(点P与A没有重合),即2<x<4时,y=×2×(4-x)=4﹣x
∴y关于x的函数关系:
注:图象没有包含x=4这个点.
故选C.
点睛:本题考查了动点函数图象问题,在图象中应注意自变量的取值范围,注意分类讨论.
5. 如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为( )
A. 5 B. 3 C. 2 D. 3
【正确答案】C
【分析】过F点作FH⊥AD于H,在Rt△EHF中根据勾股定理即可求出EF的长.
【详解】解:如图所示,过F点作FH⊥AD于H,
设CF=x,则BF=8−x,
在Rt△ABF中,AB2+BF2=AF2,
∴16+(8−x)2=x2,
解得:x=5,
∴AF=CF=5,
∵AD//BC,
∴∠AEF=∠EFC,
又∵∠AFE=∠EFC,
∴∠AEF=∠AFE,
∴AE=AF=5,
∴EH=AE−AH=2,
∵FH=4,
∴EF2=42+22=20,
∴EF=;
故选C.
6. 直角三角形的两条直角边长分别是3,4,则该直角三角形的斜边长是( )
A. 2 B. 3 C. 4 D. 5
【正确答案】D
【详解】根据勾股定理即可得出答案.
解:∵直角三角形的两条直角边长分别是3,4,
∴该直角三角形的斜边长是:
故选D.
7. 在实数-,0,π,,1.41中,无理数有( )
A. 4个 B. 3个 C. 2个 D. 1个
【正确答案】C
【详解】根据无理数的定义:无限没有循环小数是无理数,对各数分别判断即可.
解:在实数-,0,π,,1.41中,无理数有π和,共2个.
故选C.
8. 如图,下列条件没有能判断直线a∥b的是( )
A. ∠1=∠4 B. ∠3=∠5 C. ∠2+∠5=180° D. ∠2+∠4=180°
【正确答案】D
【详解】A、能判断,∵∠1=∠4,∴a∥b,满足内错角相等,两直线平行,没有符合题意.
B、能判断,∵∠3=∠5,∴a∥b,满足同位角相等,两直线平行,没有符合题意.
C、能判断,∵∠2+∠5=180°,∴a∥b,满足同旁内角互补,两直线平行,没有符合题意.
D、没有能,符合题意.
故选D.
9. 在某校冬季运动会上,有15名选手参加了200米预赛,取前八名进入决赛.已知参赛选手成绩各没有相同,某选手要想知道自己是否进入决赛,除了知道自己的成绩外,还需要了解全部成绩的( )
A. 平均数 B. 中位数 C. 众数 D. 方差
【正确答案】B
【分析】一组数据从小到大(或从大到小)排列,中位数最中间一个数据或两个数据的平均数;15人成绩的中位数是第8名的成绩.参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
【详解】由于总共有15个人,且他们的分数互没有相同,第8的成绩是中位数,所以要判断是否进入前8名,只需要了解自己的成绩以及全部成绩的中位数.
故选B.
10. 如图所示,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为( )
A. (1,2) B. (2,2) C. (2,1) D. (1,1)
【正确答案】A
【分析】根据点E,F的坐标分别确定出坐标轴及原点的位置并建立平面直角坐标系,即可得出点G的坐标.
【详解】由点E坐标为(−2,1),点F坐标为(1,−1)可知左数第四条竖线是y轴,点E与点F中间的横线是x轴,其交点是原点,则点G的坐标为(1,2).
故选A.
本题主要考查点的坐标.根据已知条件正确建立平面直角坐标系是解题的关键.
二、填 空 题(每小题3分,共15分)
11. 化简:______.
【正确答案】3
【分析】根据算术平方根的概念求解即可.
【详解】解:因为32=9,
所以=3.
故答案为3.
此题主要考查了算术平方根的意义,关键是确定被开方数是哪个正数的平方.
12. 如图,AB∥CD,EF与AB,CD分别相交于点E,F,EP⊥EF,与∠EFD的平分线FP相交于点P.若∠BEP=46°,则∠EPF=________°.
【正确答案】68
【详解】由AB∥CD,根据两直线平行,同旁内角互补,即可得∠BEF+∠DFE=180°,又由EP⊥EF,∠EFD的平分线与EP相交于点P,∠BEP=46°,即可求得∠PFE的度数,然后根据三角形的内角和定理,即可求得∠EPF的度数.
解:∵AB∥CD,
∴∠BEF+∠DFE=180°,
∴EP⊥EF,
∴∠PEF=90°,
∵∠BEP=36°,
∴∠EFD=180°−90°−46°=44°,
∵∠EFD的平分线与EP相交于点P,
∴∠EFP =∠EFD=22°,
∴∠EPF=90°−∠EFP=68°.
故答案为68.
13. 若x,y满足+(2x+3y-13)2=0,则2x-y的值为________.
【正确答案】1
【详解】利用非负数的性质列出方程组,求出方程组的解得到x与y的值,代入原式计算即可得到结果.
解:∵+(2x+3y-13)2=0,
∴,
解得:,
则2x−y=4−3=1,
故答案为1.
14. 平面直角坐标系内的一条直线同时满足下列两个条件:①没有第四象限;②与两条坐标轴所围成的三角形的面积为2,这条直线的解析式可以是_________(写出一个解析式即可).
【正确答案】y=x+2,答案没有.
【详解】解:因为没有第四象限,k>0,b>0,与两条坐标轴所围成的三角形的面积为2,可得解析式为y=x+2,故答案为y=x+2(答案没有).
点睛:本题考查了待定系数法求解析式,关键是根据没有第四象限,与两条坐标轴所围成的三角形的面积为2解答.
15. 如图,在平面直角坐标系xOy中,三角板的直角顶点P的坐标为(2,2),一条直角边与x轴的正半轴交于点A,另一直角边与y轴交于点B,三角板绕点P在坐标平面内转动的过程中,当△POA为等腰三角形时,请写出所有满足条件的点B的坐标__________.
【正确答案】(0,2),(0,0),(0,4-2)
【详解】由P坐标为(2,2),可得∠AOP=45°,然后分别从OA=PA,OP=PA,OA=OP去分析求解即可求得答案.
解:∵P坐标为(2,2),
∴∠AOP=45°,
①如图1,若OA=PA,则∠AOP=∠OPA=45°,
∴∠OAP=90°,
即PA⊥x轴,
∵∠APB=90°,
∴PB⊥y轴,
∴点B的坐标为:(0,2);
②如图2,若OP=PA,则∠AOP=∠OAP=45°,
∴∠OPA=90°,
∵∠BPA=90°,
∴点B与点O重合,
∴点B的坐标为(0,0);
③如图3,若OA=OP,则∠OPA=∠OAP=(180°−∠AOP)=67.5°,
过点P作PC⊥y轴于点C,过点B作BD⊥OP于点D,
则PC∥OA,
∴∠OPC=∠AOP=45°,
∵∠APB=90°,
∴∠OPB=∠APB−∠OPA=225°,
∴∠OPB=∠CPB=22.5°,
∴BC=BD,
设OB=a,
则BD=BC=2−a,
∵∠BOP=45°,
在Rt△OBD中,BD=OB⋅sin45°,
即2−a=a,
解得:a=4-2.
综上可得:点B的坐标为:(0,2),(0,0),(0, 4-2).
故答案为(0,2),(0,0),(0, 4-2).
点睛:本题主要考查等腰三角形的性质.按题意画出所在符合条件的图形是解题的关键.
三、解 答 题(共55分)
16. 如图,小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点处,判断△ABC的形状,并求出△ABC的面积.
【正确答案】2
【详解】试题分析:利用勾股定理列式求出AB、BC、AC,再根据勾股定理逆定理判断△ABC的形状,根据三角形面积公式求出△ABC的面积.
试题解析:解:由勾股定理得,AB=,
BC=,
AC=,
∵AB2=BC2+AC2,
∴△ABC是直角三角形;
∴△ABC的面积为2
点睛:本题考查了勾股定理,勾股定理逆定理,三角形的面积,熟练掌握网格结构并准确找出对应点的位置是解题的关键.
17. (1)请写出一个二元方程组,使该方程组无解;
(2)利用函数图象分析(1)中方程组无解的原因.
【正确答案】(1)(答案没有);(2)见解析
【详解】根据函数与二元方程组的关系解答即可.
解:(1)方程组无解;
(2)两个二元方程对应的函数的图象如图所示,方程组无解的原因是两条直线没有交点.
18. 在下列网格中建立一个平面直角坐标系,在坐标系中描出与x轴的距离等于3与y轴的距离等于4的所有点,并写出这些点之间的轴对称关系.
【正确答案】见解析
【详解】根据题意立平面直角坐标系进而得出各点位置求出答案.
解:如图所示,
该点在象限时,其坐标为A(4,3);
该点在第二象限时,其坐标为B(-4,3);
该点在第三象限时,其坐标为C(-4,-3);
该点在第四象限时,其坐标为D(4,-3).
A与B关于y轴对称,
A与D关于x轴对称,
B与C关于x轴对称,
C与D关于y轴对称.
19. 为了迎接郑州市第二届“杯”青少年校园足球超级联赛,某学校组织了体育知识竞赛.每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图,如图所示.
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.
【正确答案】(1)见解析;(2)a=87.6,b=90,c=100;(3)见解析
【详解】(1)根据总人数为25人,求出等级C的人数,补全条形统计图即可;
(2)求出一班的平均分与中位数得到a与b的值,求出二班得众数得到c的值即可;
(3)分三种情况讨论,分别根据一班和二班的平均数和中位数、一班和二班的平均数和众数以及B级以上(包括B级)的人数进行分析,即可得出合理的答案.
解:(1)一班中C级的有25-6-12-5=2(人),补图如下:
(2)根据题意得:
a=(6×100+12×90+2×80+70×5)÷25=87.6;
中位数为90分,
二班众数为100分,
则a=87.6,b=90,c=100;
(3)①从平均数和中位数的角度,一班和二班平均数相等,一班的中位数大于二班的中位数,故一班成绩好于二班;②从平均数和众数的角度,一班和二班平均数相等,一班的众数小于二班的众数,故二班成绩好于一班;③从B级以上(包括B级)的人数的角度,一班有18人,二班有12人,故一班成绩好于二班.
20. 如图,已知直线CB∥OA,∠C=∠OAB=100°,点E、F线段BC上,满足∠FOB=∠AOB=α,OE平分∠COF.
(1)用含有α的代数式表示∠COE的度数;
(2)若沿水平方向向右平行移动AB,则∠OBC∶∠OFC的值是否发生变化?若变化,找出变化规律;若没有变,求其比值.
【正确答案】(1)∠COE=40°-α;(2)∠OBC∶∠OFC=1∶2.
【详解】(1)先根据平行线的性质得出∠AOC的度数与∠FBO=∠AOB,再由∠FOB=∠AOB,得出∠FBO=∠FOB即OB平分∠AOF,根据OE平分∠COF,可知∠EOB=∠EOF+∠FOB,故可得出结论;
(2)根据平行线的性质可得出∠OBC=∠BOA,∠OFC=∠FOA,从而得出答案.
解:(1)∵CB∥OA,
∴∠C+∠AOC=180°.
∵∠C=100°,
∴∠AOC=80°.
∵∠FOB=∠AOB=α,OE平分∠COF,
∴∠EOF=∠COF,∠FOB=∠FOA,
∴∠EOB=∠EOF+∠FOB,
=∠COF+∠FOA,
= (∠COF+∠FOA) ,
=∠AOC,
=40°. ,
∵OE平分∠COF,
∴∠COE=∠FOE=40°-α.
(2)∠OBC∶∠OFC的值没有发生改变.
∵BC∥OA,
∴∠FBO=∠AOB ,
∵∠BOF=∠AOB,
∴∠FBO=∠BOF,
∵∠OFC=∠FBO+∠FOB,
∴∠OFC=2∠OBC,
即∠OBC∶∠OFC=∠OBC∶2∠OBC=1∶2.
21. 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.设甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,请回答下列问题:
(1)A、C两村间的距离为 km,a= ;
(2)求出图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)乙在行驶过程中,何时距甲10km?
【正确答案】(1)A、C两村间的距离120km,a=2;
(2)P(1,60)表示1小时甲与乙相遇且距C村60km.
(3)当x=h,或x=h,或x=h乙距甲10km.
【分析】(1)、根据函数图象得出A、C之间的距离;
(2)、首先分别求出两条直线的函数解析式,然后求出a的值和点P的坐标;
(3)、本题分y1-y2=10,y2-y1=10以及甲走到C地,而乙距离C地10km这3种情况分别列出方程,求出x的值.
【详解】(1)、A、C两村间的距离120km,
a=120÷[(120−90)÷0.5]=2;
(2)、设y1=k1x+120,代入(0.5,90)解得y1=-60x+120, 把y=0代入得x=2 ∴a=2
设y2=k2x+90,代入(3,0)解得y2=-30x+90,
由-60x+120=-30x+90,解得x=1,则y1=y2=60,
∴P(1,60)
所以P(1,60)表示1小时甲与乙相遇且距C村60km.
(3)、当y1-y2=10,即-60x+120-(-30x+90)=10,解得x=,
当y2-y1=10,即-30x+90-(-60x+120)=10,解得x=,
当甲走到C地,而乙距离C地10km时,-30x+90=10,解得x=;
综上所知当x=h,或x=h,或x=h乙距甲10km.
考点:函数的应用.
22. 正方形OABC的边长为2,其中OA、OC分别在x轴和y轴上,如图①所示,直线lA、C两点.
(1)若点P是直线l上的一点,当△OPA的面积是3时,请求出点P的坐标;
(2)如图②,坐标系xOy内有一点D(-1,2),点E是直线l上的一个动点.
①请求出|BE+DE|的最小值和此时点E的坐标;
②若将点D沿x轴翻折到x轴下方,直接写出|BE-DE|值,并写出此时点E的坐标.
【正确答案】(1)P(1,3)或P (-5,-3);(2)①最小值为 ,E ;②值为,点E (2,4).
【详解】(1)如图1中,求出直线l的解析式为y=x+2.设点P的坐标为(m,m+2),由题意得×2×|m+2|=3,解方程即可;
(2)如图2中,连接OD交直线l于点E,则点E为所求,此时|BE+DE|=|OE+DE|=OD,OD即为值.求出直线OD的解析式,利用方程组求出等E坐标即可;
(3)如图3中,O与B关于直线l对称,所以BE=OE,|BE-DE|=|OE-DE|.由两边之差小于第三边知,当点O,D,E三点共线时,|OE-DE|的值,值为OD.求出直线OD的解析式,利用方程组求出交点E坐标即可.
解:(1)如图①,由题意知点A、点C的坐标分别为(-2,0)和(0,2).
设直线l的函数表达式y=kx+b(k≠0),
其点A(-2,0)和点C(0,2),代入得 ,
解得 ,
∴直线l的解析式为y=x+2.
设点P的坐标为(m,m+2),由题意得×2×|m+2|=3,
∴m=1或-5.
∴P1(1,3),P2 (-5,-3).
(2)①如图②,连接OD交直线l于点E,则点E为所求,
此时|BE+DE|=|OE+DE|=OD,OD即为最小值.
设OD所在直线为y=k1x(k1≠0),点D(-1,2),
∴k1=-2,
∴直线OD的解析式为y=-2x.
由,解得,
∴点E的坐标为.
又∵点D的坐标为(-1,2),
∴由勾股定理可得OD=.
即|BE+DE|的最小值为.
②如图③,∵O与B关于直线l对称,
∴BE=OE,
∴|BE-DE|=|OE-DE|.
由三角形的两边之差小于第三边知,当点O,D,E三点共线时,|OE-DE|的值,值为OD.
∵D(-1,-2),
∴直线OD的解析式为y=2x,OD= =.
由解得,
∴点E的坐标为(2,4).
∴|BE-DE|的值为,此时点E的坐标为(2,4).
点睛:本题是一道函数综合题.利用两直线相交建立方程组求解是解题的关键.
2022-2023学年福建省泉州市七年级下册数学期末专项提升模拟题(AB卷)含解析: 这是一份2022-2023学年福建省泉州市七年级下册数学期末专项提升模拟题(AB卷)含解析,共44页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。
2022-2023学年福建省泉州市七年级下册数学期末专项突破模拟题(AB卷)含解析: 这是一份2022-2023学年福建省泉州市七年级下册数学期末专项突破模拟题(AB卷)含解析,共51页。试卷主要包含了填 空 题,小器一容三斛;大器一,计算题,解 答 题等内容,欢迎下载使用。
2022-2023学年福建省泉州市七年级上册数学期末专项提升模拟卷(AB卷)含解析: 这是一份2022-2023学年福建省泉州市七年级上册数学期末专项提升模拟卷(AB卷)含解析,共41页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。












