






- 4.3.2对数的运算课件PPT 课件 0 次下载
- 4.4 第2课时对数函数图象及性质的应用课件PPT 课件 0 次下载
- 4.4 第3课时不同函数增长的差异课件PPT 课件 0 次下载
- 4.5.1函数的零点与方程的解课件PPT 课件 0 次下载
- 4.5.2用二分法求方程的近似解课件PPT 课件 0 次下载
人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.4 对数函数教学课件ppt
展开| 自 学 导 引 |
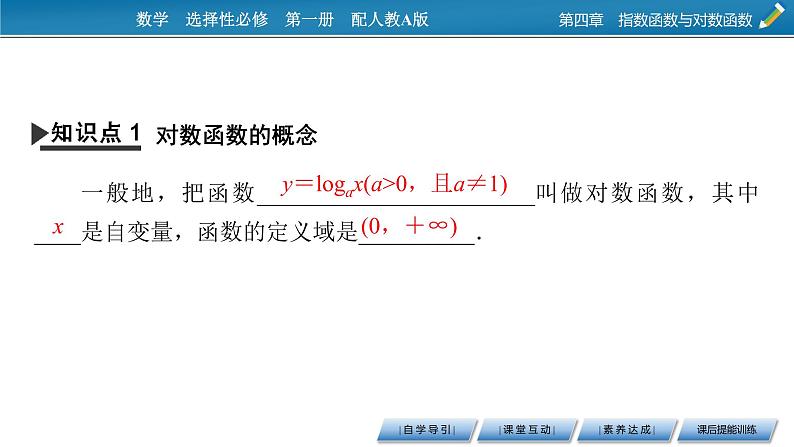
一般地,把函数________________________叫做对数函数,其中____是自变量,函数的定义域是__________.
y=lgax(a>0,且a≠1)
【答案】(1)× (2)× (3)×
【解析】(1)对数函数中自变量x在真数的位置上,且x>0,所以(1)错;(2)在解析式y=lgax中,lgax的系数必须是1,所以(2)错;(3)由对数式y=lg3(x+1)的真数x+1>0可得x>-1,所以函数的定义域为(-1,+∞),所以(3)错.
怎样可以快速画出对数函数y=lgax(a>0,且a≠1)的草图?
对数函数y=lgax(a>0,且a≠1),当a>1,x取何值时,y>0?x取何值时,y<0?当0
对数函数y=lgax(a>0,且a≠1)与__________________________互为反函数,它们的定义域与值域正好交换.
指数函数y=ax(a>0,且a≠1)
【预习自测】设函数f(x)=2x的反函数为g(x),若g(2x-3)>0,则x的取值范围是________.【答案】(2,+∞)【解析】易知f(x)=2x的反函数为y=lg2x,即g(x)=lg2x,g(2x-3)=lg2(2x-3)>0,所以2x-3>1,解得x>2.
| 课 堂 互 动 |
(1)下列函数表达式中,是对数函数的有( )①y=lgx2;②y=lgax(a∈R);③y=lg8x;④y=ln x;⑤y=lgx(x+2);⑥y=2lg4x;⑦y=lg2(x+1).A.1个B.2个C.3个D.4个(2)若对数函数f(x)的图象过点(4,-2),则f(8)=________.素养点睛:考查数学抽象的核心素养.【答案】(1)B (2)-3
题型1 对数函数的概念及应用
判断一个函数是对数函数的方法
1.下列函数是对数函数的是( )A.y=lga(2x)B.y=lg22xC.y=lg2x+1D.y=lg x【答案】B【解析】选项B中,2x>0恒成立,满足对数函数的概念.
题型2 对数型函数的定义域
求与对数函数有关的函数的定义域时应遵循的原则(1)分母不能为0.(2)根指数为偶数时,被开方数非负.(3)对数的真数大于0,底数大于0且不为1.
(1)函数y=lga(x+2)+1的图象过定点( )A.(1,2)B.(2,1)C.(-2,1)D.(-1,1)
题型3 对数函数的图象问题
(2)如图,曲线C1,C2,C3,C4分别对应函数y=lga1x,y=lga2x,y=lga3x,y=lga4x的图象,则( )A.a4>a3>1>a2>a1>0B.a3>a4>1>a1>a2>0C.a2>a1>1>a4>a3>0D.a1>a2>1>a3>a4>0(3)作函数y=|lg2(x+1)|+2的图象.素养点睛:考查直观想象和逻辑推理的核心素养.【答案】(1)D (2)A
【解析】(1)令x+2=1,即x=-1,得y=lga1+1=1,故函数y=lga(x+2)+1的图象过定点(-1,1).(2)作直线y=1,它与各曲线C1,C2,C3,C4的交点的横坐标就是各对数的底数,由此可判断出各底数的大小必有a4>a3>1>a2>a1>0.(3)解:第一步:作y=lg2x的图象,如图1所示.
第二步:将y=lg2x的图象沿x轴向左平移1个单位长度,得y=lg2(x+1)的图象,如图2所示.
第三步:将y=lg2(x+1)的图象在x轴下方的部分翻折到x轴上方,得y=|lg2(x+1)|的图象,如图3所示.第四步:将y=|lg2(x+1)|的图象沿y轴向上平移2个单位长度,即得到所求的函数图象,如图4所示.
1.对数函数图象过定点问题求函数y=m+lgaf(x)(a>0,且a≠1)的图象过定点时,只需令f(x)=1求出x,即得定点为(x,m).2.根据对数函数图象判断底数大小的方法作直线y=1与所给图象相交,交点的横坐标即为各个底数,依据在第一象限内,自左向右,图象对应的对数函数的底数逐渐变大,可比较底数的大小.
3.函数图象的变换规律:(1)一般地,函数y=f(x±a)+b(a,b为实数)的图象是由函数y=f(x)的图象沿x轴向左或向右平移,再沿y轴向上或向下平移得到的.(2)含有绝对值的函数的图象一般是经过对称变换得到的.
3.已知a>0且a≠1,函数y=lgax,y=ax,y=x+a在同一坐标系中的图象可能是( )
【答案】C【解析】若a>1,则y=lgax的图象上升且过点(1,0),y=ax的图象上升且过点(0,1),y=x+a在y轴的截距大于1,题中图象均不符;若0
1.判断一个函数是不是对数函数,关键是分析所给函数是否具有y=lgax(a>0,且a≠1)这种形式.2.在对数函数y=lgax中,底数a对其图象直接产生影响,学会以分类的观点认识和掌握对数函数的图象和性质.3.涉及对数函数定义域的问题,常从真数和底数两个角度分析.
1.(题型1)下列函数是对数函数的是( )A.y=lga(2x)B.y=lg22xC.y=lg2x+1D.y=lg x【答案】D【解析】选项A,B,C中的函数都不具有“y=lgax(a>0,且a≠1)”的形式,只有D选项符合.
5.(题型3)已知f(x)=lg3x.(1)作出函数f(x)的图象;(2)当0
数学必修 第一册第四章 指数函数与对数函数4.4 对数函数教课内容ppt课件: 这是一份数学必修 第一册第四章 指数函数与对数函数4.4 对数函数教课内容ppt课件,共42页。PPT课件主要包含了增函数,对数函数的单调性,减函数,预习自测,对数复合函数的单调性,答案A等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册4.4 对数函数评优课课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册4.4 对数函数评优课课件ppt
高中数学人教A版 (2019)必修 第一册4.4 对数函数教课内容课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册4.4 对数函数教课内容课件ppt,共37页。













