






- 6.2.1平行四边形的判定(1)课件+教案 课件 10 次下载
- 6.2.2平行四边形的判定(2)课件+教案 课件 9 次下载
- 6.2.3平行四边形性质与判定的综合应用 课件+教案 课件 8 次下载
- 6.3 三角形的中位线 课件+教案 课件 10 次下载
- 6.4 多边形的内角和与外角和 课件+教案 课件 9 次下载
第六章 平行四边形 章末复习 课件+教案
展开章末复习
【知识与技能】
1.能够熟练掌握平行四边形的判定和性质定理,并能够应用数学符号语言表述证明过程.
2.掌握三角形中位线的定义和性质,明确三角形中位线与中线的不同并能运用它进行有关的论证和计算.
3.掌握多边形内角和、外角和定理,进一步了解转化的数学思想.
4.会熟练应用所学定理进行证明.
【过程与方法】
通过讨论交流,进一步发展学生的合作交流意识.
【情感态度】
体会证明中所运用的归类、类比、转化等数学思想,通过复习课对证明的必要性有进一步的认识.
【教学重点】
熟练应用所学定理进行证明.
【教学难点】
熟练应用所学定理进行证明.
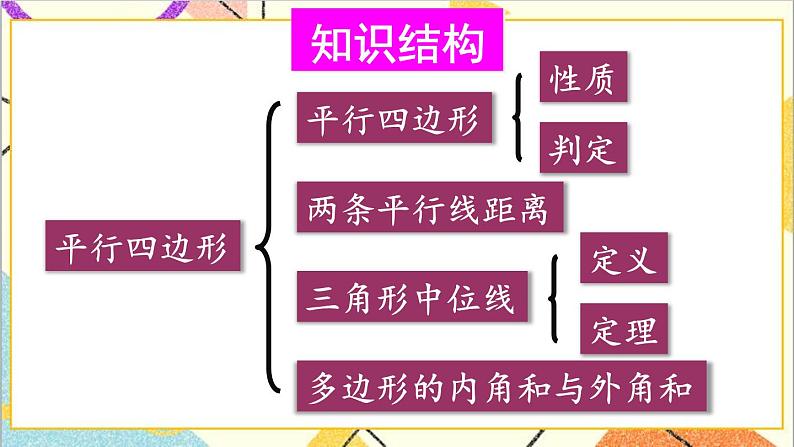
一.知识结构
【教学说明】引导学生回顾本章知识点,使学生系统地了解本章知识及它们之间的关系.
二.释疑解惑,加深理解
1.两组对边分别平行的四边形是平行四边形.
2.平行四边形的性质(边,角,对角线,对称性)
(1)边的性质:平行四边形的对边相等;平行四边形的对边平行;
(2)角的性质:平行四边形的对角相等 ;
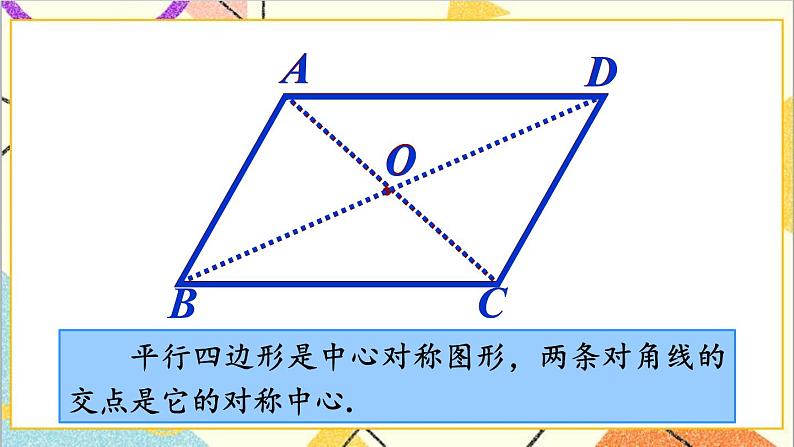
(3)对角线的性质:平行四边形的对角线互相平分;
(4)平行四边形是中心对称图形 .
3.平行四边形的判定.
(1)两组对边分别平行的四边形是平行四边形(定义);
(2)两组对边分别相等的四边形是平行四边形 ;
(3) 对角线互相平分的四边形是平行四边形 ;
(4)一组对边平行且相等的四边形是平行四边形;
(5)两组对角分别相等的四边形是平行四边形 .
4.两条平行线间的距离的定义.
若两条直线互相平行,则其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离,实际上平行线间的距离处处相等.
5.三角形的中位线 .
(1)三角形中位线的定义:连接三角形两边中点的线段叫做三角形的中位线 ;
(2)三角形中位线定理:三角形的中位线平行于三角线的第三边,且等于第三边的一半.
6.多边形的内角与外角和 .
(1)多边形:在平面内,由若干条不在同一条直线上的线段首尾顺次相连组成的封闭图形叫做多边形 ;
(2)n边形的内角和是(n-2)·180°;
(3)多边形的外角和等于360°.
【教学说明】通过课前热身练习,学生对知识进行回忆,进一步体会平行四边形的性质、判定, 概念再现,知识梳理.
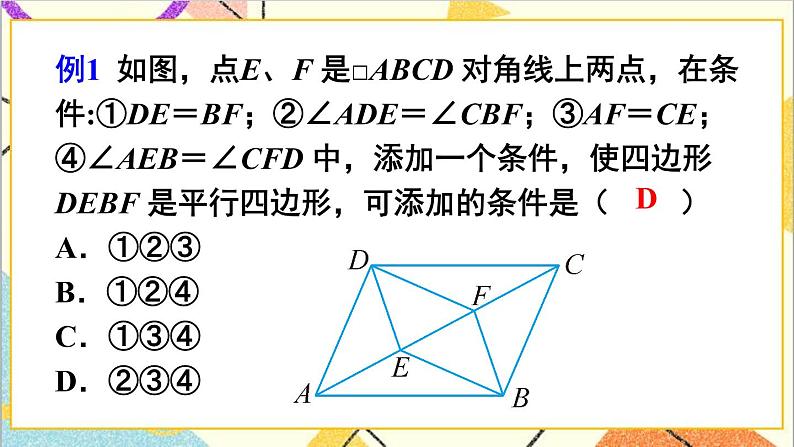
三.典例精析,复习新知
1.在四边形ABCD中,若AB=CD,再添加一个条件为_______________,就可以判定四边形ABCD为平行四边形.
答案:本题为开放式题目,只需添上一组能使四边形ABCD成平行四边形的条件即可,例AB∥CD.
2.已知E.F.G.H分别为□ABCD各边的中点,则四边形EFGH为_______.
答案:平行四边形.
3.下列结论正确的是( )
A.对角线相等且一组对角相等的四边形是平行四边形
B.一边长为5cm,两条对角线长分别是4cm和6cm的四边形是平行四边形
C.一组对边平行且一组对角相等的四边形是平行四边形
D.对角线相等的四边形是平行四边形
答案:C.
4.如图,在平行四边形ABCD中,EF∥AB,GH∥AD,EF与GH交于点O,则该图中的平行四边形的个数共有( )
A.7个 B.8个 C.9个 D.11个
答案:C.
5.已知如图直线m∥n,A.B为直线n上两点,C.D为直线m上两点,BC与AD交于点O,则图中面积相等的三角形有( )
A.1对 B.2对 C.3对 D.4对
答案:C.
6.若一个多边形内角和为1800°,求该多边形的边数.
解:设这个多边形的边数为n,则:
(n-2)×180°=1800°
n=12
即该多边形为十二边形
7.如图所示,在四边形ABCD中,DC∥AB,以AD,AC为边作□ACED,延长DC交EB于F,求证:EF=FB.
证明:过点B作BG∥AD,交DC的延长线于G,连接EG.
∵DC∥AB,∴ABGD是平行四边形,
∴BGAD.
在□ACED中,ADCE,∴CEBG.
∴四边形BCEG为平行四边形,∴EF=FB.
【教学说明】通过上面的解题分析,再对整个学习过程进行总结,能够促进理解,提高认识水平,从而促进数学观点的形成和发展,更好地进行知识建构,实现良性循环.
四.复习训练,巩固提高
1.多边形的内角和与某一个外角的度数总和为1350°,求该多边形的边数.
分析:该外角的大小范围应该是0°<x<180°
由此可得到该多边形内角和范围应该是
1170°<1350°-x<1350°,
而1350°-x=(n-2)·180°
解1:设该多边形边数为n,这个外角为x
则(n-2)·180°+x=1350°
∴
因为n为整数,所以必为整数.即:90°-x必为180°的倍数.
又因为0°<x<180°,所以x=90°,∴n=9.
解2:设该多边形边数为n,这个外角为x.
(n-2)·180°+x=1350°
0°<x<180°
∴1170°<1350°-x<1350°
∴1170°<(n-2)·180°<1350°
又∵n为整数,∴n=9.
则该多边形为九边形.
2.如图,在四边形ABCD中,点E是线段AD上的任意一点(E与A,D不重合),G,F,H分别是BE,BC,CE的中点.请证明四边形EGFH是平行四边形.
分析:(1)根据三角形中位线定理得GF∥EC, GF=EC=EH,一组对边平行且相等的四边形是平行四边形,所以EGFH是平行四边形.
证明:(1)在△BEC中,∵G,F分别是BE,BC的中点,
∴GF∥EC且GF=EC .
又∵H是EC的中点,EH=EC,
∴GF∥EH且GF=EH .
∴四边形EGFH是平行四边形.
3.如图,分别以△ABC的三边为边长,在BC的同侧作等边三角形ABD,等边三角形BCE,等边三角形ACF,连接DE,EF.求证:四边形ADEF是平行四边形.
解析:先证△EDB≌△CFE,
可得BD=EF,ED=CF.
∵BD=DA,CF=AF,
∴ED=AF,EF=DA,
∴四边形ADEF是平行四边形.
4.如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD于E,EF∥BC交AC于F,那么AE与CF相等吗?请验证你的结论.
解:AE=CF.
理由:过E作EG∥CF交BC于G,
∴∠3=∠C.
∵∠BAC=90°,AD⊥BC,
∴∠ABC+∠C=90°,∠ABD+∠BAD=90°.
∴∠C=∠BAD,∴∠3=∠BAD.
又∵∠1=∠2,BE=BE,
∴△ABE≌△GBE(AAS),∴AE=GE.
∵EF∥BC,EG∥CF,
∴四边形EGCF是平行四边形,∴GE=CF,
∴AE=CF.
【教学说明】这些训练题有一定的难度,应对学生分层教学.
五.师生互动,课堂小结
通过本节课的复习,你取得了哪些经验?(学生总结,老师补充)
布置作业:教材“复习题”中第3、5、6、9、11、13、14题.
本节复习课,我是先引导学生复习本章知识点.采用讨论、提问的方式进行教学,学生的积极性比较高,大部分学生都能掌握平行四边形的有关概念、性质定理、判定定理、多边形的内角和公式、外角和公式.通过知识点的回顾,学生对本章知识作了个系统的了解和整理.接着是例题讲解,这些例题都是基础知识,比较简单,可以先让学生独立完成,简答题可让个别学生上台板演,教师注重学生的板书过程,适当的作强调、更正.再是学生练习,这组练习题的难度较大,应采用分组教学,教师适当的提示、引导,使优生得到更好的锻炼、提高.









