北师大版（2019）高中数学必修第一册2-3函数的单调性教案

这是一份北师大版（2019）高中数学必修第一册2-3函数的单调性教案

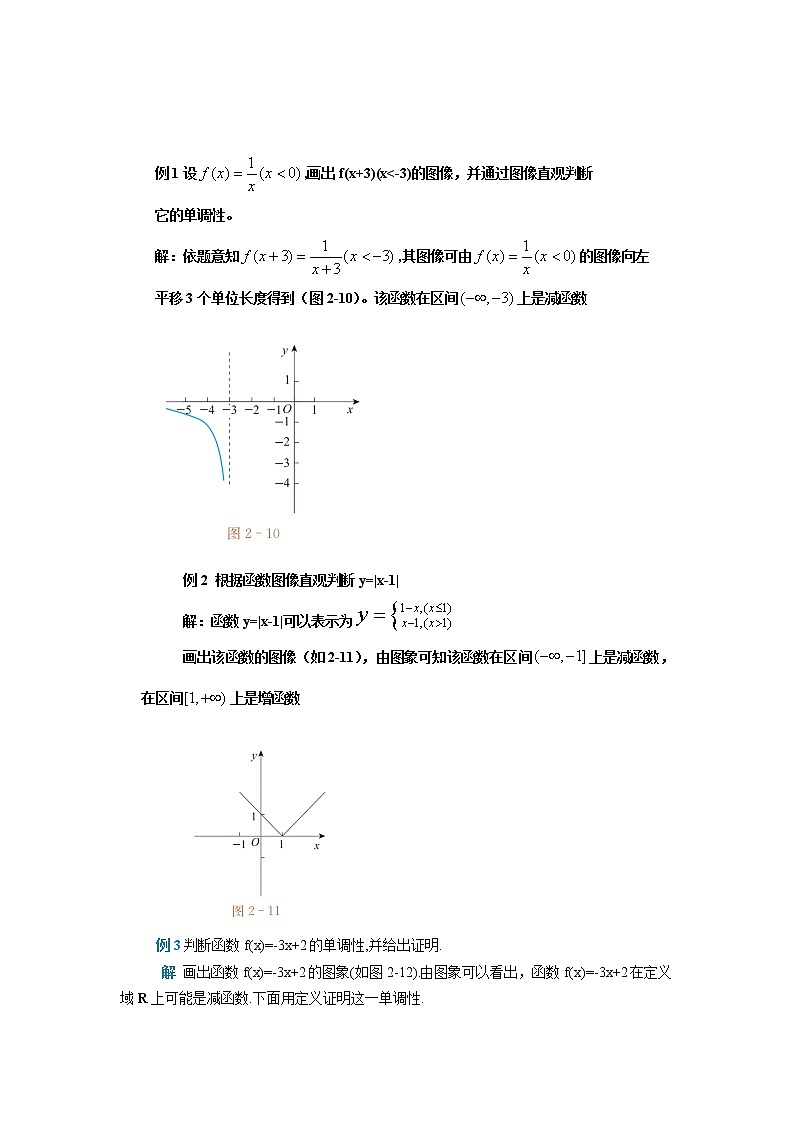
第 二 章 函 数第2.3节　函数的单调性教学设计本小节是函数性质之一单调性，揭示了函数图像的趋势，表示了自变量和因变量之间的关系，是数形结合数学思想的基础，与函数的奇偶性呈并列的关系，他俩从不同侧面研究函数性质。在函数性质中具有举足轻重的地位。本节利用图像观察推导单调性判断方法，该方法再次体现了数形结合的主要思想。教学目标1、理解函数单调性的概念，会根据函数的图像判断函数的单调性； 2、能够根据函数单调性的定义证明函数在某一区间上的单调性。二. 核心素养1. 数学抽象：函数在区间上单调性概念的概述2. 逻辑推理:本节课的教学，使学生能理性的描述生活中的增长、递减的现象；通过生活实例感受函数单调性的意义，培养学生的识图能力和数形语言转化的能力。3. 数学运算：判断函数的单调性及证明4. 直观想象：通过对函数单调性定义的探究，渗透数形结合的数学思想方法，培养学生的观察、归纳、抽象思维能力。5. 数学建模:本节课的教学，启发学生养成细心观察，认真分析，严谨论证的良好习惯；通过问题链的引入，激发学生学习数学的兴趣，学生通过积极参与教学活动，获得成功的体验，锻炼克服困难的意志，建立学习数学的自信心。 教学重点函数单调性的概念、判断及证明教学难点归纳抽象函数单调性的定义以及根据定义证明函数的单调性PPT1.知识引入函数是刻画变量关系的.研究函数y=f(x)时最关心的问题是：当自变量x变化时，函数值f(x)随之怎样变化.我们知道，一次函数y = kx+b,当k<0时，在R上y值随x值的增大而减小；当k>0时，在R上y值随x值的增大而增大.一元二次函数和反比例函数也有类似的性质.可见，用增大或减小来刻画函数在一个区间的变化是非常重要的.如下图分析：思考： 图2-9中，怎样用数学的符号语言表达函数值f(x)在区间[-6, -5]上隨x值的增大而增大呢？图2-9是函数f(x)的图象,直观上可以看出，对于区间[-6, -5],[-2,1],[3,4.5]，[7,8],每个区间上函数值f(x)都随x值的增大而增大；对于区间 [-5 , -2] , [1,3] , [ 4.5,7] , [ 8,9],每个区间上函数值f (x)都随x值的增大而减小.2.函数的单调性定义概述一般地，在函数y=f（x）定义域内的一个区间A上,如果对于任意的,当x1f(x2),那么就称函数y=f(x)在区间A上是减函数或递减的.如果函数y=f(x)在区间A上是增函数或减函数,那么就称函数y=f(x)在区间A上是单调函数，或称函数y=f(x)在区间A上具有单调性.此时，区间A为函数y=f(x)的单调区间.备注：1.概念中应该注意问题：任意的（不能写成“存在”）2.在单调区间上，增函数的图象是上升的，减函数的图象是下降的.在函数y=f（x）定义域内的一个区间A上,如果对于任意的且若[f(x1)-f(x2)](x1-x2)>0或，则函数称函数y=f(x)在区间A上是增函数或递增若[f(x1)-f(x2)](x1-x2)<0或，则函数称函数y=f(x)在区间A上是减函数或递减知识扩充： 例1设,画出f(x+3)(x<-3)的图像，并通过图像直观判断它的单调性。解：依题意知,其图像可由的图像向左平移3个单位长度得到（图2-10）。该函数在区间上是减函数例2 根据函数图像直观判断y=|x-1|解：函数y=|x-1|可以表示为画出该函数的图像（如2-11），由图象可知该函数在区间上是减函数，在区间上是增函数例3判断函数f(x)=-3x+2的单调性,并给出证明. 解 画出函数f(x)=-3x+2的图象(如图2-12).由图象可以看出，函数f(x)=-3x+2在定义域R上可能是减函数.下面用定义证明这一单调性.任取,且x10即：f(x1)>f(x2)函数f(x)=-3x+2在定义域R上是减函数.例4判断函数的单调性,并给出证明.解 画出函数的图象(如图2-13).由图象可以看出，函数在定义域 上可能是增函数.在定义域上任取x1 , x2,且x1