数学必修 第一册第四章 对数运算和对数函数5 信息技术支持的函数研究学案及答案

§4　指数函数、幂函数、对数函数增长的比较

*§5　信息技术支持的函数研究

课前篇·自主梳理知识

【主题】　函数模型的比较

三种函数增长的比较

(1)在(0，＋∞)上，指数函数y＝ax(a>1)、对数函数y＝logbx(b>1)、幂函数y＝xc(x>0，c>0)都是________函数，而且当x的值趋近于正无穷大时，y的值都是趋近于正无穷大的．但它们的函数值的增长速度不同，且不在同一个“档次”上．

(2)在(0，＋∞)上，随着x的增大，y＝ax(a>1)增长速度________，会超过并远远大于y＝xc(c>0)的增长速度；而y＝logbx(b>1)的增长速度则会________．

(3)存在一个x0，使得当x>x0时，有________．

答案：

(1)增　(2)越来越快　越来越慢　(3)logbx0<x<ax0

[自我检测]

1．思维辨析(对的打“√”，错的打“”)

(1)函数y＝x2比y＝2x增长的速度更快些．(　　)

(2)当a>1，n>0时，在区间(0，＋∞)上，对任意的x，总有logax<xn<ax成立．(　　)

(3)对于任意的x>0，都有2x>log2x.(　　)

答案：

(1)　解析：函数y＝x2和y＝2x增长的速度的快慢交替出现．

(2)　解析：当a>1，n>0时，当x足够大时，logax<xn<ax成立．

(3)√　解析：对于任意的x>0，函数2x的图象总是在函数log2x的图象的上方．

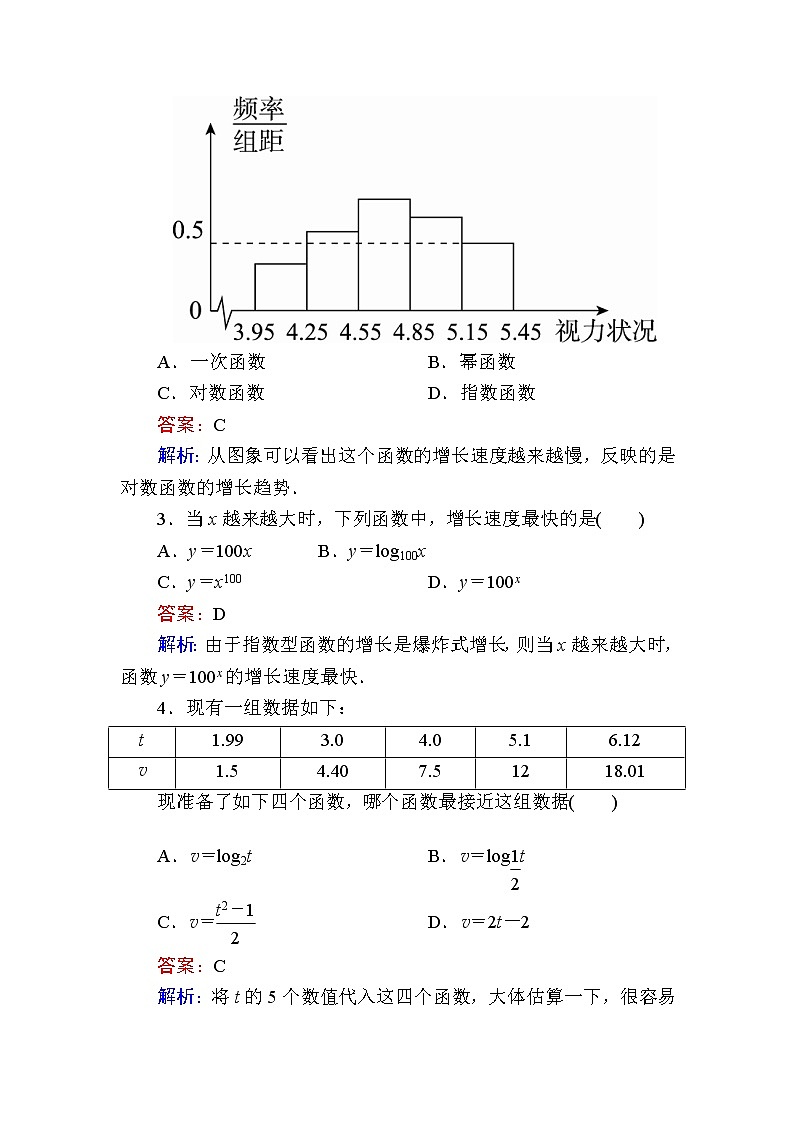
2．如图反映的是下列哪类函数的增长趋势(　　)

A．一次函数　　　 B．幂函数

C．对数函数        D．指数函数

答案：C　

解析：从图象可以看出这个函数的增长速度越来越慢，反映的是对数函数的增长趋势．

3．当x越来越大时，下列函数中，增长速度最快的是(　　)

A．y＝100x       B．y＝log100x

C．y＝x100        D．y＝100x

答案：D　

解析：由于指数型函数的增长是爆炸式增长，则当x越来越大时，函数y＝100x的增长速度最快．

4．现有一组数据如下：

现准备了如下四个函数，哪个函数最接近这组数据(　　)

A．v＝log2t        B．v＝logt

C．v＝        D．v＝2t－2

答案：C　

解析：将t的5个数值代入这四个函数，大体估算一下，很容易发现v＝的函数比较接近表中v的5个数值．

课堂篇·重难要点突破

研习1　函数模型的增长差异

[典例1]　研究函数y＝0.5ex－2，y＝ln(x＋1)，y＝x2－1在[0，＋∞)上的增长情况．

解：分别在同一个坐标系中画出三个函数的图象，如图所示，

从图象上可以看出函数y＝0.5ex－2的图象首先超过了函数y＝ln(x＋1)的图象，然后又超过了函数y＝x2－1的图象，即存在一个x0满足0.5ex0－2＝x－1，当x>x0时，ln(x＋1)<x2－1<0.5ex－2.

三种函数模型的表达形式及其增长特点

(1)指数函数模型：能用指数型函数f(x)＝abx＋c(a，b，c为常数，a>0，b>1)表达的函数模型，其增长特点是随着自变量x的增大，函数值增大的速度越来越快，常称之为“指数爆炸”．

(2)对数函数模型：能用对数型函数f(x)＝mlogax＋n(m，n，a为常数，m≠0，x>0，a>1)表达的函数模型，其增长的特点是开始阶段增长得较快，但随着x的逐渐增大，其函数值变化得越来越慢，常称之为“蜗牛式增长”．

(3)幂函数模型：能用幂型函数f(x)＝axα＋b(a，b，α为常数，a≠0，α≠1)表达的函数模型，其增长情况由a和α的取值确定，常见的有二次函数模型和反比例函数模型．

[练习1]若x∈(0,1)，试分析三个函数模型y＝2x，y＝x，y＝lg  x的增长差异，用“>”把它们的取值大小关系连接起来为________．

答案：2x>x>lg x　

解析：当x∈(0,1)时，2x>1，1>x>0，lg x<0，所以2x>x>lg x.

研习2  指数函数、对数函数、幂函数的图象

[典例2]　四个函数在第一象限中的图象如图所示，a，b，c，d所表示的函数可能是(　　)

A．a：y＝2x　b：y＝x2　c：y＝　d：y＝2－x

B．a：y＝x2　b：y＝2x　c：y＝2－x　d：y＝

C．a：y＝x2　b：y＝2x　c：y＝　d：y＝2－x

D．a：y＝2x　b：y＝x2　c：y＝2－x　d：y＝

答案：C　

解析：根据幂函数、指数函数、对数函数的性质和图象的特点，a，c对应的函数分别是幂指数大于1和幂指数大于0且小于1的幂函数，且b，d对应的函数分别为底数大于1和底数大于0且小于1的指数函数．

注意三种函数特有的性质．指数函数过点(0,1)．对数函数过点(1,0)．幂函数，当n>0时，过点(0,0)，(1,1)；当n<0时，不过点(0,0)，过点(1,1)．还要注意结合单调性进行判断．

[练习2]函数f(x)＝的图象和函数g(x)＝log2x的图象的交点个数是(　　)

A．4　　　　B．3　　　　C．2　　　　D．1

答案：B　

解析：在同一坐标系中画出函数f(x)＝和g(x)＝log2x的图象，如图所示，由图象知，有3个交点．

研习3  　比较大小

[典例3]　已知f(x)＝ax，g(x)＝x，h(x)＝logax，其中a满足loga(1－a2)>0，那么当x>1时，f(x)，g(x)，h(x)的大小关系是什么？

解：∵1－a2<1，loga(1－a2)>0，

∴0<a<1.

∴函数f(x)＝ax与h(x)＝logax在(1，＋∞)上均为减函数，

∴当x∈(1，＋∞)时，0<ax<1，logax<0.

又∵>0，

∴g(x)＝x在(1，＋∞)上是增函数．

∴对任意x∈(1，＋∞)均有g(x)>g(1)＝1.

综上可知，当x>1时，

h(x)＝logax<0<f(x)＝ax<1<g(x)＝x，

即h(x)<f(x)<g(x)．

(1)函数f(x)＝ax，h(x)＝logax的单调性取决于a与1的大小，y＝xn中n>0时，y＝xn在(0，＋∞)上是增函数．

(2)增长性快慢的比较：y＝ax(a>1)增长较快，有“指数爆炸”之说，y＝xn较y＝logax(a>1)增长要快，但要注意需x达到一定程度．

(3)函数值的分析：要熟练掌握f(x)＝ax，h(x)＝logax中的函数值特征，y＝xn过定点(1,1)，在第一象限一定有图象．

[练习3]若x∈(e－1,1)，a＝ln x，b＝2ln x，c＝(ln x)3，则(　　)

A．a<b<c　　　　 B．c<a<b

C．b<a<c        D．b<c<a

答案：C　

解析：∵<x<1，∴－1<ln x<0.

令t＝ln x，则－1<t<0，

∴a－b＝－t>0，∴a>b.

∵c－a＝t3－t＝t(t2－1)＝t(t＋1)(t－1)，

又∵－1<t<0，

∴0<t＋1<1，－2<t－1<－1，

∴c－a>0，∴c>a>b.

故选C．

研习4  几种函数模型增长比较的应用

[典例4]　(1)(2020·北京高一检测)某商场2018年一月份到十二月份销售额呈现先下降后上升的趋势，现有三种函数模型：

①f(x)＝p·qx(q>0，且q≠1)；

②f(x)＝logpx＋q(p>0，且p≠1)；

③f(x)＝x2＋px＋q.

能较准确反映商场月销售额f(x)与月份x关系的函数模型为________(填写相应函数的序号)，若所选函数满足f(1)＝10，f(3)＝2，则f(x)＝________.

(2)某企业拟共用10万元投资甲、乙两种商品，已知各投入x万元时，甲、乙两种商品可分别获得y1万元，y2万元的利润，利润曲线P1：y1＝axn，P2：y2＝bx＋c如图所示．

①求函数y1，y2的解析式；

②为使投资获得最大利润，应怎样分配投资额？

[审题路线图]分析函数的单调性、由图象中的点确定解析式⇒下结论．

(1)答案：③  x2－8x＋17，x∈{1,2，…，12}

(2)解：①由题图知P1：y1＝axn过点，.

所以所以

所以y1＝x，x∈[0，＋∞)．

P2：y2＝bx＋c过点(0,0)，(4,1)，所以

所以所以y2＝x，x∈[0，＋∞)．

②设用x万元投资甲商品，那么投资乙商品为(10－x)万元，总利润为y万元．

则y＝＋(10－x)＝－x＋＋

＝－2＋(0≤x≤10)．

当且仅当＝，即x＝＝6.25时，ymax＝.

此时投资乙商品为10－x＝10－6.25＝3.75.

故用6.25万元投资甲商品，3.75万元投资乙商品，才能获得最大利润．

[延伸探究]　(1)本例(1)中若商场销售额下降，其他条件不变，应选择哪个函数模型？试求出此函数解析式．

(2)本例(1)条件不变，试分析此商场哪个月销售额最小？

(1)解：选择对数型函数f(x)＝logpx＋q(p>0，且p≠1)．

因为f(1)＝10，f(3)＝2，所以

解得

f(x)＝－8log3x＋10，

当4≤x≤12，且x∈N＋时，f(x)<0，不合题意．

选择指数型函数f(x)＝p·qx(q>0，且q≠1)，

因为f(1)＝10，f(3)＝2，

所以解得

所以f(x)＝10·x＝2×5，x∈{1,2，3，…，12}，

故应选择指数型函数模型，函数解析式为f(x)＝2×5，x∈{1,2,3，…，12}．

(2)解：因为f(x)＝x2－8x＋17＝(x－4)2＋1，

所以f(x)min＝f(4)＝1，所以此商场4月销售额最小．

实际问题中对几种增长模型的选择技巧

(1)指数函数增长模型适合于描述增长速度快的变化规律．

(2)对数函数增长模型比较适合于描述增长速度平缓的变化规律．

(3)幂函数增长模型介于上述两者之间，适合一般增长的变化规律．

[练习4]函数f(x)＝lg x，g(x)＝0.3x－1的图象如图．

(1)指出C1，C2分别对应图中哪一个函数；

(2)比较两函数的增长差异．(以两图象交点为分界点，对f(x)，g(x)的大小进行比较)

解：(1)由函数图象特征及变化趋势，知

曲线C1对应的函数为g(x)＝0.3x－1，

曲线C2对应的函数为f(x)＝lg x.

(2)当x∈(0，x1)时，g(x)>f(x)；

当x∈(x1，x2)时，g(x)<f(x)；

当x∈(x2，＋∞)时，g(x)>f(x)．

函数g(x)呈直线增长，函数f(x)随着x的逐渐增大，其函数值变化得越来越慢，为“蜗牛式”增长．

课后篇·演练提升方案1.某县房价(均价)经过6年时间从1 200元/平方米增加到了4 800元/平方米，则这6年间平均每年的增长率是 (　　)

A．－1    B．＋1

C．50%    D．

答案：A　

解析：设年平均增长率为x，则1 200(1＋x)6＝4 800，解得x＝－1.

2．洗衣服时，若每次能洗去污垢的，要使存留的污垢不超过1%，则至少要洗的次数是  (　　)

A．3        B．4

C．5        D．6

答案：B　

解析：设要洗x次，则x≤，

∴x≥≈3.32，因此至少要洗4次，故选B．

3．某动物数量y(只)与时间x(年)的关系为y＝alog3(x＋1)，设第二年有100只，则到第8年该动物的数量发展到(　　)

A．200只        B．400只

C．500只        D．600只

答案：A　

解析：由已知第二年有100只，得100＝alog33，

∴a＝100，将a＝100，x＝8代入，得

y＝100×log3(8＋1)＝200.故选A．

4．某公司的股票今天的指数是2，以后每天的指数都比前一天的指数增长0.2%，则100天内(包括第100天)，这家公司的股票的指数y随经过天数x变化的函数关系式为________．

答案：y＝2(1＋0.2%)x(x∈N＋，且x≤100)

解析：设这家公司的股票的指数随经过天数x增加到y，由题意得y＝2(1＋0.2%)x(x∈N＋，且x≤100)．

5．从2013年起，在20年内我国力争使全国工农业生产总产值翻两番，如果每年的增长率是8%，则达到翻两番目标的最少年数为________．(log10.84≈18.01)

答案：19　

解析：设2013年我国工农业总产值为a，达到翻两番目标需n年，则翻两番后变为4a，由a(1＋8%)n≥4a，得1.08n≥4(n∈N＋)，

∴n≥log1.084≈18.01.

又∵n∈N＋，∴n≥19.