必修 第一册3.2 频率分布直方图课时作业

这是一份必修 第一册3.2 频率分布直方图课时作业

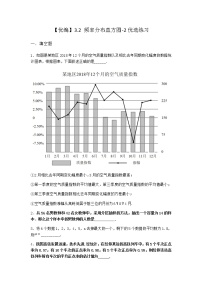
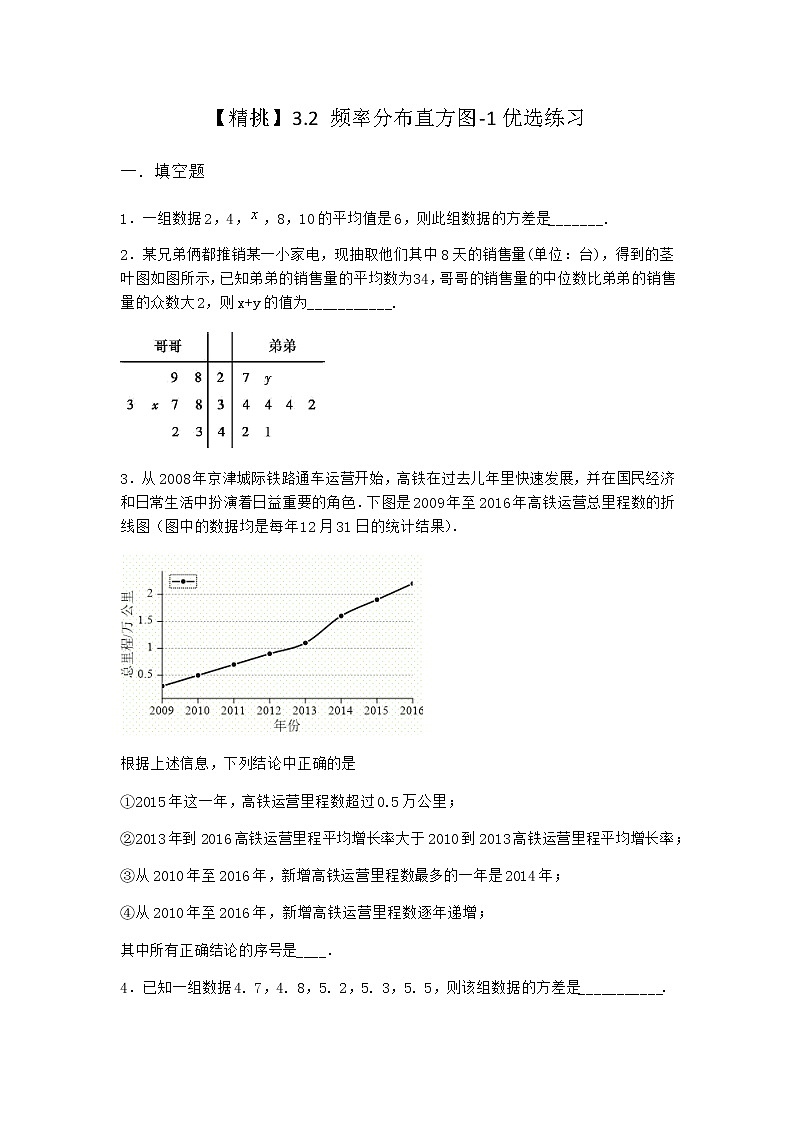
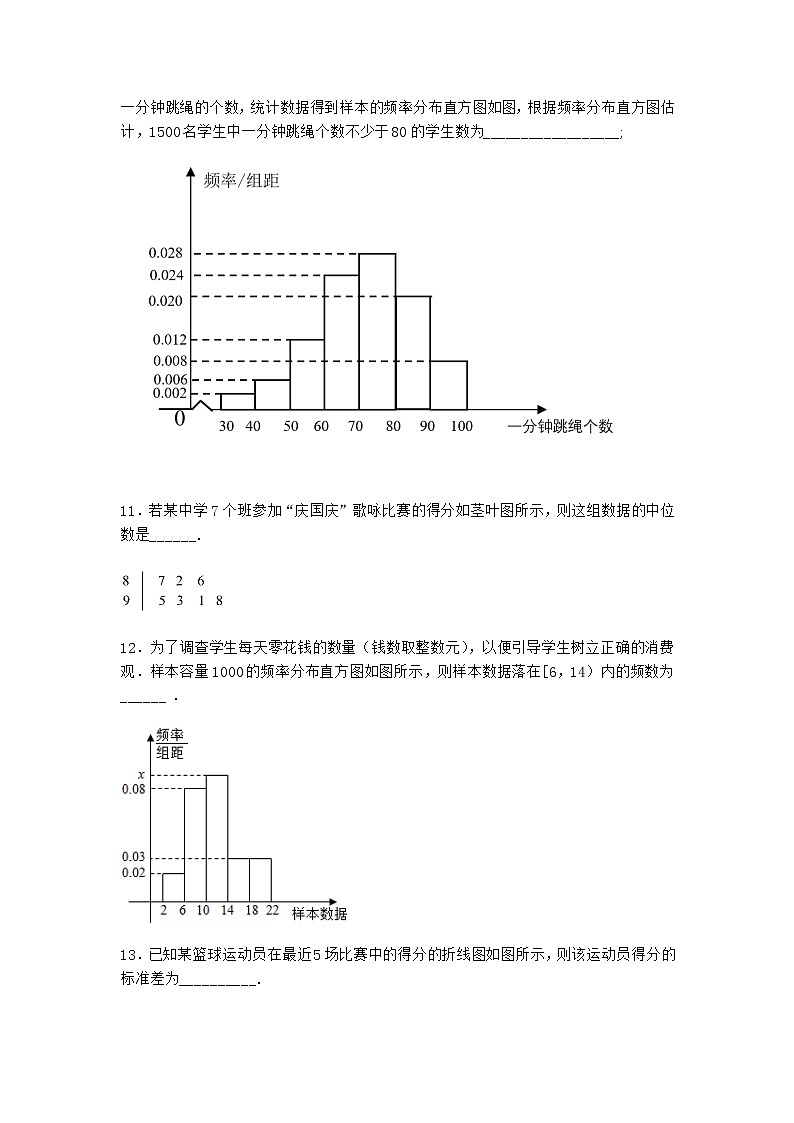
【精挑】3.2 频率分布直方图-1优选练习一．填空题1．一组数据2，4，，8，10的平均值是6，则此组数据的方差是_______.2．某兄弟俩都推销某一小家电，现抽取他们其中8天的销售量(单位：台)，得到的茎叶图如图所示，已知弟弟的销售量的平均数为34，哥哥的销售量的中位数比弟弟的销售量的众数大2，则x+y的值为___________.3．从2008年京津城际铁路通车运营开始，高铁在过去儿年里快速发展，并在国民经济和日常生活中扮演着日益重要的角色．下图是2009年至2016年高铁运营总里程数的折线图（图中的数据均是每年12月31日的统计结果）．根据上述信息，下列结论中正确的是①2015年这一年，高铁运营里程数超过0.5万公里；②2013年到2016高铁运营里程平均增长率大于2010到2013高铁运营里程平均增长率；③从2010年至2016年，新增高铁运营里程数最多的一年是2014年；④从2010年至2016年，新增高铁运营里程数逐年递增；其中所有正确结论的序号是____．4．已知一组数据4. 7，4. 8，5. 2，5. 3，5. 5，则该组数据的方差是___________．5．数组2.7？3.1？2.5？4.8？2.9？3.6的中位数为___________.6．高二足球队教练分六个项目对本队全体队员进行了测试，小华同学将自己的成绩与全体队员的平均分绘制成雷达图如图，若从中任选3个项目，则至少有两项小华的成绩高于该队平均分的选法有______种.7．在某项技能测试中，甲乙两人的成绩(单位：分)记录在如图所示的茎叶图中，其中甲的某次成绩不清晰，用字母a代替.已知甲乙成绩的平均数相等，那么甲成绩的中位数为___________.8．某班40名学生，在一次考试中统计所得平均分为80分，方差为70，后来发现有两名同学的成绩有损，甲实得80分错记为60分，乙实得70分错记为90分，则更正后的方差为______．9．若从总体中随机抽取的样本为：？？？1？1？3？2？2？4？2，则该总体标准差的点估计值是___________.(精确到0.1)10．某小学为了解学生的身体素质情况，从1500名学生中随机抽取100名，测试他们一分钟跳绳的个数，统计数据得到样本的频率分布直方图如图，根据频率分布直方图估计，1500名学生中一分钟跳绳个数不少于80的学生数为__________________;11．若某中学7个班参加“庆国庆”歌咏比赛的得分如茎叶图所示，则这组数据的中位数是______.12．为了调查学生每天零花钱的数量（钱数取整数元），以便引导学生树立正确的消费观．样本容量1000的频率分布直方图如图所示，则样本数据落在[6，14）内的频数为______ ．13．已知某篮球运动员在最近5场比赛中的得分的折线图如图所示，则该运动员得分的标准差为__________.14．某工厂对一批产品进行了抽样检测．下图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是，样本数据分组为，，，，，已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是___________．15．某中学为了解学生的数学学习情况，在3000名学生中随机抽取200名，并统计这200名学生的某次数学考试成绩，得到了样本的频率分布直方图，根据频率分布直方图，推测这3000名学生在该次数学考试中成绩不低于80分的学生人数是___________.参考答案与试题解析1．【答案】8【解析】分析：由条件求得，然后算出答案即可.详解：因为，解得所以此组数据的方差是故答案为：82．【答案】13【解析】分析：先根据弟弟的销售量的平均数为34，求得y,进而得到其众数，然后再根据哥哥的销售量的中位数比弟弟的销售量的众数大2，得到哥哥的销售量的中位数求解.详解：因为弟弟的销售量的平均数为34，所以，解得，由茎叶图知：弟弟的销售量的众数是34，因为哥哥的销售量的中位数比弟弟的销售量的众数大2，所以哥哥的销售量的中位数是36，所以，解得，所以，故答案为：133．【答案】②③【解析】分析：根据统计折线图对各选项逐一作出判断即可.详解：解析：对于①，看2014年，2015年对应的纵坐标之差，小于，①错误；对于②，连线看斜率即可，2013年到2016两点连线斜率更大，②正确；对于③，看两点纵坐标之差哪组最大，③正确；对于④，看相邻纵坐标之差是否逐年增加，显然不是，有增有减，④错误；综上，填②③．故答案为：②③4．【答案】0.092【解析】分析：先计算出均值，再由方差公式计算方差．详解：由已知均值为，所以方差为．故答案为：0.092.5．【答案】【解析】分析：根据中位数定义即可得到答案.详解：先将这组数据由小到大排列，然后可知：中位数.故答案为：6．【答案】10【解析】分析：根据雷达图，可知小华的成绩高于该队平均分的项目有3个，设为A，B，C，小华的成绩不高于该队平均分的项目有3个，设为a，b，c，然后用列举法求解即可.详解：根据雷达图，可知小华的成绩高于该队平均分的项目有3个，设为A，B，C，小华的成绩不高于该队平均分的项目有3个，设为a，b，c，从中任取3个项目，至少有两项小华的成绩高于该队平均分的选法有：(A，B，C)，(A，B，a)，(A，B，b)， (A，B，c)，(B，C，a)，(B，C，b)，(B，C，c)，(A，C，a)，(A，C，b)， (A，C，c)，共10种，故答案为：.7．【答案】21【解析】分析：由两人平均数相等求出，然后把甲成绩按从低到高排列，中间两数的均值为中位数．详解：由题意，知，解得.甲的成绩按从低到高排列：16，18，18，24，24，28，∴甲的中位数为.故答案为：21.8．【答案】60【解析】分析：先判断更正前后平均分没有变化都是分，再根据方差的概念先表示出更正前的方差和更正后的方差，比较其异同，然后整体代入即可求解.详解：因为甲实得分，记为分，少记分，乙实得分，记为分，多记分，所以总分没有变化，因此更正前后的平均分没有变化，都是分，设甲乙以外的其他同学的成绩分别为，因为更正前的方差为，所以，所以，更正后的方差为：，所以更正后的方差为，故答案为：.【点睛】关键点点睛：解答本题的关键在于分析更正前后的平均分变化情况，同时对于方差的计算公式要熟练掌握.9．【答案】【解析】分析：利用样本标准差的点估计值估计总体标准差的点估计值即可.详解：解：由已知，样本的平均值为，所以样本标准差的点估计值为，所以总体标准差的点估计值是，故答案为：.10．【答案】420【解析】分析：由频率分布直方图求得个数不少于80的学生的频率，进而求得一分钟跳绳个数不少于80的学生数，得到答案.详解：由频率分布直方图，可得个数不少于80的学生的频率为，所以1500名学生中一分钟跳绳个数不少于80的学生数为人.故答案为：.11．【答案】91【解析】分析：把7个班得分数据按从小到大的顺序排好，中间的那个就是中位数.详解：某中学7各班的得分按从小到大为：82,86,87,91,93,95,98，故中间的数据为91.故答案为：91.【点睛】本题考查了茎叶图与中位数的应用问题，解题的关键是看清所给的数据的个数，计算中位数时，看清是有偶数个数据还是奇数个数据，从而求出中位数.12．【答案】680【解析】分析：根据频率分布直方图的小矩形面积之和为1，求出x，然后再求频数.详解：根据题意得：，解得，所以样本数据落在[6，14）内的频数为：，故答案为：68013．【答案】2【解析】分析：由折线图写出每场比赛的分值并求，由求方差，进而可得标准差.详解：由图知，该运动员5场比赛的得分分别为10，13，12，14，16，则平均数为，∴方差为，所以标准差为2.故答案为：2.14．【答案】90【解析】分析：利用，中的样本个数求得样本容量，从而可求得样本中净重大于或等于98克并且小于104克的产品的个数.详解：∵样本中产品净重小于100克的频率为(0.050＋0.100)×2＝0.3，频数为36，∴样本容量为＝120.∵样本中净重大于或等于98克并且小于104克的产品的频率为(0.100＋0.150＋0.125)×2＝0.75，∴样本中净重大于或等于98克并且小于104克的产品的个数为120×0.75＝90.故答案为：9015．【答案】【解析】分析：首先计算成绩不低于80的两个小矩形的面积之和，即成绩不低于80的学生的频率，再乘以3000即可．详解：解：由频率分布直方图成绩不低于80的学生的频率为10×（0.020+0.008）＝0.28，所以成绩不低于80分的学生数是3000×＝故答案为：