数学3.2 频率分布直方图综合训练题

【特供】3.2 频率分布直方图-2作业练习

一．填空题

1．从某工厂生产线上随机抽取16件零件,测量其内径数据从小到大依次排列如:1.12,1.25,1.21,1.23,1.25,1.25,1.26,1.30,1.30,1.32,1.34,1.35,1.37,1.38,1.41,1.42.据此可估计该生产线上大约有25%的零件内径小于等于___________㎜,大约有30%的零件内径大于___________mm（单位：mm）.

2．已知五个互不相等的样本，，，，，它们的平均数为7，标准差为2，则样本数据中最大值为__________.

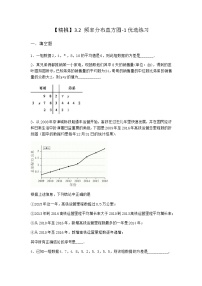
3．下图是根据某学校1000位学生的身高（单位：厘米）制成的频率分布直方图，则所调查的学生中身高在内的学生人数是______________.

4．某校从高二年级学生中随机抽取部分学生，将他们的模块测试成绩分成6组：，，，，，加以统计，得到如下图所示的频率分布直方图.已知高二年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为_________.

5．如下一组数据：10，12，25，10，30，10，13；则该组数据的中位数与众数的差为_________.

6．在样本的频率分布直方图中，某个小长方形的面积是其他小长方形面积之和的.已知样本容量是80.则该组的频数为________．

7．口罩是一种重要的医疗物资，为确保口罩供应，某工厂口罩生产线高速运转.设该工厂连续6天生产的口罩数量依次为，，，，，，（单位：万只）若，，，，，，的方差为1，且，，，，，的平均数为5，则该工厂这6天平均每天生产口罩________万只.

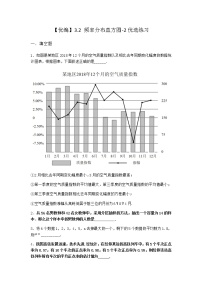
8．在某次综合素质测试中，共设有40个考场，每个考场30名考生.在考试结束后，统计了他们的成绩，得到如图所示的频率分布直方图.估计这40个考场成绩的中位数是__________.

9．若数据，，…，的方差为9，则数据，，…，的方差为__________．

10．已知样本方差，则样本的方差为_______.

11．金老师某一周五个工作日每天的工作时间(小时)是12,10,15,13,10,则这组数据的方差是________.

12．某车间将10名工人平均分成甲．乙两组加工某种零件，在单位时间内每个工人加工的合格零件数如茎叶图所示，已知两组工人在单位时间内加工的合格零件平均数都为20，则m+n=___________

13．如图是调查某学校高三年级男生，女生是否喜欢徒步运动而得到的等高条形图，阴影部分表示喜欢徒步的频率．已知该年级男生800人，女生600人（假设所有学生都参加了调查），现从所有喜欢徒步的学生中按分层抽样的方法抽取33人，则抽取的男生人数为_____．

14．某住宅小区有居民万户，从中随机抽取户，调查是否安装宽带，调查结果如下表所示：

则该小区已安装宽带的居民估计有______户．

15．已知一组数据的方差为2，则这组数据的方差为______.

参考答案与试题解析

1．【答案】     

【解析】由,所给数据是由小到大排列,从左向右查出个数据,据此可估计该生产线上大约有的零件内径小于等于.同理,,在数据中从右向左查出个数据,则大约有的零件内径大于.

【详解】

从某工厂生产线上随机抽取16件零件测量其内径数据从小到大依次排列如下:

所给数据是由小到大排列,从左向右查出个数据,第个数据为

据此可估计该生产线上大约有的零件内径小于等于.

在数据中从右向左查出5个数据,则大约有的零件内径大于.

故答案为:,

【点睛】

本题考查满足条件的内径的求法,考查数据处理能力等基础知识,考查运算求解能力.

2．【答案】10

【解析】分析：因为数据为五个互不相等的自然数，不妨设，利用已知条件可分析出，分，，三种情况讨论即可得出结果.

详解：因为数据为五个互不相等的自然数，

不妨设，

由它们的平均数为7，标准差为2，

得，方差为，

那么，

当时，

数据依次为：，

则样本的方差为，

不满足题意；

当时，

数据依次为：，

则样本的方差为，

满足题意；

当时，

，

那么，此时，

方差大于，

所以样本数据中最大值为.

故答案为：.

【点睛】

关键点睛：因为数据为五个互不相等的自然数，利用已知条件可分析出，分，，三种情况讨论是解决本题的关键.

3．【答案】650

【解析】分析：由频率分布直方图可得在内的频率，进而求解.

详解：在的学生数为.

故答案为：650

【点睛】

本题考查了频率分布直方图求频数，考查了基本运算求解能力，属于基础题.

4．【答案】480.

【解析】根据频率分布直方图计算模块测试成绩不少于60分的学生所占频率，再计算频数.

【详解】

由频率分布直方图得模块测试成绩不少于60分的学生所占频率为，

所以该模块测试成绩不少于60分的学生人数为

【点睛】

本题考查频率分布直方图以及频数，考查基本分析运算能力，属基础题.

5．【答案】2

【解析】分析：由中位数和众数的概念可得数据的中位数和众数，即可得解.

详解：由题意，该组数据的中位数为12，众数为10，

所以该组数据的中位数与众数的差为2.

故答案为：2.

【点睛】

本题考查了数据中位数及众数的求解，牢记知识点是解题关键，属于基础题.

6．【答案】16

【解析】分析：由频率分布直方图的特点可知每个小长方形的面积就是其对应的频率，从而求出该组的频率，进而可求出频数

详解：解：设该组对应的小长方形的面积为，则由题意得

，解得，

所以该组的频率为，

所以该组的频数为，

故答案为：16

【点睛】

此题考查频率分布直方图的应用，考查频数与频率的关系，属于基础题

7．【答案】2

【解析】分析：根据可求平均每天生产口罩只数.

详解：设方差为，则，其中为6天平均每天生产口罩只数，

由题设有，

故，所以，

故答案为：2.

【点睛】

本题考查样本方差和样本均值的关系，两者常见的关系为，该公式可转化为，注意公式的合理使用.

8．【答案】77.5

【解析】分析：根据中位数在左右两侧小矩形的面积相等，即可求出.

详解：中位数在左右两侧小矩形的面积相等，

从左边开始前三个小矩形的面积和为，

从左边开始前四个小矩形的面积和为，

故中位数在内，

设中位数为75+x，则，解得，

∴中位数为77.5.

故答案为：77.5.

【点睛】

本题考查由频率分布直方图估计中位数，属于基础题.

9．【答案】1

【解析】分析：利用方差公式表示已知和待求，即可得到答案.

详解：令，则.

又，

则，

∴，即数据，，…，的方差为.

故答案为：1.

【点睛】

本题考查方差的求法，可以利用方差公式推导出结果，也可以直接利用结论作答.若数据的平均数为，方差为，则数据(为常数)的平均数为，方差为.

10．【答案】8

【解析】分析：根据题意，样本的方差，根据公式，即可求解的方差

详解：由题意，样本数据的方差，

设样本的方差为，则.

点睛：本题考查了样本数据的分差的计算，熟记两组数据的方差之间的关系式是解答的关键，着重考查了推理与运算你能力.

11．【答案】

【解析】详解：【分析】直接代入方差公式。

详解：

【点睛】方差公式运算，属于简单题。

12．【答案】11

【解析】根据平均数公式分别计算得到的值，再求和.

详解：甲组的平均数，解得：

乙组的平均数，解得：，

所以.

故答案为：11

【点睛】

本题考查根据茎叶图中数据的平均数补全茎叶图，属于基础题型，本题重点考查平均数公式.

13．【答案】22

【解析】分析：先由等高条形图求出男女生喜欢徒步的学生人数，然后按比例计算所抽取的男生人数．

详解：由等高条形图知男生中喜欢徒步人数为，女生中喜欢徒步人数为，总人数为，

因此所抽取的男生数为．

故答案为：22.

【点睛】

本题考查统计图表：等高条形图，考查分层抽样．属于基础题．

14．【答案】

【解析】计算出抽样中已安装宽带的用户比例，乘以总人数，求得小区已安装宽带的居民数.

【详解】

抽样中已安装宽带的用户比例为，故小区已安装宽带的居民有户.

【点睛】

本小题主要考查用样本估计总体，考查频率的计算，属于基础题.

15．【答案】8

【解析】分析：由线性变换后新数据与原数据间方差的关系计算．

详解：的方差是．

故答案为：8.

【点睛】

本题考查方差的概念，掌握方差的性质是解题关键．数据的均值是，方差是，新数据满足（），新数据的均值是，方差是，则，．