备战2023数学新中考二轮复习重难突破（浙江专用）专题09 反比例函数及应用

这是一份备战2023数学新中考二轮复习重难突破（浙江专用）专题09 反比例函数及应用，文件包含备战2023数学新中考二轮复习重难突破浙江专用专题09反比例函数及应用解析版docx、备战2023数学新中考二轮复习重难突破浙江专用专题09反比例函数及应用原卷版docx等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。


目标点拨
1.理解反比例函数的定义，掌握反比例函数的表达式，能根据条件确定反比例函数的表达式；
2.能画出反比例函数的图象，并根据图象理解反比例函数的性质；
3.能利用反比例函数模型解决生活实际问题.
4.会解决反比例函数与一次函数的综合题
知识总结
一、反比例函数的概念
一般地，函数（k是常数，k0）叫做反比例函数。反比例函数的解析式也可以写成的形式。自变量x的取值范围是x0的一切实数，函数的取值范围也是一切非零实数。
二、反比例函数的图象
反比例函数的图象是双曲线，它有两个分支，这两个分支分别位于第一、三象限，或第二、四象限，它们关于原点对称。由于反比例函数中自变量x0，函数y0，所以，它的图象与x轴、y轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远达不到坐标轴。
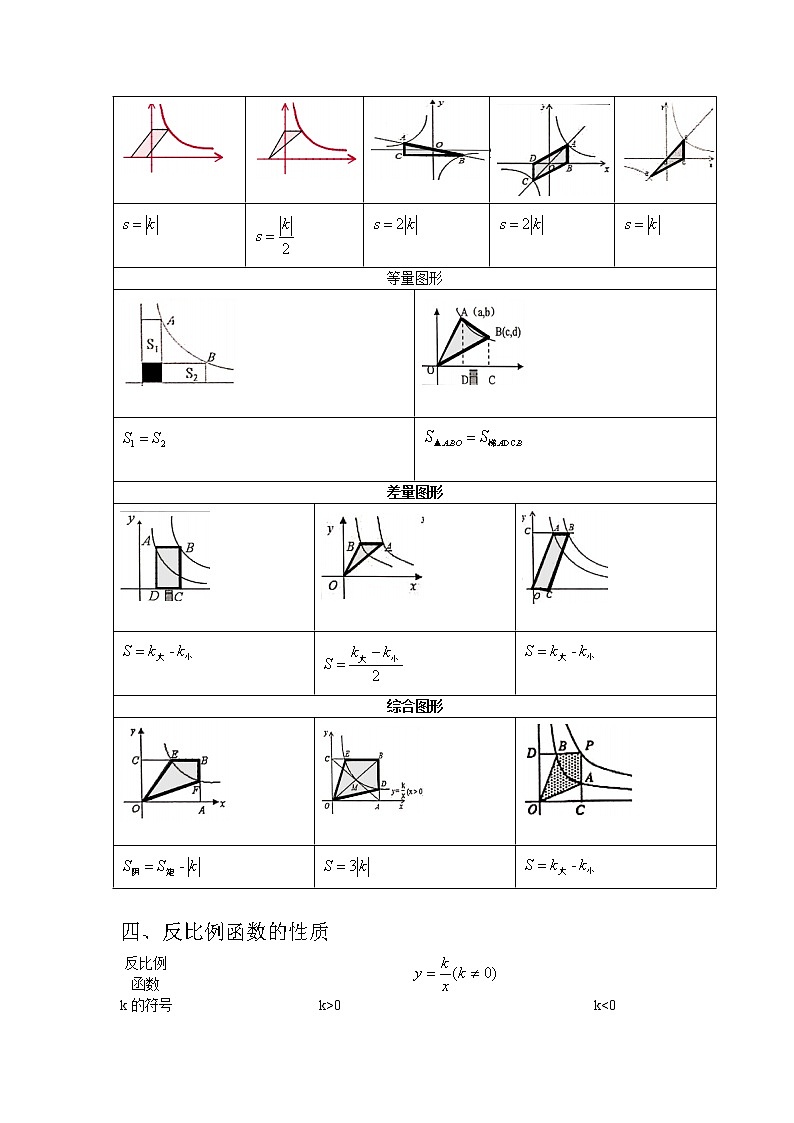
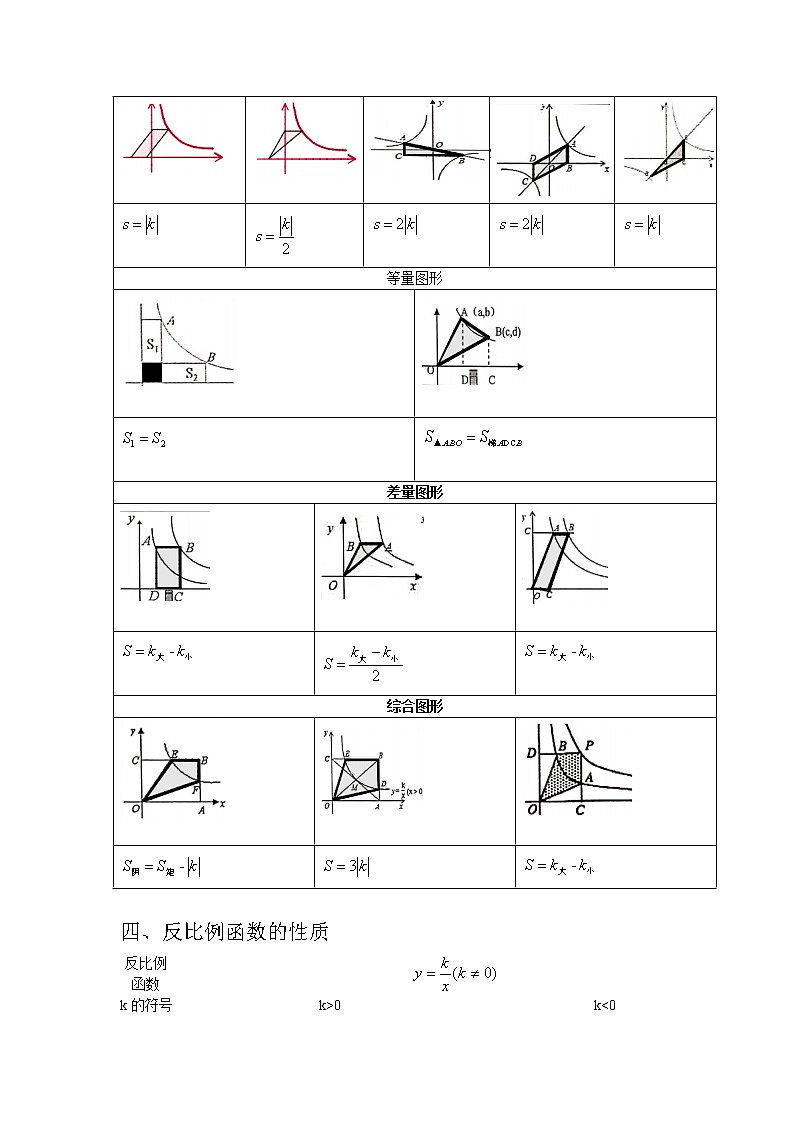
三、 反比例函数k的几何意义
下列图形中反比例函数表达式为，其中涉及两个反比例函数的，较大的k用表示，较小的k用表示，则阴影面积如下表：
基本图形




变式图形










等量图形






差量图形







综合图形








四、反比例函数的性质
反比例函数

k的符号
k>0
k<0
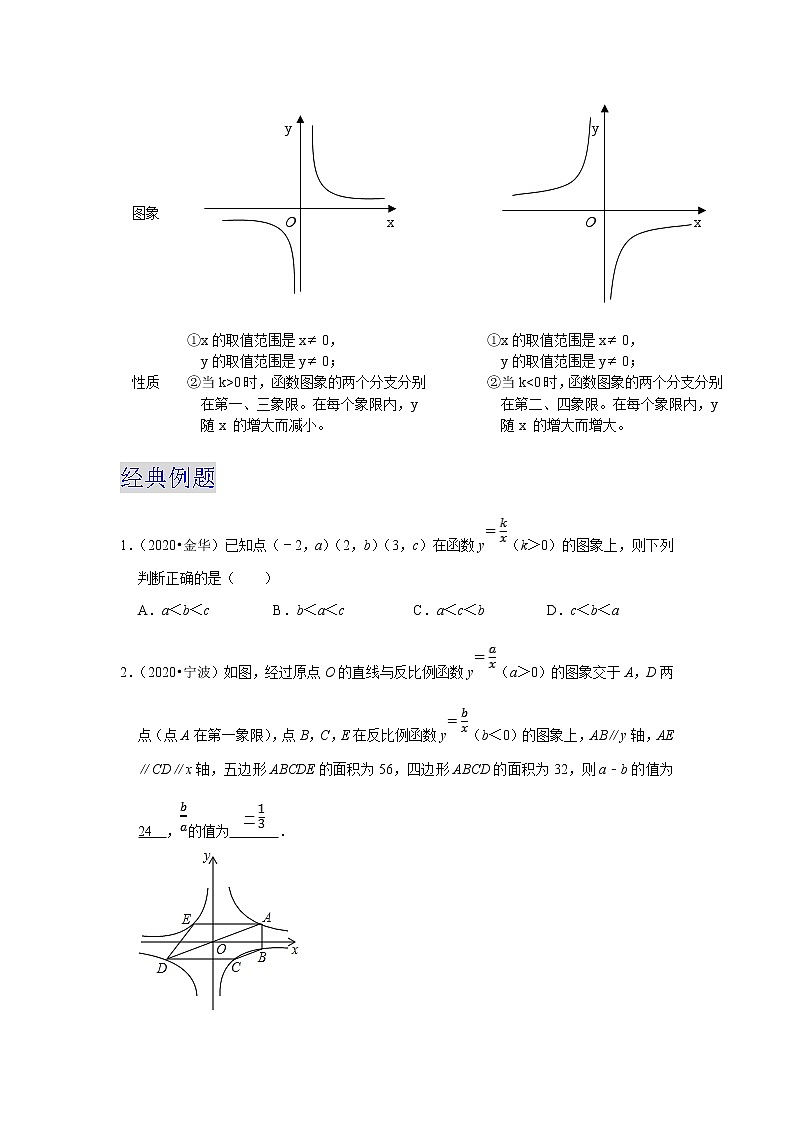
图象

y



O x





y



O x



性质
①x的取值范围是x0，
y的取值范围是y0；
②当k>0时，函数图象的两个分支分别
在第一、三象限。在每个象限内，y
随x 的增大而减小。
①x的取值范围是x0，
y的取值范围是y0；
②当k<0时，函数图象的两个分支分别
在第二、四象限。在每个象限内，y
随x 的增大而增大。

经典例题
1．（2020•金华）已知点（﹣2，a）（2，b）（3，c）在函数y（k＞0）的图象上，则下列判断正确的是（　　）
A．a＜b＜c B．b＜a＜c C．a＜c＜b D．c＜b＜a
【分析】根据反比例函数的性质得到函数y（k＞0）的图象分布在第一、三象限，在每一象限，y随x的增大而减小，则b＞c＞0，a＜0．
【解析】∵k＞0，
∴函数y（k＞0）的图象分布在第一、三象限，在每一象限，y随x的增大而减小，
∵﹣2＜0＜2＜3，
∴b＞c＞0，a＜0，
∴a＜c＜b．
故选：C．
2．（2020•宁波）如图，经过原点O的直线与反比例函数y（a＞0）的图象交于A，D两点（点A在第一象限），点B，C，E在反比例函数y（b＜0）的图象上，AB∥y轴，AE∥CD∥x轴，五边形ABCDE的面积为56，四边形ABCD的面积为32，则a﹣b的值为　24　，的值为　　．

【分析】如图，连接AC，OE，OC，OB，延长AB交DC的延长线于T，设AB交x轴于K．求出证明四边形ACDE是平行四边形，推出S△ADE＝S△ADC＝S五边形ABCDE﹣S四边形ABCD＝56﹣32＝24，推出S△AOE＝S△DEO＝12，可得ab＝12，推出a﹣b＝24．再证明BC∥AD，证明AD＝3BC，推出AT＝3BT，再证明AK＝3BK即可解决问题．
【解析】如图，连接AC，OE，OC，OB，延长AB交DC的延长线于T，设AB交x轴于K．

由题意A，D关于原点对称，
∴A，D的纵坐标的绝对值相等，
∵AE∥CD，
∴E，C的纵坐标的绝对值相等，
∵E，C在反比例函数y的图象上，
∴E，C关于原点对称，
∴E，O，C共线，
∵OE＝OC，OA＝OD，∴四边形ACDE是平行四边形，
∴S△ADE＝S△ADC＝S五边形ABCDE﹣S四边形ABCD＝56﹣32＝24，
∴S△AOE＝S△DEO＝12，
∴ab＝12，
∴a﹣b＝24，
∵S△AOC＝S△AOB＝12，
∴BC∥AD，
∴，
∵S△ACB＝32﹣24＝8，
∴S△ADC：S△ABC＝24：8＝1：3，
∴BC：AD＝1：3，
∴TB：TA＝1：3，设BT＝a，则AT＝3a，AK＝TK＝1.5k，BK＝0.5k，
∴AK：BK＝3：1，
∴，
∴．
故答案为24，．
3．（2020•衢州）如图，将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中，AB在x轴上，点G与点A重合，点F在AD上，三角板的直角边EF交BC于点M，反比例函数y（x＞0）的图象恰好经过点F，M．若直尺的宽CD＝3，三角板的斜边FG＝8，则k＝　40　．

【分析】通过作辅助线，构造直角三角形，求出MN，FN，进而求出AN、MB，表示出点F、点M的坐标，利用反比例函数k的意义，确定点F的坐标，进而确定k的值即可．
【解析】过点M作MN⊥AD，垂足为N，则MN＝CD＝3，
在Rt△FMN中，∠MFN＝30°，
∴FNMN＝3，
∴AN＝MB＝835，
设OA＝x，则OB＝x+3，
∴F（x，8），M（x+3，5），
∴8x＝（x+3）×5，
解得，x＝5，
∴F（5，8），
∴k＝5×840．
故答案为：40．

4．（2020•温州）点P，Q，R在反比例函数y（常数k＞0，x＞0）图象上的位置如图所示，分别过这三个点作x轴、y轴的平行线．图中所构成的阴影部分面积从左到右依次为S1，S2，S3．若OE＝ED＝DC，S1+S3＝27，则S2的值为　　．

【分析】设CD＝DE＝OE＝a，则P（，3a），Q（，2a），R（，a），推出CP，DQ，ER，推出OG＝AG，OF＝2FG，OFGA，推出S1S3＝2S2，根据S1+S3＝27，求出S1，S3，S2即可．
【解析】∵CD＝DE＝OE，
∴可以假设CD＝DE＝OE＝a，
则P（，3a），Q（，2a），R（，a），
∴CP，DQ，ER，
∴OG＝AG，OF＝2FG，OFGA，
∴S1S3＝2S2，
∵S1+S3＝27，
∴S3，S1，S2，
故答案为．
5．（2020•湖州）如图，已知在平面直角坐标系xOy中，Rt△OAB的直角顶点B在x轴的正半轴上，点A在第一象限，反比例函数y（x＞0）的图象经过OA的中点C．交AB于点D，连结CD．若△ACD的面积是2，则k的值是　　．

【分析】作辅助线，构建直角三角形，利用反比例函数k的几何意义得到S△OCE＝S△OBDk，根据OA的中点C，利用△OCE∽△OAB得到面积比为1：4，代入可得结论．
【解析】连接OD，过C作CE∥AB，交x轴于E，

∵∠ABO＝90°，反比例函数y（x＞0）的图象经过OA的中点C，
∴S△COE＝S△BOD，S△ACD＝S△OCD＝2，
∵CE∥AB，
∴△OCE∽△OAB，
∴，
∴4S△OCE＝S△OAB，
∴4k＝2+2k，
∴k，
故答案为：．
6．（2020•宁波）如图，过原点的直线与反比例函数y（k＞0）的图象交于A，B两点，点A在第一象限．点C在x轴正半轴上，连结AC交反比例函数图象于点D．AE为∠BAC的平分线，过点B作AE的垂线，垂足为E，连结DE．若AC＝3DC，△ADE的面积为8，则k的值为　6　．

【分析】连接OE，CE，过点A作AF⊥x轴，过点D作DH⊥x轴，过点D作DG⊥AF；由AB经过原点，则A与B关于原点对称，再由BE⊥AE，AE为∠BAC的平分线，
可得AD∥OE，进而可得S△ACE＝S△AOC；设点A（m，），由已知条件AC＝3DC，DH∥AF，可得3DH＝AF，则点D（3m，），证明△DHC∽△AGD，得到S△HDCS△ADG，所以S△AOC＝S△AOF+S梯形AFHD+S△HDCk12；即可求解；
【解析】连接OE，CE，过点A作AF⊥x轴，过点D作DH⊥x轴，过点D作DG⊥AF，

∵过原点的直线与反比例函数y（k＞0）的图象交于A，B两点，
∴A与B关于原点对称，
∴O是AB的中点，
∵BE⊥AE，
∴OE＝OA，
∴∠OAE＝∠AEO，
∵AE为∠BAC的平分线，
∴∠DAE＝∠AEO，
∴AD∥OE，
∴S△ACE＝S△AOC，
∵AC＝3DC，△ADE的面积为8，
∴S△ACE＝S△AOC＝12，
设点A（m，），
∵AC＝3DC，DH∥AF，
∴3DH＝AF，
∴D（3m，），
∵CH∥GD，AG∥DH，
∴△DHC∽△AGD，
∴S△HDCS△ADG，
∵S△AOC＝S△AOF+S梯形AFHD+S△HDCk（DH+AF）×FH+S△HDCk2mk12，
∴2k＝12，
∴k＝6；
故答案为6；
（另解）连结OE，由题意可知OE∥AC，
∴S△OAD＝S△EAD＝8，
易知△OAD的面积＝梯形AFHD的面积，
设A的纵坐标为3a，则D的纵坐标为a，
∴（3a+a）（）＝16，
解得k＝6．

7．（2020•绍兴）如图，矩形ABCD的两边分别与坐标轴平行，顶点A，C都在双曲线y（常数k＞0，x＞0）上，若顶点D的坐标为（5，3），则直线BD的函数表达式是　yx　．

【分析】利用矩形的性质和反比例函数图象上点的坐标特征得到A（，3），C（5，），所以B（，），然后利用待定系数法求直线BD的解析式．
【解析】∵D（5，3），
∴A（，3），C（5，），
∴B（，），
设直线BD的解析式为y＝mx+n，
把D（5，3），B（，）代入得，解得，
∴直线BD的解析式为yx．
故答案为yx．
8．（2019•湖州）如图，已知在平面直角坐标系xOy中，直线yx﹣1分别交x轴，y轴于点A和点B，分别交反比例函数y1（k＞0，x＞0），y2（x＜0）的图象于点C和点D，过点C作CE⊥x轴于点E，连结OC，OD．若△COE的面积与△DOB的面积相等，则k的值是　2　．

【分析】求出直线yx﹣1与y轴的交点B的坐标和直线yx﹣1与y2（x＜0）的交点D的坐标，再由△COE的面积与△DOB的面积相等，列出k的方程，便可求得k的值．
【解析】令x＝0，得yx﹣1＝﹣1，
∴B（0，﹣1），
∴OB＝1，
把yx﹣1代入y2（x＜0）中得，x﹣1（x＜0），
解得，x＝1，
∴，
∴，
∵CE⊥x轴，
∴，
∵△COE的面积与△DOB的面积相等，
∴，
∴k＝2，或k＝0（舍去）．
经检验，k＝2是原方程的解．
故答案为：2．
9．（2020•衢州）如图，在平面直角坐标系中，O为坐标原点，▱ABCD的边AB在x轴上，顶点D在y轴的正半轴上，点C在第一象限，将△AOD沿y轴翻折，使点A落在x轴上的点E处，点B恰好为OE的中点，DE与BC交于点F．若y（k≠0）图象经过点C，且S△BEF＝1，则k的值为　24　．

【分析】连接OC，BD，根据折叠的性质得到OA＝OE，得到OE＝2OB，求得OA＝2OB，设OB＝BE＝x，则OA＝2x，根据平行四边形的性质得到CD＝AB＝3x，根据相似三角形的性质得到，求得S△BDF＝3，S△CDF＝9，于是得到结论．
【解析】连接OC，BD，

∵将△AOD沿y轴翻折，使点A落在x轴上的点E处，
∴OA＝OE，
∵点B恰好为OE的中点，
∴OE＝2OB，
∴OA＝2OB，
设OB＝BE＝x，则OA＝2x，
∴AB＝3x，
∵四边形ABCD是平行四边形，
∴CD＝AB＝3x，
∵CD∥AB，
∴△CDF∽△BEF，
∴，
∵S△BEF＝1，
∴S△BDF＝3，S△CDF＝9，
∴S△BCD＝12，
∴S△CDO＝S△BDC＝12，
∴k的值＝2S△CDO＝24．

10．（2020•台州）小明同学训练某种运算技能，每次训练完成相同数量的题目，各次训练题目难度相当．当训练次数不超过15次时，完成一次训练所需要的时间y（单位：秒）与训练次数x（单位：次）之间满足如图所示的反比例函数关系．完成第3次训练所需时间为400秒．
（1）求y与x之间的函数关系式；
（2）当x的值为6，8，10时，对应的函数值分别为y1，y2，y3，比较（y1﹣y2）与（y2﹣y3）的大小：y1﹣y2　＞　y2﹣y3．

【分析】（1）设y与x之间的函数关系式为：y，把（3，400）代入y即可得到结论，
（2）把x＝6，8，10分别代入y得到求得y1，y2，y3值，即可得到结论．
【解析】（1）设y与x之间的函数关系式为：y，
把（3，400）代入y得，400，
解得：k＝1200，
∴y与x之间的函数关系式为y；
（2）把x＝6，8，10分别代入y得，y1200，y2150，y3120，
∵y1﹣y2＝200﹣150＝50，y2﹣y3＝150﹣120＝30，
∵50＞30，
∴y1﹣y2＞y2﹣y3，
故答案为：＞．
11．（2020•杭州）设函数y1，y2（k＞0）．
（1）当2≤x≤3时，函数y1的最大值是a，函数y2的最小值是a﹣4，求a和k的值．
（2）设m≠0，且m≠﹣1，当x＝m时，y1＝p；当x＝m+1时，y1＝q．圆圆说：“p一定大于q”．你认为圆圆的说法正确吗？为什么？
【分析】（1）由反比例函数的性质可得，①；a﹣4，②；可求a的值和k的值；
（2）设m＝m0，且﹣1＜m0＜0，将x＝m0，x＝m0+1，代入解析式，可求p和q，即可判断．
【解析】（1）∵k＞0，2≤x≤3，
∴y1随x的增大而减小，y2随x的增大而增大，
∴当x＝2时，y1最大值为，①；
当x＝2时，y2最小值为a﹣4，②；
由①，②得：a＝2，k＝4；
（2）圆圆的说法不正确，
理由如下：设m＝m0，且﹣1＜m0＜0，
则m0＜0，m0+1＞0，
∴当x＝m0时，p＝y1，
当x＝m0+1时，q＝y10，
∴p＜0＜q，
∴圆圆的说法不正确．
12．（2020•金华）如图，在平面直角坐标系中，正六边形ABCDEF的对称中心P在反比例函数y（k＞0，x＞0）的图象上，边CD在x轴上，点B在y轴上，已知CD＝2．
（1）点A是否在该反比例函数的图象上？请说明理由；
（2）若该反比例函数图象与DE交于点Q，求点Q的横坐标；
（3）平移正六边形ABCDEF，使其一边的两个端点恰好都落在该反比例函数的图象上，试描述平移过程．

【分析】（1）过点P作x轴垂线PG，连接BP，可得BP＝2，G是CD的中点，所以P（2，）；
（2）易求D（3，0），E（4，），待定系数法求出DE的解析式为x﹣3，联立反比例函数与一次函数即可求点Q；
（3）E（4，），F（3，2），将正六边形向左平移两个单位后，E（2，），F（1，2），则点E与F都在反比例函数图象上；
【解析】（1）过点P作x轴垂线PG，连接BP，

∵P是正六边形ABCDEF的对称中心，CD＝2，
∴BP＝2，G是CD的中点，
∴PG，
∴P（2，），
∵P在反比例函数y上，
∴k＝2，
∴y，
由正六边形的性质，A（1，2），
∴点A在反比例函数图象上；
（2）D（3，0），E（4，），
设DE的解析式为y＝mx+b，
∴，
∴，
∴yx﹣3，
联立方程解得x，
∴Q点横坐标为；
（3）A（1，2），B（0，），C（1，0），D（3，0），E（4，），F（3，2），
设正六边形向左平移m个单位，向上平移n个单位，则平移后点的坐标分别为
∴A（1﹣m，2n），B（﹣m，n），C（1﹣m，n），D（3﹣m，n），E（4﹣m，n），F（3﹣m，2n），
①将正六边形向左平移两个单位后，E（2，），F（1，2）；
则点E与F都在反比例函数图象上；
②将正六边形向右平移一个单位，再向上平移个单位后，C（2，），B（1，2）
则点B与C都在反比例函数图象上；

13．（2020•舟山）如图，在直角坐标系中，已知点B（4，0），等边三角形OAB的顶点A在反比例函数y的图象上．
（1）求反比例函数的表达式．
（2）把△OAB向右平移a个单位长度，对应得到△O'A'B'当这个函数图象经过△O'A'B'一边的中点时，求a的值．

【分析】（1）过点A作AC⊥OB于点C，根据等边三角形的性质得出点A坐标，用待定系数法求得反比例函数的解析式即可；
（2）分两种情况讨论：①反比例函数图象过AB的中点；②反比例函数图象过AO的中点．分别过中点作x轴的垂线，再根据30°角所对的直角边是斜边的一半得出中点的纵坐标，代入反比例函数的解析式得出中点坐标，再根据平移的法则得出a的值即可．
【解析】（1）过点A作AC⊥OB于点C，

∵△OAB是等边三角形，
∴∠AOB＝60°，OCOB，
∵B（4，0），
∴OB＝OA＝4，
∴OC＝2，AC＝2．
把点A（2，2）代入y，得k＝4．
∴反比例函数的解析式为y；
（2）分两种情况讨论：
①点D是A′B′的中点，过点D作DE⊥x轴于点E．

由题意得A′B′＝4，∠A′B′E＝60°，
在Rt△DEB′中，B′D＝2，DE，B′E＝1．
∴O′E＝3，
把y代入y，得x＝4，
∴OE＝4，
∴a＝OO′＝1；
②如图3，点F是A′O′的中点，过点F作FH⊥x轴于点H．

由题意得A′O′＝4，∠A′O′B′＝60°，
在Rt△FO′H中，FH，O′H＝1．
把y代入y，得x＝4，
∴OH＝4，
∴a＝OO′＝3，
综上所述，a的值为1或3．