冀教版九年级下册30.2 二次函数的图像和性质获奖ppt课件

这是一份冀教版九年级下册30.2 二次函数的图像和性质获奖ppt课件，共42页。PPT课件主要包含了课前导入，新课精讲，学以致用，课堂小结，情景导入，探索新知，典题精讲，函数的上下移动，易错提醒，小试牛刀等内容，欢迎下载使用。

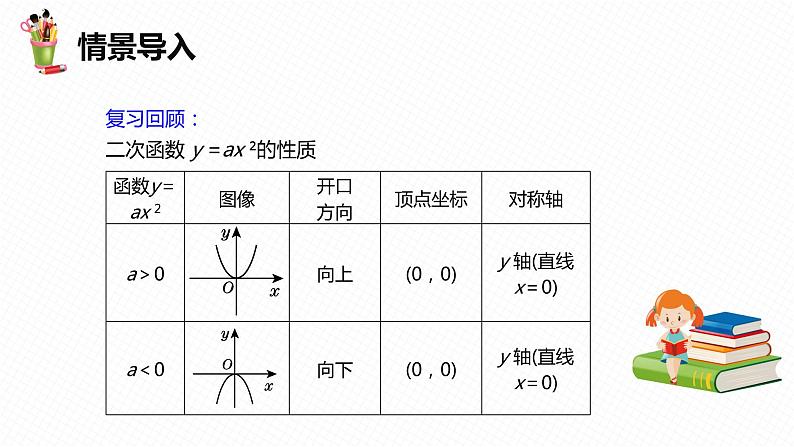
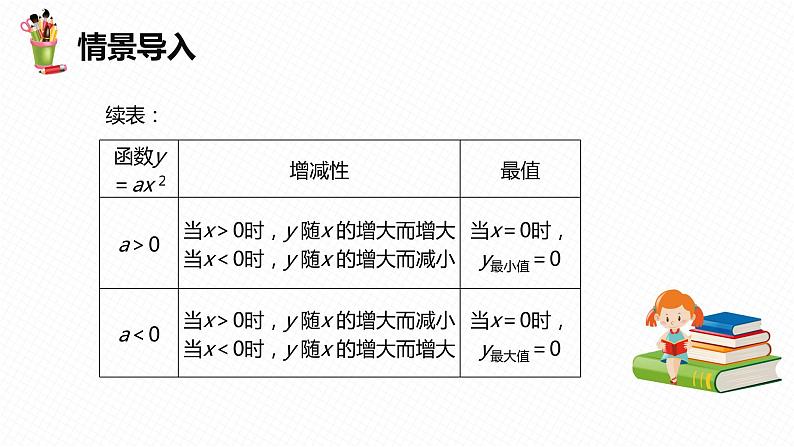
复习回顾：二次函数 y =ax ²的性质
二次函数 y =ax 2+c 的图像
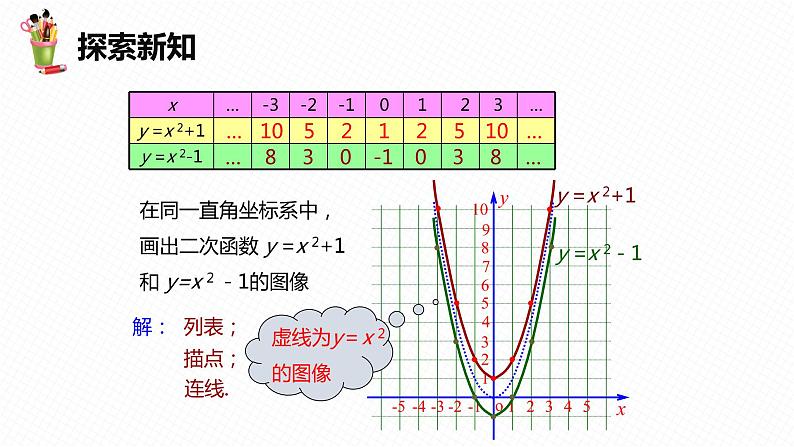
1.画二次函数 y = x 2+1的图像，你是怎样画的？与同伴进行 交流.2.二次函数 y =x 2+1的图像与二次函数 y =x 2 的图像有什么关 系？它是轴对称图形吗？它的开口方向、对称轴和顶点坐 标分别是什么？ 二次函数 y = x 2-1的图像呢？
在同一直角坐标系中，画出二次函数 y =x 2+1和 y=x 2 －1的图像
虚线为y＝x 2的图像
导引：根据二次函数 y＝ax 2＋c (a≠0)的图像的对称轴是 y 轴直接选择．
函数 y＝ax 2＋c (a≠0)与函数 y＝ax 2(a≠0)图像特征：只有顶点坐标不同，其他都相同．
1 抛物线 y＝ax 2＋(a－2)的顶点在x 轴的下方，则a 的取 值范围是____________．2 在平面直角坐标系中，下列函数的图像经过原点的是(　　) A．y＝ B．y＝－2x－3 C．y＝2x 2＋1 D．y＝5x
3 在平面直角坐标系中，抛物线 y＝x 2－1与x 轴的交 点的个数是(　　) A．3 B．2 C．1 D．0
二次函数 y＝2x 2－3的图像是一条抛物线，下列关于该抛物线的说法，正确的是(　　)A．抛物线开口向下B．抛物线经过点(2，3)C．抛物线的对称轴是直线x＝1D．抛物线与x 轴有两个交点
在二次函数：①y＝3x 2 ； ② y＝ x 2＋1；③ y＝－ x 2－3中，图像开口大小顺序用序号表示为(　　 )A．①>②>③ B．①>③>②C．②>③>① D．②>①>③
二次函数 y＝ax 2+c 的性质
思考：(1)抛物线 y=x 2+1，y =x 2－1的开口方向、对称轴、 顶点各是什么?(2)抛物线 y =x 2+1，y =x 2－1与抛物线 y =x 2有什么关系？
抛物线 y =x 2+1：开口向上，对称轴是y 轴，顶点为(0，1).抛物线 y =x 2－1：开口向上，对称轴是y轴，顶点为(0，－1).
二次函数 y＝ax 2＋c (a≠0)的图像和性质
例2 已知点(－7，y1)，(3，y2)，(－1，y3)都在抛物线 y＝ ax 2＋k (a＞0)上，则(　　) A．y1＜y2＜y3　 B．y1＜y3＜y2 　 C．y3＜y2＜y1　 D．y2＜y1＜y3 ∵抛物线 y＝ax 2＋k (a＞0)关于y 轴对称，且点(3，y2) 在抛物线上，∴点(－3，y2)也在抛物线上． ∵(－7，y1)，(－3，y2)，(－1，y3)三点都在对称轴左 侧，在y 轴左侧时，y 随x 的增大而减小，且－7＜－3 ＜－1，∴y3＜y2＜y1.
对于在抛物线的对称轴两侧的函数值的大小比较，运用转化思想．先根据对称性将不在对称轴同侧的点转化为在对称轴同侧的点，再运用二次函数的增减性比较大小．
1 对于二次函数 y＝3x 2＋2，下列说法错误的是(　　) A．最小值为2 B．图像与x 轴没有公共点 C．当x<0时，y 随x 的增大而增大 D．图像的对称轴是y 轴2 已知点(x1，y1)，(x2，y2)均在抛物线 y＝x 2－1上，下列说法正确的是(　　) A．若y1＝y2，则x1＝x2 B．若x1＝－x2，则y1＝－y2 C．若0y2 D．若x1y2
二次函数 y＝ax 2+c 与y＝ax 2之间的关系
观察知1中抛物线y =x 2+1，抛物线y =x 2－1与抛物线y =x 2，它们之间有什么关系？
抛物线y =x 2+1，y =x 2－1与抛物线y =x 2的关系：
抛物线 y =x 2－1
抛物线 y =x 2+1
例3 将二次函数 y＝x 2的图像向下平移1个单位， 则平移后的图像对应的二次函数的表达式为(　　) A．y＝x 2－1 　B．y＝x 2＋1　 C．y＝(x－1)2　 D．y＝(x＋1)2导引：由“上加下减”的原则可知，将二次函数 y＝x 2的图 象向下平移1个单位，则平移后的图像对应的二 次函数的表达式为 y＝x 2－1.
平移的方向决定是加还是减，平移的距离决定加或减的数值．
例4 抛物线y＝ax 2＋c 与抛物线 y＝－5x 2的形状相同，开口方 向一样，且顶点坐标为(0，3)，则其所对应的函数表达式是 什么？它是由抛物线 y＝－5x 2怎样平移得到的？导引：由两抛物线的形状、开口方向相同，可确定a 的值；再由顶 点坐标为(0，3)可确定c 的值，从而可确定平移的方向和距离．
解：因为抛物线 y＝－5x 2与抛物线 y＝ax 2＋c 的形状相同， 开口方向一样，所以a＝－5.又因为抛物线y＝ax 2＋c 的顶点坐标为(0，3)，所以c＝3，其所对应的函数表 达式为 y＝－5x 2＋3，它是由抛物线 y＝－5x 2向上平移 3个单位得到的．
根据二次函数y＝ax 2＋c 的图像和性质来解此类问题．a 确定抛物线的形状及开口方向，c 的正负和绝对值大小确定上下平移的方向和距离．
1 抛物线 y＝2x 2＋1是由抛物线 y＝2x 2 (　　)得到的． A．向上平移2个单位长度 B．向下平移2个单位长度 C．向上平移1个单位长度 D．向下平移1个单位长度2 如果将抛物线 y＝x 2＋2向下平移1个单位长度，那么所得新抛物线的表达式是(　　) A．y＝(x－1)2＋2 B．y＝(x＋1)2＋2 C．y＝x 2＋1 D．y＝x 2＋3
能否通过上下平移二次函数y＝ x 2的图像，使得到的新的函数图像过点(3，－3)？若能，说出平移的方向和距离；若不能，说明理由．
易错点：对平移的规律理解不透彻
能．设平移后的图像对应的二次函数表达式为y＝ x 2＋b，将点(3，－3)的坐标代入表达式，得b＝－6.所以平移的方向是向下，平移的距离是6个单位长度．
已知抛物线y＝ x 2＋1具有如下性质：该抛物线上任意一点到定点F (0，2)的距离与到x 轴的距离始终相等，如图，点M 的坐标为( ，3)，P 是抛物线y＝ x 2＋1上一个动点，则△PMF 周长的最小值是(　　)A．3 B．4 C．5 D．6
在同一坐标系中，一次函数y＝－mx＋n 2与二次函数 y＝x 2＋m 的图像可能是(　　)
3 抛物线 y＝ax 2＋k 的顶点坐标是(0，2)，且形状及开 口方向与抛物线y＝－ x 2相同． (1)确定a，k 的值； (2)画出抛物线y＝ax 2＋k.
如图，顶点M 在y 轴上的抛物线与直线 y＝x＋1相交于A，B 两点，且点A 在x 轴上，点B 的横坐标为2，连接AM，BM. (1)求抛物线的函数表达式； (2)判断△ABM 的形状，并说明理由．
(1)∵A点为直线 y＝x＋1与x 轴的交点，∴A(－1，0)．又B 点的横坐标为2，代入 y＝x＋1可求得y＝3，∴B (2，3)． ∵抛物线顶点在y 轴上，∴可设抛物线的表达式为y＝ax 2＋c， 把A，B 两点坐标代入可得 解得 ∴抛物线的表达式为y＝x 2－1.(2)△ABM 为直角三角形，理由如下：由(1)中求得的抛物线 表达式为y＝x 2－1可知M 点的坐标为(0，－1)， ∴AM＝ ，AB＝ BM＝ ∴AM 2＋AB 2＝2＋18＝20＝BM 2. ∴△ABM 为直角三角形．
5 如图，抛物线 y＝－ x 2＋2与x 轴交于A，B 两点，其 中点A 在x 轴的正半轴上，点B 在x 轴的负半轴上． (1)试写出该抛物线的对称轴和顶点C 的坐标． (2)在抛物线上是否存在一点M，使△MAC ≌ △OAC？ 若存在，求出点M 的坐标；若不存在，请说明理由．
(1)抛物线的对称轴是y 轴，顶点C 的 坐标为(0，2)．
廊桥是我国古老的文化遗产，如图是一座抛物线形廊桥的示意 图．已知抛物线对应的函数关系式为y＝－ x 2＋10，为保护 廊桥的安全，在该抛物线上距水面AB 高为8 m的点E，F 处要 安装两盏警示灯，求这两盏灯的水平距离．( ≈2.24，结果 精确到1 m)
当x <0时，y 随着x 的增大而减小.当x >0时，y 随着x 的增大而增大.
当x <0时，y 随着x 的增大而增大.当x >0时，y 随着x 的增大而减小.
二次函数y =ax 2+c 的图像与性质
x =0时，y最小= c
x =0时，y最大=c
抛物线y =ax 2 +c (a≠0)的图像可由y =ax 2的图像通过上下平移|c |个单位得到.