初中数学冀教版九年级下册30.4 二次函数的应用完整版课件ppt

这是一份初中数学冀教版九年级下册30.4 二次函数的应用完整版课件ppt，共42页。PPT课件主要包含了课前导入，新课精讲，学以致用，课堂小结，情景导入，探索新知，二次函数的最值，典题精讲，小试牛刀等内容，欢迎下载使用。

对于某些实际问题，如果其中变量之间的关系可以用二次函数模型来刻画，那么我们就可以利用二次函数的图象和性质来研究．
1．当自变量的取值范围是全体实数时，函数在顶点处取得最值． 即当x＝－ 时，y最值＝ .当a＞0时，在顶点处取得 最小值，此时不存在最大值；当a＜0时，在顶点处取得最大值， 此时不存在最小值．
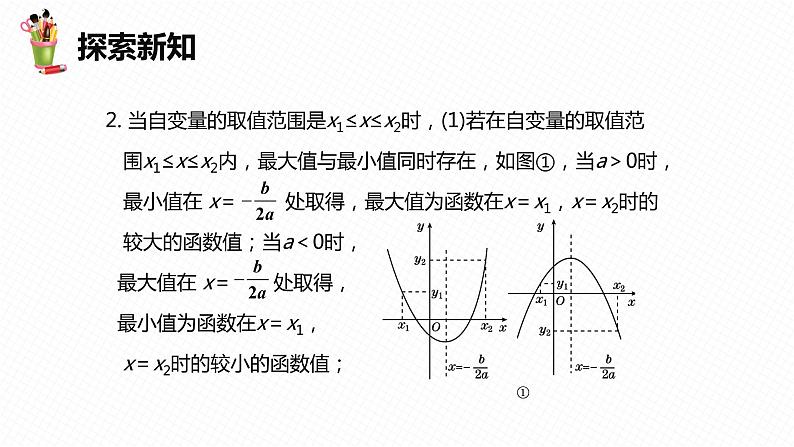
2. 当自变量的取值范围是x1≤x≤x2时，(1)若在自变量的取值范 围x1≤x≤x2内，最大值与最小值同时存在，如图①，当a＞0时， 最小值在 x＝ 处取得，最大值为函数在x＝x1，x＝x2时的 较大的函数值；当a＜0时， 最大值在 x＝ 处取得， 最小值为函数在x＝x1， x＝x2时的较小的函数值；
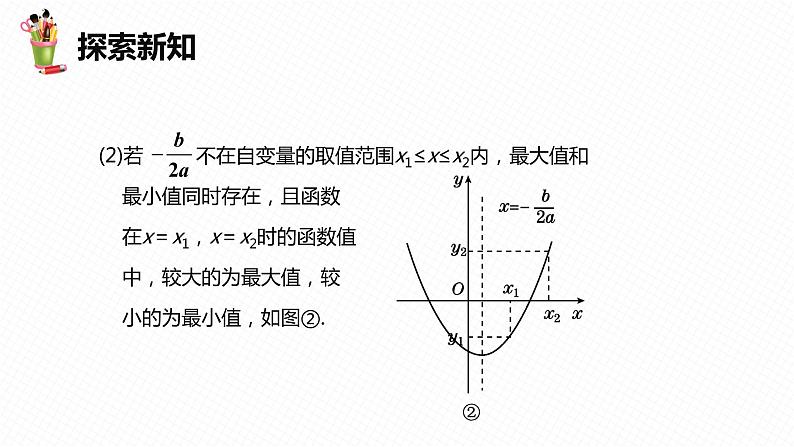
(2)若 不在自变量的取值范围x1≤x≤x2内，最大值和 最小值同时存在，且函数 在x＝x1，x＝x2时的函数值 中，较大的为最大值，较 小的为最小值，如图②.
导引：先求出抛物线 y＝x 2－2x－3的顶点坐标，然后 看顶点的横坐标是否在所规定的自变量的取值 范围内，根据不同情况求解，也可画出图象， 利用图象求解．
例1 分别在下列范围内求函数 y＝x 2－2x－3的最值： (1)0＜x＜2；(2)2≤x≤3.
解：∵y＝x 2－2x－3＝(x－1)2－4， ∴图象的顶点坐标为(1，－4)． (1)∵x＝1在0＜x＜2范围内，且a＝1＞0， ∴当x＝1时，y 有最小值，y最小值＝－4. ∵x＝1是0＜x＜2范围的中点，在直线x＝1两侧的 图象左右对称，端点处取不到， ∴不存在最大值．
(2)∵x＝1不在2≤x≤3范围内(如图)， 而函数 y＝x 2－2x－3(2≤x≤3)的图象是抛物线 y＝x 2－2x－3的一部分，且当2≤x≤3时， y 随x 的增大而增大， ∴当x＝3时， y最大值＝32－2×3－3＝0； 当x＝2时， y最小值＝22－2×2－3＝－3.
求函数在自变量某一取值范围内的最值，可根据函数增减性进行讨论，或画出函数的图象，借助于图象的直观性求解．
1 二次函数 y＝x 2－4x＋c 的最小值为0，则c 的值为(　　) A．2 B．4 C．－4 D．16已知0≤x≤ ，那么函数 y＝－2x 2＋8x－6的最大值是(　　) A．－6　　　 B．－2.5　　　 C．2　　 　 D．不能确定
已知y＝－x (x＋3－a)＋1是关于x 的二次函数，当x 的取值范围在 1≤x≤5时，若y 在x＝1时取得最大值，则实数a 的取值情况是(　　) A．a＝9 B．a＝5 C．a≤9 D．a≤54 二次函数 y＝2x 2－6x＋1，当0≤x≤5时，y 的取值范围__________．
若二次函数 y＝x 2＋ax＋5的图象关于直线 x＝－2对称， 且当m≤x≤0时，y 有最大值5，最小值1，则m 的取值范 围是______________．
利用二次函数求几何图形的面积的最值的一般步骤：(1)引入自变量；(2)用含有自变量的代数式分别表示与所求几何图形相 关的量；(3)由几何图形的特征，列出其面积的计算公式，并且 用函数表示这个面积；(4)根据函数的关系式及自变量的取值范围求出其最值．
用总长度为24 m的不锈钢材料制成如图所示的外观为矩形的框架，其横档和竖档分别与AD，AB平行. 设AB=x m，当x为多少时，矩形框架ABCD的面积S最大?最大面积是多少平方米？
1.当矩形的宽AB=x m时，如何用包含x 的代数式表示矩形的长BC ? 2.矩形的面积S 与矩形的宽x 之间的等量关系是什么? 3.你能写出矩形的面积S 与矩形的宽x 之间的函数表达式吗? 4.请用配方法将所得到的二次函数一般式转化成顶点式. 5.该二次函数有没有最大值?最大值是多少?此时x 的值是多少?
∵∴ 当x =3时，S 有最大值，且S最大＝12m2 答：当x=3时，矩形框架ABCD 的面积S 最大， 最大面积为12 m2.
例3 如图，已知△ABC 的面积为2 400 cm2，底边BC 长为80cm. 若点D 在BC 边上，E 在AC 边上，F 在AB 边上，且四 边形BDEF 为平行四边形，设BD＝x (cm)， S▱BDEF＝y (cm2)，求： (1)y 与x 之间的函数关系式． (2)自变量x 的取值范围． (3)当x 为何值时，y 取得最大值？最大值是多少？
导引：(1)可分别设出△DCE 的边CD上的高和△ABC 的边BC 上的高，根据条件求出△ABC 的边BC 上的高，再利用 相似找出其他等量关系，然后设法用x 表示▱BDEF 的边 BD上的高；(2)BD 在BC 边上，最长不超过BC；(3)根据 x 的取值范围及求最值的方法解题．
解：(1)设△DCE 的边CD上的高为h cm，△ABC 的边BC上的 高为b cm，则有S▱BDEF＝xh (cm2)． ∵S△ABC＝ BC·b， ∴2 400＝ ×80b.∴b＝60. ∵四边形BDEF 为平行四边形， ∴DE∥AB.∴△EDC∽△ABC. ∴ ∴y＝x· ＝－ x 2＋60x，即y＝－ x 2＋60x.
(2)自变量x 的取值范围是0＜x＜80. (3)由(1)可得 y ＝－ (x－40)2＋1 200. ∵a＝－ ＜0，0＜x＜80， ∴当x＝40时，y 取得最大值，最大值是1 200.
本题利用数形结合思想，先利用相似三角形找出各边的关系，再代入数值，用x 表示出h，进而得到 y 与x 之间的函数关系式，利用建模思想，建立用二次函数求几何图形的最大面积的模型，再利用配方法求出最大面积．
如图，已知AB＝2，点C 在线段AB上，四边形ACDE 和四边形CBFG 都是正方形. 设BC=x. (1) AC＝_________.
(2)设正方形ACDE 和正方形CBFG 的总面积 为S， 用x 表示S 的函数表达式为S＝_______________.(3)总面积S 有最大值还是最小值？这个最大值或 最小值是多少?(4)当总面积S 取最大值或最小值时，点C 在AB 的 什么位置？
(3)S＝2x 2－4x＋4＝2(x－1)2＋2. ∵a＝2＞0，∴S 有最小值，S最小值＝2.(4)当S＝2时，2(x－1)2＋2＝2，解得x＝1. ∵AB＝2，AC＝2－x＝1，∴点C 在AB 的中点处．
2 已知一个直角三角形两直角边长之和为20 cm，则 这个直角三角形的最大面积为(　　) A．25 cm2 B．50 cm2 C．100 cm2 D．不确定3 用一条长为40 cm的绳子围成一个面积为a cm2的长 方形，a 的值不可能为(　　) A．20 B．40 C．100 D．120
4 如图，在矩形ABCD 中，AD＝1，AB＝2，从较短边AD上找一点E，过这点剪下两个正方形，它们的边长分别是AE，DE，当剪下的两个正方形的面积之和最小时，点E 应选在(　　) A．AD 的中点 　　　 B．AE∶ED＝( －1)∶2 C．AE∶ED＝ ∶1 　　　 D．AE∶ED＝( －1)∶2
如图，在Rt△ABC 中，∠C＝90°，AC＝6 cm，BC＝2 cm，点P 在边AC上，从点A 向点C 移动，点Q 在边CB上，从点C向点B 移动．若点P，Q 均以1 cm/s的速度同时出发，且当一点移动到终点时, 另一点也随之停止，连接PQ，则线段PQ的最小值是(　　)A．20 cm B．18 cm C．2 cm D．3 cm
在一空旷场地上设计一落地为矩形ABCD 的小屋，AB＋BC＝10 m，拴住小狗的10 m长的绳子一端固定在B点处，小狗在不能进入小屋内的条件下活动，其可以活动的区域面积为S (m2)．(1)如图①，若BC＝4 m， 则S＝________；
(2)如图②，现考虑在(1)中矩形ABCD 小屋的右侧以CD 为边拓展一等边三角形CDE 区域，使之变成落地为五边形ABCED 的小屋，其他条件不变，则在BC 的变化过程中，当S 取得最小值时，边BC 的长为________．
某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙(墙足够长)，已知计划中的建筑材料可建围墙的总长为50 m．设饲养室长为x (m)，占地面积为y (m2)．(1)如图①，问当饲养室长x 为多少时，占地面积y 最大？(2)如图②，现要求在图中所示位 置留2 m宽的门，且仍使饲养室 的占地面积最大，小敏说：“只 要饲养室长比(1)中的长多2 m就 行了．”请你通过计算，判断小 敏的说法是否正确．
(1)∵ y＝x · ＝－ (x－25)2＋ ， ∴当x＝25时，占地面积y最大， 即当饲养室长为25 m时，占地面积最大．(2)∵y ＝x · ＝－ (x－26)2＋338， ∴当x＝26时，占地面积 y 最大， 即当饲养室长为26 m时，占地面积最大． ∵26－25＝1≠2， ∴小敏的说法不正确．
工人师傅用一块长为10 dm，宽为6 dm的矩形铁皮制作一个无盖 的长方体容器，需要将四角各裁掉一个正方形．(厚度不计) (1)在图中画出裁剪示意图，用实线表示 裁剪线，虚线表示折痕；并求长方体 底面面积为12 dm2时，裁掉的正方形 边长多大？ (2)若要求制作的长方体的底面长不大于底面宽的五倍， 并将容器进行防锈处理，侧面每平方分米的费用为 0.5元，底面每平方分米的费用为2元，裁掉的正方 形边长多大时，总费用最低，最低为多少？
(1)如图： 设裁掉的正方形边长为x dm， 由题意可得(10－2x )(6－2x )＝12， 即x 2－8x＋12＝0，解得x＝2或x＝6(舍去)． 答：裁掉的正方形的边长为2 dm.(2)∵长不大于宽的五倍，∴10－2x≤5(6－2x )，解得x ≤2.5， 又∵x ＞0，∴0＜x≤2.5. 设总费用为w 元，由题意可知w＝0.5×2x (16－4x )＋2(10－ 2x )(6－2x )＝4x 2－48x＋120＝4(x－6)2－24， ∴当0＜x≤2.5时，w 随x 的增大而减小， ∴当x＝2.5时，w 有最小值，最小值为25. 答：当裁掉边长为2.5 dm的正方形时，总费用最低，最低 费用为25元．
如图，在△ABC 中，∠B＝90°，AB＝12 mm，BC＝24 mm，动点 P 从点A 开始沿边AB 向B 以2 mm/s的速度移动，动点Q 从点B 开 始沿边BC 向C 以4 mm/s 的速度移动．已知P，Q 分别从A，B 同 时出发，求△PBQ 的面积S (mm2)与出发时间t (s)的函数表达式，并 求出t 为何值时，△PBQ 的面积最大，最大值是多少？
如图①，为美化校园环境，某校计划在一块长为60 m，宽为40 m 的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修 建成同样宽的通道，设通道宽为a m. (1)用含a 的式子表示花圃的面积． (2)如果通道所占面积是整个长方 形空地面积的 ，求出此时通道的宽． (3)已知某园林公司修建通道、花圃的造价y1(元)，y2(元) 与修建面积x (m 2)之间的函数关系如图②所示，如果学 校决定由该公司承建此项目，并要求修建的通道的宽 度不少于2 m且不超过10 m，那么通道宽为多少时，修 建的通道和花圃的总造价最低？最低总造价为多少元？
(1)由题可知花圃的面积为(60－2a)(40－2a)＝ 4a 2－200a＋2 400(m2)．(2)通道的面积为60×40－(4a 2－200a＋2 400)＝ －4a 2＋200a (m2)， ∴－4a 2＋200a＝ ×2 400. ∴4a 2－200a＋900＝0. 解得a＝5或a＝45(舍去)． ∴通道的宽为5 m.
利用二次函数求几何图形面积的最值是二次函数应用的重点之一，解决此类问题的基本方法是：借助已知条件，分析几何图形的性质，确定二次函数表达式，再根据二次函数的图象和性质求出最值，从而解决问题．