




数学九年级下册第32章 投影与视图32.3 直棱柱和圆锥的侧面展开图精品课件ppt
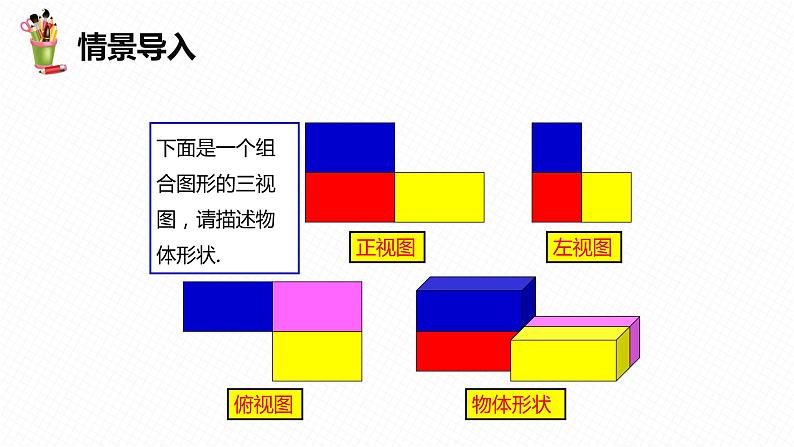
展开下面是一个组合图形的三视图,请描述物体形状.
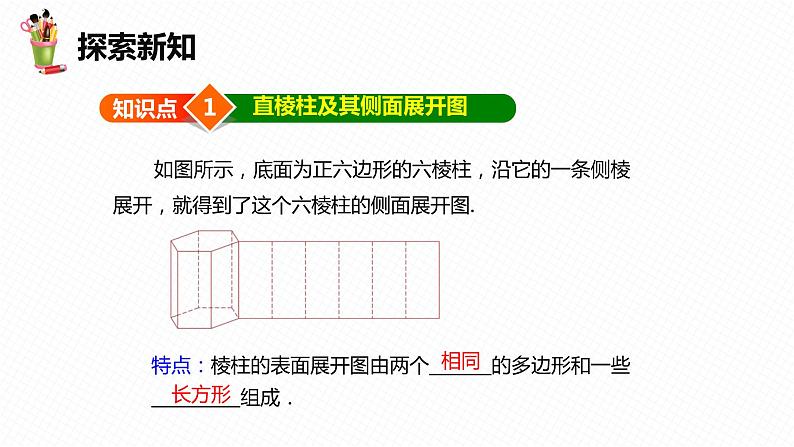
如图所示,底面为正六边形的六棱柱,沿它的一条侧棱展开,就得到了这个六棱柱的侧面展开图.
特点:棱柱的表面展开图由两个_______的多边形和一些__________组成.
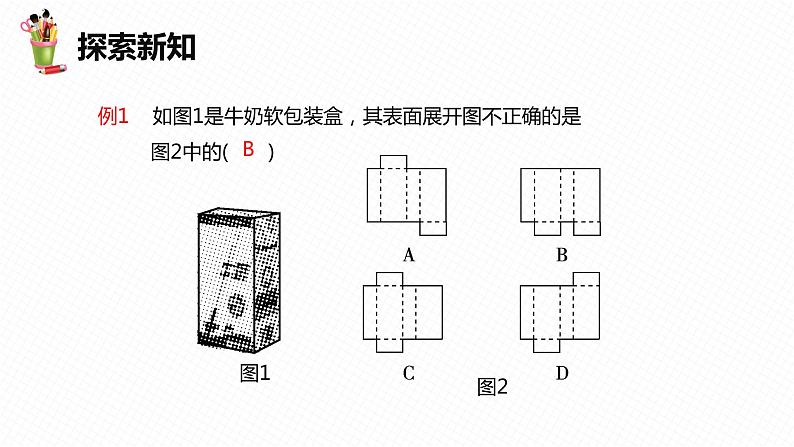
例1 如图1是牛奶软包装盒,其表面展开图不正确的是 图2中的( )
根据包装盒的形状可以发现,选项B中的对应位置有误;另外本题也可以把选项中的表面展开图进行折叠,看是否符合题意,通过折叠可以发现B是不正确的.
本题利用了转化思想,由几何体通过空间想象得到其表面展开图,所得的表面展开图要符合实际情况.
例2 如图所示为一个正方体. 按棱画出它的一种表面展开图.
按棱展开的方式有多种,其中一种如图所示.
如图所示的四个图形都是由立体图形展开得到的,相应的立体图形依次是( )A.正方体、圆柱、三棱柱、圆锥B.正方体、圆锥、三棱柱、圆柱C.正方体、圆柱、三棱锥、圆锥D.正方体、圆柱、四棱柱、圆锥
把如图所示的三棱柱展开,所得到的展开图是( )
如图,圆柱体的表面展开后得到的平面图形是( )
下列图形经过折叠不能围成棱柱的是( )
将如图所示的表面带有图案的正方体沿某些棱展开后,得到的图形是( )
圆锥的表面展开图: 将圆锥的侧面沿它的一条母线剪开,会得到圆锥的侧面展开图为扇形,其半径等于母线长,弧长是底面圆的周长.
如图,一个圆锥的高为3 cm,侧面展开图是半圆.求:(1)圆锥的母线长与底面半径之比;(2)∠BAC 的度数;(3)圆锥的侧面积(结果保留π).
(1)题直接根据圆锥的侧面展开图(扇形)的弧长等于 圆锥底面周长可得比值;(3)题根据圆锥的侧面积是侧面展开图(扇形)的面积, 直接利用公式解题即可.(1)设此圆锥的高为h,底面半径为r, 母线长AC=l,易知2πr=πl, ∴l∶r=2∶1.
(2)连接AO,则AO⊥OC,由(1)知 =2, ∴圆锥高与母线的夹角为30°,∴∠BAC=60°.(3)由图可知l 2=h 2+r 2,又∵h=3 cm, ∴(2r )2=(3 )2+r 2,即4r 2=27+r 2, 解得r=3 cm,∴l=2r=6 cm, ∴圆锥的侧面积为 =18π(cm2).
本题运用了方程思想和数形结合思想,从而使问题得以转化,注意圆锥底面半径的确定.
有一圆锥,它的高为8 cm,底面半径为6 cm,则这个圆锥的侧面积是________ cm2. (结果保留π)如图所示,沿一条母线将圆锥侧面剪开并展平,得到一个扇形.若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,则该圆锥的母线长l 为________cm.
如图,圆锥的侧面展开图是半径为3,圆心角为90°的扇形,则该圆锥的底面周长为( )A. B. C. D.
将一边长为2的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则三棱锥四个面中最小的面的面积是( )A.1 B. C. D.
如图所示的是一多面体的表面展开图,每个面上都标注了字母,请回答:如果F 面在前面,从左面看是B 面,那么哪一面会在上面?
易错点:将表面展开图折成立体图形时出错.
错解:C 面会在上面.诊断:将表面展开图折成立体图形时,分向里折和向外 折两种情况,错解中忽略了一种情况,因此造成 漏解.正解:E 面或C 面会在上面.
如图是一个几何体的三视图,则这个几何体的侧面积是( )A.12π cm2 B.8π cm2 C.6π cm2 D.3π cm2
一个几何体的三视图如图所示,其中主视图和左视图都是腰长为4,底边长为2的等腰三角形,则这个几何体侧面展开图的面积为( )A.2π B. π C.4π D.8π
如图①所示的正方体木块棱长为6 cm,沿其相邻三个面的 对角线(图中虚线)截掉一角,得到如图②所示的几何体,一 只蚂蚁沿着图②所示的几何体表面从顶点A 爬行到顶点B 的 最短距离为_______________cm.
如图,有一直径是米的圆形铁皮,现从中剪出一个圆周 角是90°的最大扇形ABC,则: (1)AB 的长为________米; (2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆 的半径为________米.
如图所示的是一个长方体形状的仓库示意图,其中AB=8 m, BC=6 m,BF=5 m.M 为AB上的一点,N 为GF上的一点, 且AM= AB,GN= GF. 如果在M 点有一只壁虎,N 点有 一只蚊子,则壁虎爬到蚊子处的最短距离为多少米?
6 如图所示的是一个几何体的三视图. (1)写出这个几何体的名称; (2)根据图中所示数据计算这个几何体的表面积; (3)如果一只蚂蚁要从这个几何体中的点B 出发,沿表面爬到 AC 的中点D,请你求出这条路线的最短路程.
(1)∵主视图以及左视图都是三角形,俯视图为圆及圆心, ∴该几何体是圆锥.(2)S表=S侧+S圆=πrl+πr 2=12π+4π=16π(平方厘米).(3)如图将圆锥侧面展开,得到扇形ABB ′,连AC,BD,经分析 可知线段BD 为所求的最短路线.设∠BAB ′=n°. ∵ =4π,∴n=120,即∠BAB ′=120°. ∵C 为弧BB ′中点,∴∠BAD=60°. 连接BC,则△ABC 为等边三角形, 又∵D 为AC 的中点,∴BD⊥AC, ∴△ABD 为直角三角形,∴BD=AB · sin∠BAD=6× =3 (厘米).即所求路线的最短路程为3 厘米.
常见图形的侧面展开图:圆锥的侧面展开图是一个扇形;圆柱的侧面展开图是矩形;正方体的表面展开图有11种情况;棱柱的侧面展开图是矩形.
冀教版九年级下册32.3 直棱柱和圆锥的侧面展开图授课ppt课件: 这是一份冀教版九年级下册32.3 直棱柱和圆锥的侧面展开图授课ppt课件,共22页。PPT课件主要包含了圆锥的侧面积计算公式,和4的矩形,πcm2,解得n60,∴2π,∴BBAB6等内容,欢迎下载使用。
冀教版九年级下册第32章 投影与视图32.3 直棱柱和圆锥的侧面展开图优质课课件ppt: 这是一份冀教版九年级下册第32章 投影与视图32.3 直棱柱和圆锥的侧面展开图优质课课件ppt,共21页。PPT课件主要包含了从生活中来,创设情景,新课导入,新课讲解,观察与思考,形成概念,底面图形边数,相应的立方体的名称,直三棱柱,直四棱柱等内容,欢迎下载使用。
初中数学冀教版九年级下册32.3 直棱柱和圆锥的侧面展开图集体备课ppt课件: 这是一份初中数学冀教版九年级下册32.3 直棱柱和圆锥的侧面展开图集体备课ppt课件,共22页。PPT课件主要包含了学习目标,冀教版九下,一起探究,三棱柱,四棱柱,五棱柱,三棱柱的侧面由,个矩形组成,四棱柱的侧面由,五棱柱的侧面由等内容,欢迎下载使用。













