27.2 相似三角形 第三课时-九年级数学下册课件（人教版）

这是一份27.2 相似三角形 第三课时-九年级数学下册课件（人教版），共40页。

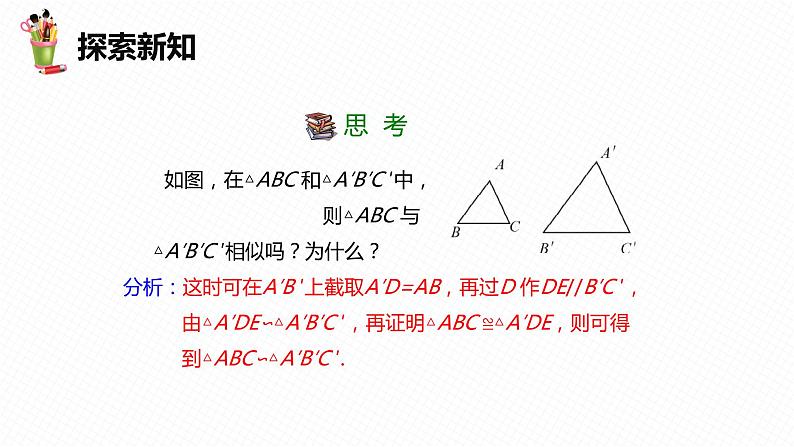
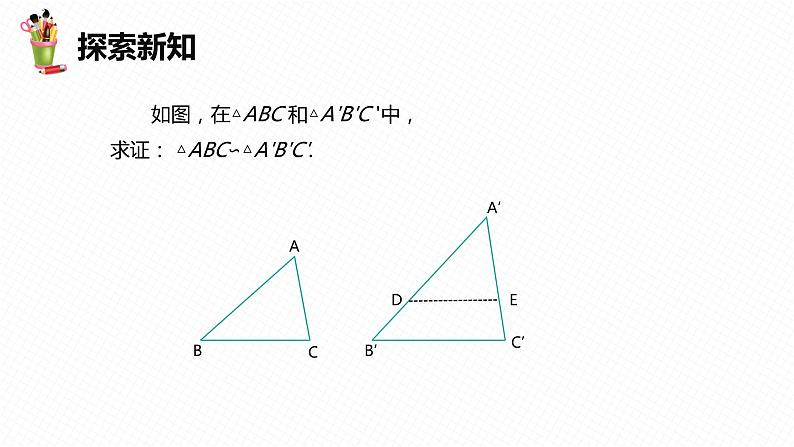
27.2 相似三角形第3课时目录课前导入新课精讲学以致用课堂小结课前导入情景导入判定两个三角形全等我们有SSS 的方法，类似地，判定两个三角形相似是否也有类似的简单方法呢？新课精讲探索新知1知识点三边成比例的两个三角形相似任意画一个三角形，再画另一个三角形，使它的各边长都是原来各边长的2倍，度量这两个三角形的对应角，他们对应相等吗？这两个三角形全等吗？ 问 题探索新知如图，在△ABC 和△A′B′C ′中， 则△ABC 与 △A′B′C ′相似吗？为什么？分析：这时可在A′B ′上截取A′D=AB，再过D 作DE//B′C ′，由△A′DE∽△A′B′C ′，再证明△ABC ≌△A′DE，则可得到△ABC∽△A′B′C ′.思 考探索新知如图，在△ABC 和△A'B'C '中，求证： △ABC∽△A'B'C'. 探索新知证明：在线段A′B ′（或它的延长线）上截取A′D=AB，过点D作 DE//B′C ′，交A′C ′于点E.根据前面的定理，可得△A′DE∽△A'B'C'. ∴DE=BC，A′E=AC.∴ △A′DE ≌ △ABC. ∴△ABC ∽△A'B'C'.△A′DE 是证明的中介，它把△ABC 与△A′B′C′ 联系起来.探索新知由此我们得到利用三边判定三角形相似的定理（如图）：三边成比例的两个三角形相似.△ABC ∽△A'B'C '探索新知例1 根据下列条件，判断△ABC 与△A'B'C' 是否相似，并说明理由：AB=4 cm，BC=6 cm，AC=8 cm，A′B ′= 12 cm，B′C ′= 18 cm，A′C ′=24 cm. 解：∴△ABC ∽△A'B'C'.探索新知这个判定三角形相似的方法与三角形全等的判定方法“边边边”十分相似，所不同的是在相似的判定方法中的 “三边”要求的是“比相等”. 三边的对应关系是“短∶短”“中∶中”“长∶长”.典题精讲根据下列条件，判断△ABC 与△A′B′C ′是否相似，并说明理由:AB= 10 cm，BC = 8 cm，AC = 16 cm,A′B ′= 16 cm，B′C ′= 12. 8 cm，A′C ′= 25. 6 cm.解：相似 ∴△ABC∽△A′B′C ′.典题精讲图中的两个三角形是否相似？为什么？相似理由如下：∵∴两个三角形的三边成比例．∴这两个三角形相似．解：典题精讲要制作两个形状相同的三角形框架，其中一个三角形框架的三边长分别为 4 cm，5 cm和6 cm，另一个三角形框架的一边长为2 cm，它的另外两条边长应当是多少？你有几种制作方案？设另外两条边长分别是x cm和y cm(x