




初中数学人教版九年级下册27.3 位似完美版ppt课件
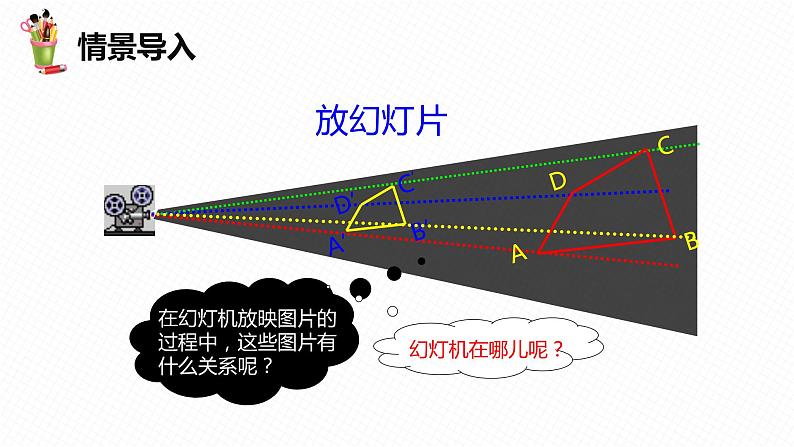
展开在幻灯机放映图片的过程中,这些图片有什么关系呢?
这两个图形有哪些特征呢?
2.每组对应点所在直线都经过同一点;
3. 对应边互相平行.
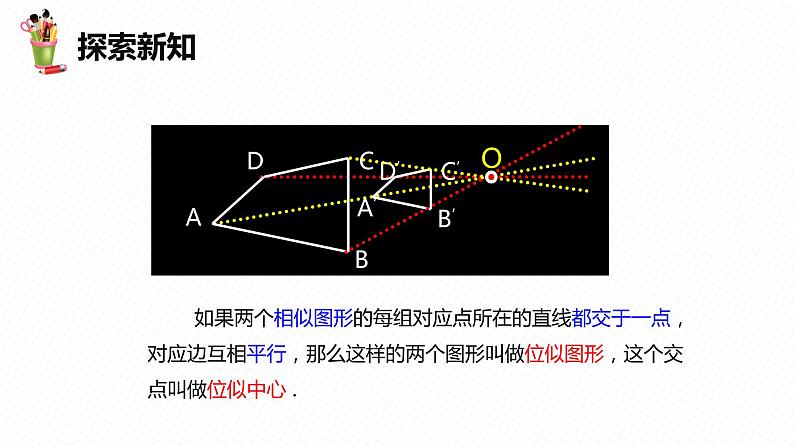
如果两个相似图形的每组对应点所在的直线都交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个交点叫做位似中心 .
同时满足下面三个条件的两个图形才叫做位似图形.三条件缺一不可.
显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.
例1 判断如图所示的各图中的两个图形是否是位似图形, 如果是,请指出其位似中心.解:(1)是位似图形,位似中心为点A; (2)是位似图形,位似中心为点P; (3)不是位似图形; (4)是位似图形,位似中心为点O; (5)不是位似图形.
如图所示两个四边形是位似图形,它们的位似中心是( ) A.点M B.点N C.点O D.点P
对于平面图形上的任意两点P,Q,如果经过某种变换得到新图形上的对应点P ′,Q ′,保持PQ=P′Q ′,我们把这种变换称为“等距变换”,下列变换中不一定是等距变换的是( )A.平移 B.旋转 C.轴对称 D.位似
利用位似图形将一个图形放大或缩小时,首先要选取一点作为位似中心,那么位似中心可以在( )A.图形外 B.图形内 C.图形上 D.以上都可以
图中有多边形相似吗?如果有,那么这种相似有什么特征?
位似图形上任意一对对应点到位似中心的距离之比等于位似比.
1. 位似图形的对应点和位似中心在同一条直线上;
例2 △ABC 与△A′B ′C ′是位似图形,且△ABC 与△A′B ′C ′的位似比 是1∶2,已知△ABC 的面积是3,则△A′B ′C ′的面积是( ) A. 3 B. 6 C. 9 D. 12导引:∵△ABC 与△A′B ′C ′是位似图形,且△ABC 与 △A′B ′C ′的位似比是1∶2, ∴△ABC 与△A′B ′C ′相似,且相似比为1∶2. ∴△ABC 与△A′B ′C ′的面积比为1∶4. ∵△ABC 的面积是3,∴△A′B ′C ′的面积是12.
两个图形位似,则两个图形相似,所以相似图形的性质,位似图形都满足,可以直接运用.
如图,△OAB 和△OCD 是位似图形,AB 与CD 平行吗?为什么?
解:AB∥CD. 理由如下: ∵△OAB 和△OCD 是位似图形, ∴△OAB∽△OCD. ∴∠OAB=∠C. ∴AB∥CD.
下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于相似比.其中正确命题的序号是( )A.②③ B.①② C.③④ D.②③④
如图,△A′B′C ′是△ABC 以点O 为位似中心经过位似变换得到的,若△A′B′C ′的面积与△ABC 的面积比是4∶9,则OB ′∶OB 为( )A.2∶3 B.3∶2 C.4∶5 D.4∶9
探究: 如果在四边形ABCD 外任取一点O,分别在OA,QB,OC,OD 的反向延长线上取点A′ ,B ′ ,C ′ ,D ′ ,使得四边形A′B ′C ′D ′ 与四边形ABCD 有什么关系?如果点O 取在四边形ABCD 内部呢? 分别画出得到的四边形A′B ′C ′D ′ .
例如,要把四边形ABCD 缩小到原来的 以在四边形ABCD 外任取一点O(如图),分别在线段OA,OB,OC,OD上取点A′ ,B ′ ,C ′ ,D ′ ,使得 顺次连接点A′ ,B ′ ,C ′ ,D ′, 所得四边形A′B ′C ′D ′就是所要求的图形 .
画位似多边形的一般步骤:(1)确定位似中心; (2)分别连接位似中心和能代 表原多边形的关键点; (3)根据位似比,利用截取的方法,找出所作的位似 多边形的对应点;(4)顺次连接上述各点,得到放大或缩小的多边形.
例3 如图,在6×8网格图中,每个小正方形边长均为1,点O 和 △ABC 的顶点均为小正方形的顶点. (1)以O 为位似中心,在网格图中作△A′B ′C ′,使△A′B ′C ′和 △ABC 位似,且位似比为 1∶2; (2) 连接(1)中的AA′,求四边形AA′C ′C 的周长.(结果保留根号)
分析:(1)根据位似比是1∶2,画出以O 为位似中心的△A′B ′C ′; (2)根据勾股定理求出AC,A′C ′的长,由于AA′,CC ′的 长易得,相加即可求得四边形AA′C ′C 的周长.解:(1)如图所示: (2)AA′=CC ′=2. 在Rt△OA′C ′中, OA′=OC ′=2,得A′C ′= 同理可得AC= ∴四边形AA′C′C的周长=
如图,以点O 为位似中心,将△ ABC 放大为原来的3倍.
解:如图所示的△A′B′C ′或△A″B″C ″就是所要求作的三角形.
如图是△ABC 位似图形的几种画法,其中正确的有( ) A.1个 B.2个 C.3个 D.4个
如图,正方形网格中有一条简笔画“鱼”,请你以点D 为位似中心将其放大,使新图形与原图形的对应线段的比是2∶1,画出符合条件的所有图形.(不要求写作法)
易错点:对位似变换时图形的位置考虑不全而漏解.
易错总结:此题易忽略其中一种情况,当题中对位似图形 的位置没有限制条件时,一定要考虑全面.
如图,点O 是五边形ABCDE 和五边形A1B1C1D1E1的位似中心,若OA:OA1=1:3,则C1D1:CD=( )A.1:2 B.1:3 C.3:1 D.1:4
如图,△ABC 与△DEF 是位似图形,点O 是位似中心,相似比是1:2,已知DE=4,则AB 的长是( )A.2 B.4 C.8 D.1
如图,在10×10的正方形网格中,点A,B,C,D 均在格点上,以点A 为位似中心画四边形AB′C′D′,使它与四边形ABCD 位似,且相似比为2.(1)在图中画出四边形AB′C′D ′;(2)填空:△AC′D ′是__________ 三角形.
4 如图,▱ABCD 的对角线AC,BD 相交于点O,点E,F, G,H 分别是线段OA,OB,OC,OD 的中点,那么 ▱ABCD 与四边形EFGH 是否是位似图形?为什么?
如图,△ABC 与△A′B ′C ′是位似图形,点A,B,A′,B ′, O 共线,点O 为位似中心. (1)AC 与A′C ′平行吗?为什么? (2)若AB=2A′B ′,OC ′=5,求CC ′的长.
(1)AC∥A′C ′.理由如下:∵△ABC 与△A′B ′C ′是位似图形, ∴△ABC∽△A′B ′C ′. ∴∠A=∠C ′A′B ′. ∴AC∥A′C ′.(2)由(1)知△ABC∽△A′B ′C ′, ∴ . ∵AB=2A′B ′,∴ . 又∵△ABC 与△A′B ′C ′是位似图形, ∴ ∵OC ′=5,∴OC=10. ∴CC ′=OC-OC ′=10-5=5.
如图,已知△DEO 与△ABO 是位似图形,△OEF 与△OBC 是位似图形. 求证:OD ·OC=OF ·OA.
如图,在6×8的网格图中,每个小正方形的边长均为1, 点O 和△ABC 的顶点均在小正方形的顶点上. (1)以O 为位似中心,在网格图中作△A′B ′C ′和△ABC 位似,且相似比为1∶2; (2)连接(1)中的AA′,求四边形AA′C ′C 的周长(结果保 留根号).
(1)如图.(2)如图,四边形AA′C ′C 的周长为AA′+A′C ′+CC ′+AC=2+2 +2+4 =4+6 .
8 如图,在矩形ABCD 中,对角线AC,BD 相交于点O. (1)过点O 作OE⊥BC 于点E,连接DE 交OC 于点F,作 FG⊥BC 于点G,则△ABC 和△FGC 是位似图形吗? 若是,请写出位似中心,并求出相似比;若不是, 请说明理由. (2)连接DG 交OC 于点H,作HI⊥BC 于点I,试确定CI∶BC的值(直接写出结果).
(1)△ABC 与△FGC 是位似图形,位似中心是点C, 在矩形ABCD 中,AD∥BC,∴△AFD∽△CFE. ∴ . 又∵AD=BC,∴ . ∵∠ABC=90°,OE⊥BC,∴OE∥AB. 又∵OA=OC,∴CE=BC, ∴ . ∴ , 即△ABC 与△FGC 的相似比为3∶1.(2)CI∶BC=1∶4.
如图,某小区原有一矩形花坛,现对小区进行规划,按要求作出相应的位似图形. (1)在原地将花坛扩建,使各边的对应边为原来的3倍; (2)在异地修建一块矩形草坪,使它与花坛的对应边的比为4∶1, 你能设计出图纸吗?
2.位似图形的性质 位似图形的对应点和位似中心在同一条直线上,它们到位 似中心的距离之比等于相似比. (位似比)
如果两个相似图形的每组对应点所在的直线都交于一点,对应边互相平行,那么这样的两个图形叫做位似图形, 这个交点叫做位似中心 .
人教版九年级下册27.3 位似教学课件ppt: 这是一份人教版九年级下册27.3 位似教学课件ppt,共20页。PPT课件主要包含了圆的定义,有关概念,半径直径,圆心角定理,弧长计算公式,圆的基本性质,弦弦心距,圆周角,圆的轴对称性,圆周角定理等内容,欢迎下载使用。
数学九年级下册27.3 位似授课ppt课件: 这是一份数学九年级下册27.3 位似授课ppt课件,共20页。PPT课件主要包含了位似图形的定义,位似多边形的定义,位似的特征等内容,欢迎下载使用。
初中数学第二十七章 相似27.3 位似集体备课课件ppt: 这是一份初中数学第二十七章 相似27.3 位似集体备课课件ppt,文件包含273位似课时1pptx、273位似课时2pptx等2份课件配套教学资源,其中PPT共61页, 欢迎下载使用。













