初中数学29.1 投影精品ppt课件

这是一份初中数学29.1 投影精品ppt课件，共43页。PPT课件主要包含了课前导入，新课精讲，学以致用，课堂小结，情景导入，探索新知，知识点，正投影的定义，典题精讲，平行投影等内容，欢迎下载使用。

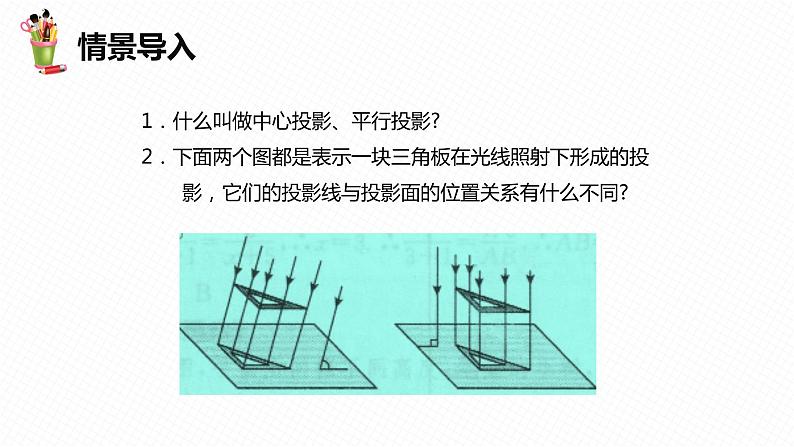
1．什么叫做中心投影、平行投影?2．下面两个图都是表示一块三角板在光线照射下形成的投 影，它们的投影线与投影面的位置关系有什么不同?
正投影法：投影线与投影面垂直的平行投影法，所得的投影，称为正投影 .
例1 如图所示的圆台的上下底面与投影线平行，圆台 的正投影是（　　） A、矩形 B、两条线段 C、等腰梯形 D、圆环 根据正投影的定义及正投影形状分析．根据题意： 圆台的上下底面与投影线平行，则圆台的正投影是 该圆台的轴截面，即等腰梯形．故选C．
物体的正投影的形状、大小与物体相对于投影面的位置有关．它分物体与投影面平行、倾斜、垂直三种情况.
如图，投影线的方向如箭头所示，画出圆柱体的 正投影
解：(1)如图所示；(2)如图所示．
2 投影线________于投影面产生的投影叫做正投影；它包含以下两个要素： (1)正投影是特殊的 ，它不可能是 ． (2)正投影只要求________与________垂直，与物体位 置无关．
球的正投影是(　　)A．圆 B．椭圆 C．点 D．圆环正方形的正投影不可能是(　　)A．线段 B．矩形 C．正方形 D．梯形
下列投影中，正投影有(　　) A．0个　　B．1个　　C．2个　　D．3个
6 如图，水杯的杯口与投影面平行，投影线的方向 如箭头所示，它的正投影是(　　)
底面与投影面垂直的圆锥体的正投影是(　　)A．圆 B．三角形 C．矩形 D．正方形
把一个正六棱柱如图摆放，光线由上向下照射此正六棱柱时的正投影是(　　)
如图，投影线的方向如箭头所示，画出下列各图形的正投影．
如图,把一根直的细铁丝(记为线段AB )放在三个不同位置： (1) 铁丝平行于投影面；(2) 铁丝倾斜于投影面；(3) 铁丝垂直于投影面（铁丝不一定要与投影面有交点）.三种情形下铁丝的正投影各是什么形状?
通过观察、测量可知：(1)当线段AB 平行于投影面时，它的正投影是线段A1B1， 它们的大小关系为AB=A1B1 ； (2)当线段AB 倾斜于投影面时，它的正投影是线段A2B2， 它们的大小关系为AB＞A2B2 ；(3)当线段AB 垂直于投影面时，它的正投影是一个点A3.
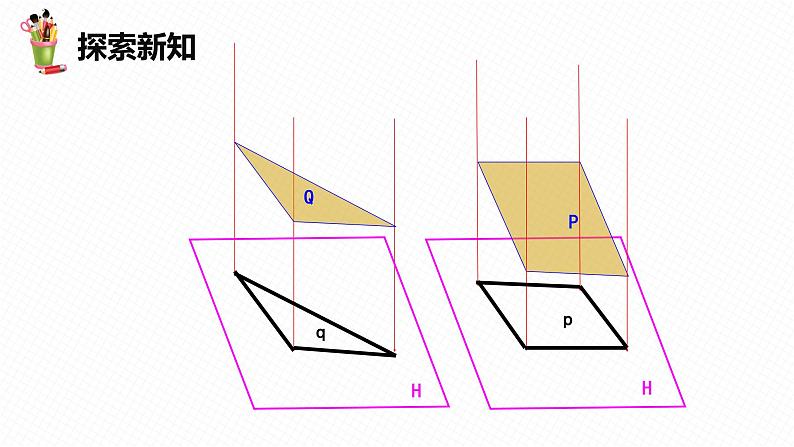
如图，把一块正方形硬纸板P (记为正方形ABCD )放在三个不同位置：(1) 纸板平行于投影面； (2) 纸板倾斜于投影面；(3) 纸板垂直于投影面.三种情形下纸板的正投影各是什么形状?
通过观察、测量可知：当纸板P 平行于投影面时，P 的正投影与P 的形状、大小一样；当纸板P 倾斜于投影面时，P 的正投影与P 的形状、大小不完全 一样；(3) 当纸板P 垂直于投影面时，P 的正投影成为一条线段.
当物体的某个面平行于投影面时，这个面的正投影与这个面的形状、 大小完全相同.
例2 画出如图摆放的正方体在投影面 上的正投影. (1) 正方体的一个面ABCD 平行于投影面 (图(1)); (2) 正方体的一个面ABCD 倾斜于投影面， 底面ADEF 垂直于投 影面，并且其对角线AE 垂直于投影面(图(2) )
(1)当正方体在如图 (1)的位置时，正方体的一个面ABCD 及与其相对的另一面与投影面平行，这两个面的正投影是与正方体的一个面的形状、大小完全相同的正方A′B′C′D′.正方形A′B′C′D′ 的四条边分别是正方体其余四个面（这些面垂直于投影面）的投影.因此，正方体的正投影是一个正方形.
(2)当正方体在如图 (2)的位置时，它的面ABCD 和面ABGF 倾斜于投影面，它们的投影分别是矩形A′B′C′D′ 和A′B′G′F′ ；正方体其余两个侧面的投影也分别是上述矩形；上、下底面的投影分别是线段D′F′和C′G′.因此，正方体的投影是矩形F′G′C′D′ 其中线段A′B′ 把矩形一分为二.
(1)如图 (1)，正方体的正投影为正方形A′B′C′D′ ， 它与正方体的一个面是全等关系.(2)如图(2)，正方体的正投影为矩形F′G′C′D′ ，这个 矩形的长等于正方体的底面对角线长，矩形的宽 等于正方体的棱长.矩形上、下两边中点连线A′B′ 是正方体的侧棱AB 及它所对的另一条侧棱EH 的 投影.
物体的正投影的形状、大小与物体相对于投影面的位置有关．画一般立体图形的正投影的关键是找出平行于投影面的立体图形的最大截面．
一根笔直的小木棒(记为线段AB )，它的正投影为线段CD，则下列各式中一定成立的是(　　)A．AB＝CD B．AB≤CDC．AB＞CD D．AB≥CD
小乐用一块矩形硬纸板在阳光下做投影实验，通过观察，发现这块矩形硬纸板在平整的地面上不可能出现的投影是(　　) A．三角形 B．线段 C．矩形 D．平行四边形
当棱长为20 cm的正方体的某个面平行于投影面时，这个正方体的正投影的面积为(　　)A．200 cm2　 B．300 cm2　C．400 cm2　 D．600 cm2
如图所示，把正方体一个顶点朝上立放，在它下面放一张白纸，使纸面与太阳光垂直，则正方体在纸上的正投影是(　　)
易错点：对正方体的正投影的类型认识不全而致错.
几何体在平面P 的正投影，取决于(　　)①几何体的形状；②投影面与几何体的位置关系；③投影面P 的大小．A．①②　 　B．①③　　C．②③　 　D．①②③
已知一根长为8 cm的木棒AB 与投影面平行，投影线垂直于投影面． (1)求此时的影子A1B1的长度； (2)如图是将木棒绕其端点A 逆时针旋转30°后的示意图(此时平面ABB2A2垂直于投影面)，求旋转后木棒的影子A2B2的长
(1)当木棒平行于投影面时，其正投影的长度与木棒的长度一致；(2)当木棒倾斜于投影面时，可转化为解直角三角形来求解．
(1)因为木棒平行于投影面， 所以A1B1＝AB＝8 cm， 即此时的影子A1B1的长度为8 cm.(2)过点A作AH⊥BB2于点H. 因为AA2⊥A2B2，BB2⊥A2B2， 所以四边形AA2B2H 为矩形， 所以AH＝A2B2. 在Rt△ABH 中，∠BAH＝30°，AB＝8 cm， 所以A2B2＝AH＝AB·cs 30°＝8× ＝4 (cm)． 即旋转后木棒的影子A2B2的长为4 cm.
已知一纸板的形状为正方形ABCD，且边长为10 cm.如图，四边形A1B1C1D1是正方形ABCD 在面β 上的正投影，AD，BC 与投影面β 平行，且AB，CD 与投影面β 成30°角，求正方形ABCD 的正投影的面积．
过点A作AH⊥BB1于点H.依题意，得∠BAH＝30°，四边形A1B1C1D1是矩形，其中A1D1＝AD，A1B1＝AH.∵AH⊥BB1，∠BAH＝30°，∴AH＝AB·cs 30°＝10× ＝5 (cm)，∴A1B1＝AH＝5 cm.∵A1D1＝AD＝10 cm，∴S四边形A1B1C1D1＝A1B1·A1D1＝5 ×10＝50 (cm2)．则正方形ABCD的正投影的面积是50 cm2.
规律总结：求投影的面积，先确定投影的形状，再根据相应的面积公 式，有针对性地求出相关线段的长.
一个圆锥的轴截面平行于投影面，圆锥的正投影是 等腰三角形，如图所示，等腰三角形的腰长为13 cm， 高为12 cm，求该圆锥的体积及表面积． (提示：V圆锥＝ πr 2h，其中r 是底面圆的半径，h 是 圆锥的高)
由于圆锥的轴截面平行于投影面，其正投影是等腰三角形，因此圆锥的高等于等腰三角形的高；圆锥底面圆的半径等于等腰三角形底边长的一半．如图，作AD⊥BC 于D，AB＝AC＝13 cm，AD＝12 cm，∴CD＝5 cm，∴r＝CD＝5 cm，h＝12 cm.∴V圆锥＝ πr2h＝100π cm3，底面周长为l＝2πr＝10π cm，R＝AC＝13 cm，S表＝ lR＋πr2＝90π cm2.
操作与研究： 如图，△ABC 被平行光线照射，CD⊥AB 于D，AB 在 投影面上． (1)指出图中AC 的投影是什么，CD 与BC 的投影呢？ (2)探究：当△ABC 为直角三角形(∠ACB＝90°)时， 易得AC 2＝AD ·AB，此时有如下结论：直角三角形 一直角边的平方等于它在斜边上的射影与斜边的乘 积，这一结论我们称为射影定理． 通过上述结论的推理，请证明 以下两个结论： ①BC 2＝BD ·AB；②CD 2＝AD ·BD.
(1)解：AC 的投影是AD，CD 的投影是点D，BC 的投影是BD.(2)证明：①易证得△BCD∽△BAC， 可得BC 2＝BD ·AB； ②易证得△ACD∽△CBD， 可得CD 2＝AD ·BD.
1.回顾正投影的含义及其性质；2.反思作简单几何图形的正投影的过程及自己作图过 程中失误的原因，体会正投影的作图方法与技巧；3.物体的正投影的形状、大小与它相对于投影面的位 置是否有关系？