高中数学北师大版 (2019)必修 第一册3 函数的单调性和最值课时作业

这是一份高中数学北师大版 (2019)必修 第一册3 函数的单调性和最值课时作业，共11页。
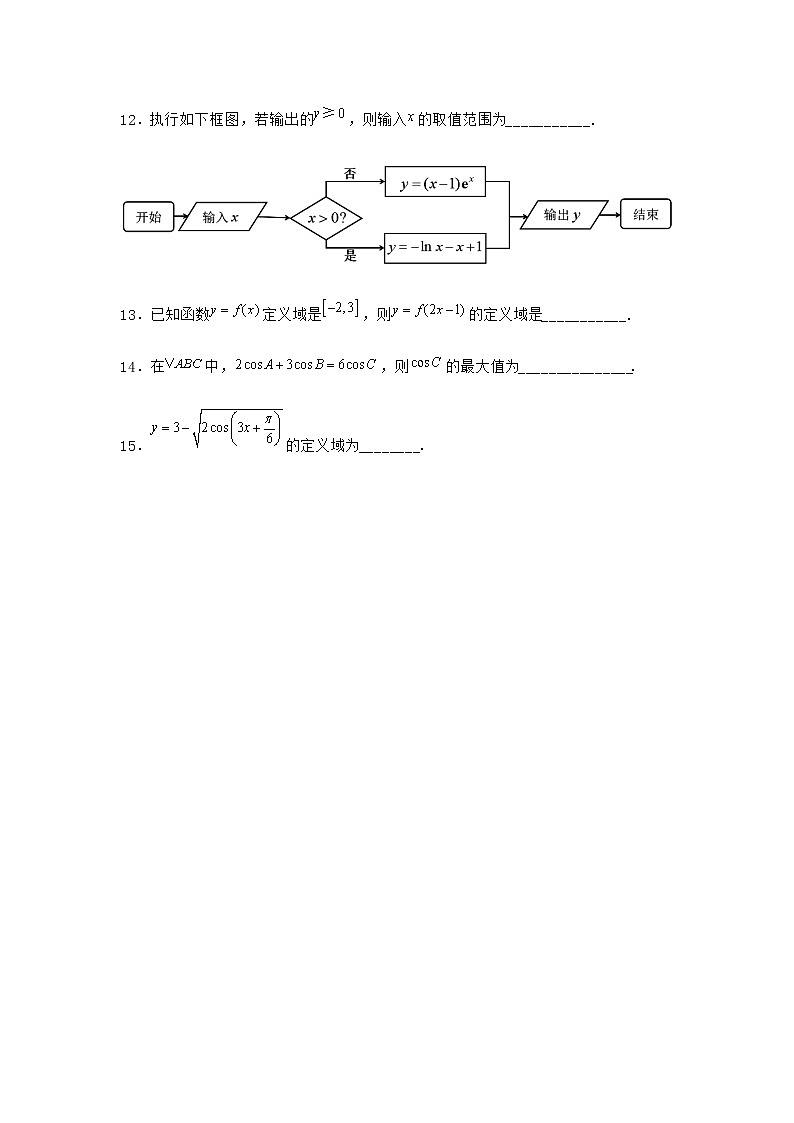
【精编】3 函数的单调性和最值-1课堂练习一．填空题1．设是定义在上的增函数，且，对于任意正数．满足等式，不等式的解集为______2．已知函数在区间上恒有，则实数的取值范围为______.3．已知函数的定义域为，且，则________．4．设函数若，则的取值范围是___________.5．已知函数的定义域为，则函数的定义域为_______6．已知函数，则__________.7．函数，若，则实数m的取值范围是_________．8．已知函数，则对任意的恒成立的充要条件是______．9．已知函数，则不等式的解集为____________ ．10．已知，，则的最大值为__________.11．已知函数在区间上的最大值是1，则实数a的取值范围是____.12．执行如下框图，若输出的，则输入的取值范围为___________.13．已知函数定义域是，则的定义域是___________.14．在中，，则的最大值为_______________．15．的定义域为________．
参考答案与试题解析1．【答案】.【解析】分析：根据题意，把不等式转化为，再结合函数的定义域和单调性，列出不等式组，即可求解.详解：由题意，函数满足对于任意正数．满足等式，因为，可得，且，由不等式，可转化为，又由是定义在上的增函数，可得，解得，即不等式的解集为.2．【答案】【解析】分析：先由函数在区间上有意义，可得，从而可得函数在区间上单调递减，所以由恒成立可得，进而可求出的取值范围详解：因为函数在区间上有意义，所以，同时，且，得，所以函数在区间上单调递减，因为函数在区间上恒有，所以，所以，得，因为，所以，故答案为：3．【答案】【解析】分析：将x换成，有，将该方程代入已知方程消去，可得答案．详解：在中，将x换成，则换成x，∴，将该方程代入已知方程消去，得．故答案为：．4．【答案】【解析】分析：根据题意,分类讨论求解即可.详解：解：当时，，解得；当时，，解得，综上，的取值范围是.故答案为：5．【答案】【解析】分析：根据具体函数和抽象函数的定义域求法，即可求解.详解：由条件可知，函数的定义域需满足，解得：，所以函数的定义域是.故答案为：6．【答案】10【解析】分析：先计算，再计算．详解：由题意，所以．故答案为：10.7．【答案】【解析】分析：结合函数的奇偶性和单调性进行解题即可.详解：解:因为为偶函数，且时，在上单调递减，在单调递增，若，则，解得.故答案为:．8．【答案】或.【解析】分析：根据题意，结合二次函数的性质，分和两种情况讨论，列出不等式组即可求解.详解：由题意，函数，因为对任意恒成立，即对任意的恒成立，当时，即时，若时，此时不等式对任意的恒成立；若时，此时不等式，显然不符合题意.当时，即时，要使得对任意恒成立，则满足，解得或，所以使得对任意恒成立的充要条件为或.故答案为：或.9．【答案】【解析】分析：由的单调性可得结果.详解：因为是上的增函数，所以.故答案为：.10．【答案】【解析】分析：先把原式平方，整理成的形式，再令进行换元，然后利用函数单调性求出最大值．详解：解：设，则，设，则，因为，所以，所以，当时，单调递减，所以当时，取得最大值为，所以，故答案为：.11．【答案】.【解析】分析：由已知可得，即，得到，再求解绝对值不等式，得到，先得出的范围，进而得到a的范围.详解：∵函数在区间上的最大值是1，∴，∴，∵，∴，∴.∴.故答案为：.12．【答案】【解析】分析：分两种情况解不等式，当时，；当时，，即可求解.详解：由题意可得：，当时，；因为时，且在上单调递增，所以可得，当时，，因为，，不成立，此时无解，综上所述：输入的取值范围为，故答案为：.13．【答案】【解析】分析：由题意可得出，进而可解得函数的定义域．详解：由题意可得出，解得：因此，函数的定义域为．故答案为：．14．【答案】【解析】详解：令，则，即．因为，所以，整理得，，化简得，于是，得，所以的最大值为．故答案为：.15．【答案】【解析】分析：由题意列不等式组，即可求出定义域.详解：要使函数有意义，只需，即，解得：，即函数的定义域为.故答案为：.