北师大版 (2019)必修 第一册3 函数的单调性和最值课时训练

【优编】3 函数的单调性和最值-4优选练习

一．填空题

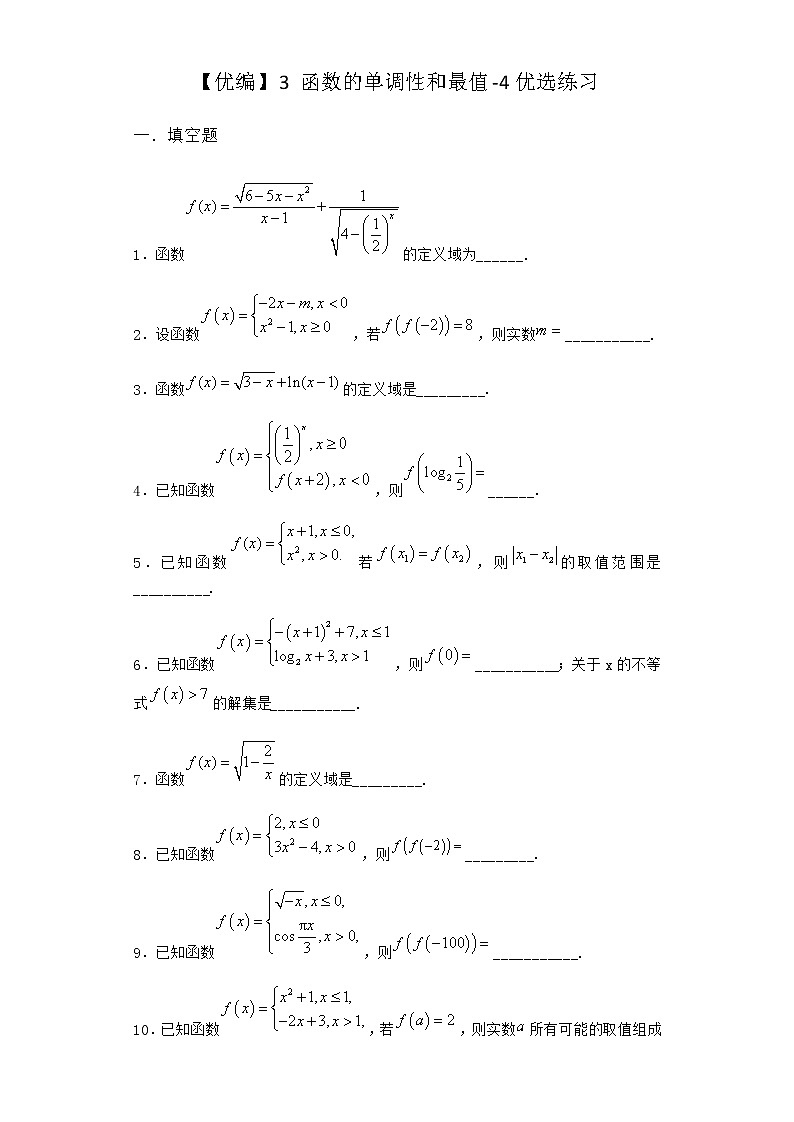
1．函数的定义域为______.

2．设函数，若，则实数___________.

3．函数的定义域是_________．

4．已知函数，则______．

5．已知函数若，则的取值范围是__________．

6．已知函数，则___________；关于x的不等式的解集是___________.

7．函数的定义域是_________.

8．已知函数，则_________．

9．已知函数，则___________.

10．已知函数，若，则实数所有可能的取值组成的集合为______．

11．存在函数，对于任意都成立的下列等式的序号是________．

①；②；③；④．

12．在上函数满足，且，其中，若，则_________.

13．函数的定义域为_____.

14．设函数，则___________.

15．已知函数，则______．

参考答案与试题解析

1．【答案】

【解析】分析：由被开方数大于等于0，分母不等于0列出不等式组，再求交集即可.

详解：函数的自变量满足：，

解得即

故答案为：.

2．【答案】1或16

【解析】分析：由题意得，分别讨论和，代入不同解析式，结合题意，即可求得答案.

详解：由题意得：，

若，则，即，解得，满足题意；

若，则，即，解得，满足题意，

综上，m的值为1或16.

故答案为：1或16

3．【答案】

【解析】分析：根据偶次根式被开方数大于等于零，和对数的真数大于零即可求出答案．

详解：解：由题意得，解得，

∴函数的定义域为，

故答案为：．

4．【答案】

【解析】分析：判断的范围，然后利用时，进行转化，将转化为，然后再利用分段函数的解析式求解即可．

详解：函数，

因为，且，

则

．

故答案为：．

5．【答案】

【解析】分析：设，且，结合图象有，从而得到求解.

详解：函数的图象如图所示：

设，且，

则，

所以，

，

，

令，则，

其对称轴为，

所以在上递增，在上递增，

所以，，

所以的取值范围是，

故答案为：

6．【答案】6     

【解析】分析：根据分段函数直接计算可得，然后分类讨论计算可得不等式的解集.

详解：由题可知：，所以

①，②

所以的解集是

故答案为：6，

7．【答案】

【解析】分析：根据函数有意义得，解不等式即可求解.

详解：解：由题意得：，

即，

即，

解得：或，

定义域是.

故答案为：.

8．【答案】8

【解析】分析：根据分段函数的概念，先计算的值，再根据取值重新代入求值即可.

详解：解：当时，，则.

故答案为：8.

9．【答案】

【解析】分析：首先求出的值，再将结果代入函数即可求得最终结果.

详解：由题意知，

则.

故答案为：.

10．【答案】{-1,1}

【解析】分析：这是个分段函数已知值求自变量的问题，根据分段函数在不同区间函数表达式不同分别求解即可，注意自变量的范围.

详解：当时，即，得，满足条件;

当时，即，得，不满足，故舍去;

所以a的取值集合为{-1,1}.

故答案为：{-1,1}

【点睛】

根据x1和x<1分别计算，要注意是否符合前提条件.

11．【答案】④

【解析】分析：根据函数定义逐项判断①②③，采用换元的方法求解④中的解析式并进行判断.

详解：①当时，；当时，，与函数定义矛盾，不符合；

②当时，；当时，，与函数定义矛盾，不符合；

③当时，；当时，，与函数定义矛盾，不符合；

④令，所以，令，所以，

所以，所以，符合，

故答案为：④.

【点睛】

关键点点睛：解答本题的关键在于对于函数定义的理解以及换元法求解函数解析式的运用，通过说明一个自变量的值对应两个不同的的值，判断出不符合函数定义；同时在使用换元法求解函数解析式时，新元取值范围的分析不能遗漏.

12．【答案】4.5

【解析】分析：由，可知函数的周期为2，所以，，再根据函数表达式将计算出来，根据求得.

详解：因为，所以函数的周期为2；又因为，，，所以，即.

故答案为：4.5.

【点睛】

若说明函数的周期为，若说明函数的周期为，若说明函数图像关于直线对称，若说明函数图像关于点对称.

13．【答案】

【解析】分析：利用对数和偶次根式有意义的条件限制列不等式，计算即得结果．

详解：依题意知，函数有意义，则需，解得，故定义域为．

故答案为：．

14．【答案】

【解析】分析：根据分段函数的解析式，计算即可.

详解：因为，

所以，

故答案为：1.

【点睛】

本题主要考查分段函数的函数值计算，属于简单题.

15．【答案】

【解析】分析：利用分段函数直接进行求值即可．

详解：∵函数，

∴，

∴

故答案为：.