浙江省杭州市余杭区绿城亲亲学校2022-2023学年九年级（上）月考数学试卷（12月份）(解析版)

这是一份浙江省杭州市余杭区绿城亲亲学校2022-2023学年九年级（上）月考数学试卷（12月份）(解析版)，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2022-2023学年浙江省杭州市余杭区绿城亲亲学校九年级（上）月考数学试卷（12月份）
一、选择题：本大题有10个小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知⊙O的半径是3，点P在圆外，则线段OP的长可能是（　　）
A．1 B．2 C．3 D．4
2．把一枚均匀的骰子抛掷一次，朝上一面的点数为3的概率是（　　）
A． B． C． D．
3．抛物线y＝（x﹣3）2+1的顶点坐标为（　　）
A．（3，﹣1） B．（3，1） C．（﹣3、﹣1） D．（﹣3，1）
4．已知点C是线段AB的黄金分割点（AC＞BC），若AB＝4，则AC的长为（　　）
A．（6﹣2） B．（2﹣2） C．（﹣1） D．（3﹣）
5．如图，已知AB∥CD∥EF，AD：DF＝2：3，BE＝15，那么BC的长为（　　）

A．5 B．6 C．7 D．8
6．如图，AB是半圆O的直径，点D是弧AC的中点，若∠BAC＝44°，则∠DAC等于（　　）

A．22° B．44° C．23° D．46°
7．已知（m﹣1，y1），（m，y2），（m+2，y3）是二次函数y＝﹣x2+2mx+n图象上的点，则有（　　）
A．y1＜y2＜y3 B．y3＜y2＜y1 C．y1＜y3＜y2 D．y3＜y1＜y2
8．下列有关圆的一些结论：①平分弧的直径垂直于弧所对的弦；②平分弦的直径垂直于弦；③在同圆或等圆中，相等的弦所对的圆周角相等；④同弧或等弧所对的弦相等，其中正确的有（　　）
A．①④ B．②③ C．①③ D．②④
9．如图，AB为⊙O的直径，且AB＝26，点C为⊙O上半圆的一点，CE⊥AB于点E，∠OCE的角平分线交⊙O于点D，弦AC＝10，那么△ACD的面积是（　　）

A．80 B．85 C．90 D．95
10．已知二次函数y＝x2+bx+c，当m≤x≤m+1时，此函数最大值与最小值的差（　　）
A．与m，b，c的值都有关
B．与m，b，c的值都无关
C．与m，b的值都有关，与c的值无关
D．与b，c的值都有关，与m的值无关
二、填空题：本大题有6个小题，每小题4分，共24分.
11．（4分）若2x＝3y，则的值是 　 　．
12．（4分）若四边形ABCD是圆内接四边形，它的内角∠B：∠D＝4：5，则∠B的度数是 　 　．
13．（4分）已知一个不透明的盒子里装有4个球，其中3个黑球，1个白球，这些球除颜色外其他均相同，现从中任意摸出两个球，恰好都是黑球的概率是 　 　．
14．（4分）在平面直角坐标系中，将抛物线y＝x2先向左平移1个单位，再向下平移2个单位，得到的抛物线表达式为 　 　．
15．（4分）如图，在矩形ABCD中，AB＝3，对角线AC，BD的交点为O，分别以A、D为圆心，AB的长为半径画弧，恰好经过点O，则图中阴影部分的面积为 　 　.（结果保留π）

16．（4分）对于二次函数y＝mx2﹣（4m+1）x+3m+3．有下列说法：
①若m＜0，当x≤2时，y随x的增大而增大；
②无论m为何值，该函数图象与，x轴必有交点；
③若m为整数，且该二次函数的图象与x轴的两个交点都为整数点，则m＝1；
④无论m为何值，该函数图象一定经过点（1，2）和（3，0）两点．
其中正确的是 　 　.（只需填写序号）
三、解答题：本大题有7个小题，共66分.解答应写出文字说明、证明过程或演算步骤.
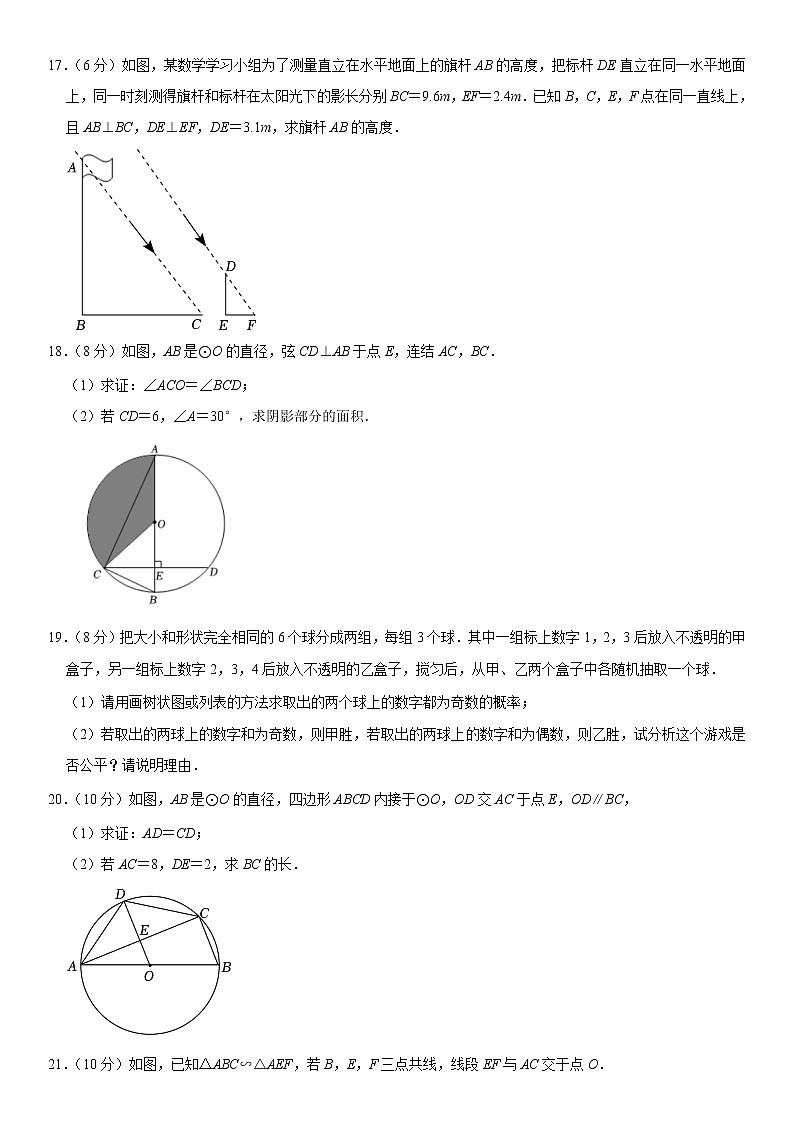
17．（6分）如图，某数学学习小组为了测量直立在水平地面上的旗杆AB的高度，把标杆DE直立在同一水平地面上，同一时刻测得旗杆和标杆在太阳光下的影长分别BC＝9.6m，EF＝2.4m．已知B，C，E，F点在同一直线上，且AB⊥BC，DE⊥EF，DE＝3.1m，求旗杆AB的高度．

18．（8分）如图，AB是⊙O的直径，弦CD⊥AB于点E，连结AC，BC．
（1）求证：∠ACO＝∠BCD；
（2）若CD＝6，∠A＝30°，求阴影部分的面积．

19．（8分）把大小和形状完全相同的6个球分成两组，每组3个球．其中一组标上数字1，2，3后放入不透明的甲盒子，另一组标上数字2，3，4后放入不透明的乙盒子，搅匀后，从甲、乙两个盒子中各随机抽取一个球．
（1）请用画树状图或列表的方法求取出的两个球上的数字都为奇数的概率；
（2）若取出的两球上的数字和为奇数，则甲胜，若取出的两球上的数字和为偶数，则乙胜，试分析这个游戏是否公平？请说明理由．
20．（10分）如图，AB是⊙O的直径，四边形ABCD内接于⊙O，OD交AC于点E，OD∥BC，
（1）求证：AD＝CD；
（2）若AC＝8，DE＝2，求BC的长．

21．（10分）如图，已知△ABC∽△AEF，若B，E，F三点共线，线段EF与AC交于点O．
（1）求证：△ABE∽△ACF；
（2）若AF＝5，BC＝10，△AOF的面积为8，求△BOC的面积．

22．（12分）在平面直角坐标系中，已知二次函数y＝﹣x2+2kx+k﹣1（k是常数）．
（1）当k＝﹣2时，求该二次函数图象与x轴的交点坐标；
（2）若该函数图象经过点（1，4），求该二次函数图象的顶点坐标；
（3）当0≤x≤1时，该函数有最大值4，求k的值．
23．（12分）如图1，是以点O为圆心，AB为直径的圆形纸片，点C在⊙O上，将该圆形纸片沿直径CF对折，点B落在⊙O上的点D处（不与点A重合），将纸片还原后，连接CB，CD，AD．设CD与直径AB交于点E．
（1）求证：AD∥OC；
（2）如图2，当CD⊥AB时，若OC＝2，求BC的长；
（3）如图3，当AD＝DE时，若BC＝2，求AD的长．



2022-2023学年浙江省杭州市余杭区绿城亲亲学校九年级（上）月考数学试卷（12月份）
参考答案与试题解析
一、选择题：本大题有10个小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知⊙O的半径是3，点P在圆外，则线段OP的长可能是（　　）
A．1 B．2 C．3 D．4
【分析】直接根据点与圆的位置关系即可得出结论．
【解答】解：∵⊙O的半径是3，点P在圆外，
∴OP的长＞3．
故选：D．
2．把一枚均匀的骰子抛掷一次，朝上一面的点数为3的概率是（　　）
A． B． C． D．
【分析】根据概率公式进行求解即可得出答案．
【解答】解：∵任意抛掷一次骰子共有6种等可能结果，其中朝上面的点数为3的只有1种，
∴朝上面的点数为3的概率是．
故选：A．
3．抛物线y＝（x﹣3）2+1的顶点坐标为（　　）
A．（3，﹣1） B．（3，1） C．（﹣3、﹣1） D．（﹣3，1）
【分析】根据二次函数顶点式解析式写出顶点坐标即可．
【解答】解：抛物线y＝（x﹣3）2+1的顶点坐标为（3，1）．
故选：B．
4．已知点C是线段AB的黄金分割点（AC＞BC），若AB＝4，则AC的长为（　　）
A．（6﹣2） B．（2﹣2） C．（﹣1） D．（3﹣）
【分析】根据黄金比值是计算即可．
【解答】解：∵点C是线段AB的黄金分割点，且AC＞BC，
∴AC＝AB＝2（﹣1），
故选：B．
5．如图，已知AB∥CD∥EF，AD：DF＝2：3，BE＝15，那么BC的长为（　　）

A．5 B．6 C．7 D．8
【分析】由AB∥CD∥EF，利用平行线分线段成比例，可求出BC的长．
【解答】解：∵AB∥CD∥EF，
∴＝，
即＝，
∴BC＝6．
故选：B．
6．如图，AB是半圆O的直径，点D是弧AC的中点，若∠BAC＝44°，则∠DAC等于（　　）

A．22° B．44° C．23° D．46°
【分析】根据直径所对的圆周角是直角可得∠ACB＝90°，从而利用直角三角形的两个锐角互余可得∠B＝46°，然后利用圆内接四边形对角互补可得∠D＝134°，再根据已知可得＝，进而可得AD＝DC，最后利用等腰三角形的性质，以及三角形内角和定理进行计算即可解答．
【解答】解：∵AB是半圆O的直径，
∴∠ACB＝90°，
∵∠BAC＝44°，
∴∠B＝90°﹣∠BAC＝46°，
∵四边形ABCD是半⊙O的内接四边形，
∴∠D＝180°﹣∠B＝134°，
∵点D是弧AC的中点，
∴＝，
∴AD＝DC，
∴∠DAC＝∠DCA＝（180°﹣∠D）＝23°，
故选：C．
7．已知（m﹣1，y1），（m，y2），（m+2，y3）是二次函数y＝﹣x2+2mx+n图象上的点，则有（　　）
A．y1＜y2＜y3 B．y3＜y2＜y1 C．y1＜y3＜y2 D．y3＜y1＜y2
【分析】求得抛物线的开口方向和对称轴，然后根据二次函数的性质即可得到结论．
【解答】解：∵y＝﹣x2+2mx+n，
∴抛物线开口向下，对称轴为直线x＝﹣＝m，
∵m﹣（m﹣1）＜（m+2）﹣m，
∴y3＜y1＜y2，
故选：D．
8．下列有关圆的一些结论：①平分弧的直径垂直于弧所对的弦；②平分弦的直径垂直于弦；③在同圆或等圆中，相等的弦所对的圆周角相等；④同弧或等弧所对的弦相等，其中正确的有（　　）
A．①④ B．②③ C．①③ D．②④
【分析】利用等弧的定义、圆周角定理、垂径定理及其推理分别判断后即可确定正确的选项．
【解答】解：①平分弧的直径垂直于弧所对的弦，故正确；
②平分弦（不是直径）的直径垂直于弦，故错误；
③在同圆或等圆中，相等的弦对应的圆周角相等或互补，故错误；
④同弧或等弧所对的弦相等；故正确；
正确的有2个，
故选：A．
9．如图，AB为⊙O的直径，且AB＝26，点C为⊙O上半圆的一点，CE⊥AB于点E，∠OCE的角平分线交⊙O于点D，弦AC＝10，那么△ACD的面积是（　　）

A．80 B．85 C．90 D．95
【分析】连接OD，过点A作AF⊥CD，垂足为F，根据直径所对的圆周角是直角可得∠ACB＝90°，从而可得∠ACE+∠ECB＝90°，再根据垂直定义可得∠CEB＝90°，从而可得∠CBE+∠ECB＝90°，进而可得∠ACE＝∠CBE，再利用等腰三角形的性质以及等量代换可得∠ACE＝∠OCB，然后利用角平分线的定义可得∠OCD＝∠ECD，从而利用等式的性质可得∠ACD＝45°，进而可得∠AOD＝2∠ACD＝90°，最后在Rt△ACF中，利用锐角三角函数的定义求出AF，CF的长，再在Rt△AOD中，利用等腰直角三角形的性质求出AD的长，从而在Rt△ADF中，利用勾股定理求出DF的长，进而求出CD的长，利用三角形的面积公式进行计算即可解答．
【解答】解：连接OD，过点A作AF⊥CD，垂足为F，

∵AB为⊙O的直径，
∴∠ACB＝90°，
∴∠ACE+∠ECB＝90°，
∵CE⊥AB，
∴∠CEB＝90°，
∴∠CBE+∠ECB＝90°，
∴∠ACE＝∠CBE，
∵OB＝OC，
∴∠CBE＝∠OCB，
∴∠ACE＝∠OCB，
∵CD平分∠OCE，
∴∠OCD＝∠ECD，
∴∠ACE+∠DCE＝∠OCB+∠OCD＝∠ACB＝45°，
∴∠ACD＝45°，
∴∠AOD＝2∠ACD＝90°，
在Rt△ACF中，AC＝10，
∴AF＝AC•sin45°＝10×＝5，
CF＝AC•cos45°＝10×＝5，
在Rt△AOD中，AO＝OD＝AB＝13，
∴AD＝AO＝13，
∴DF＝＝＝12，
∴CD＝CF+DF＝17，
∴△ACD的面积＝CD•AF
＝×17×5
＝85，
故选：B．
10．已知二次函数y＝x2+bx+c，当m≤x≤m+1时，此函数最大值与最小值的差（　　）
A．与m，b，c的值都有关
B．与m，b，c的值都无关
C．与m，b的值都有关，与c的值无关
D．与b，c的值都有关，与m的值无关
【分析】由抛物线解析式可得抛物线顶点坐标，从而可得函数最小值及对称轴，由﹣与m及m+1的关系可得函数最大值与最小值与m及b的值有关，进而求解．
【解答】解：∵y＝x2+bx+c＝（x+）2﹣+c，
∴抛物线开口向上，对称轴为直线x＝﹣，函数最小值为﹣+c，
将x＝m代入y＝x2+bx+c得y＝m2+bm+c，
将x＝m+1代入y＝x2+bx+c得y＝（m+1）2+b（m+1）+c，
当m+1＜﹣时，x＝m时y取最大值，x＝m+1时y取最小值，
当m＞﹣时，x＝m+1时y取最大值，x＝m时y取最小值，
∵m2+bm+c，（m+1）2+b（m+1）+c，﹣+c都含有c项，
∴函数最大值与最小值的差与m，b的值都有关，与c的值无关，
故选C．
二、填空题：本大题有6个小题，每小题4分，共24分.
11．（4分）若2x＝3y，则的值是 　　．
【分析】利用比例的性质，进行计算即可解答．
【解答】解：∵2x＝3y，
∴＝，
故答案为：．
12．（4分）若四边形ABCD是圆内接四边形，它的内角∠B：∠D＝4：5，则∠B的度数是 　80°　．
【分析】根据圆内接四边形的性质直接写出答案即可．
【解答】解：∵四边形ABCD是圆的内接四边形，
∴∠B+∠D＝180°，
∵∠B：∠D＝4：5，
∴∠B＝80°，
故答案为：80°．
13．（4分）已知一个不透明的盒子里装有4个球，其中3个黑球，1个白球，这些球除颜色外其他均相同，现从中任意摸出两个球，恰好都是黑球的概率是 　　．
【分析】画树状图，共有12种等可能的结果，其中恰好都是黑球的结果有6种，再由概率公式求解即可．
【解答】解：画树状图如下：

共有12种等可能的结果，其中恰好都是黑球的结果有6种，
∴恰好都是黑球的概率是＝，
故答案为：．
14．（4分）在平面直角坐标系中，将抛物线y＝x2先向左平移1个单位，再向下平移2个单位，得到的抛物线表达式为 　y＝﹣2（x+1）2﹣2　．
【分析】根据二次函数图象左加右减，上加下减的平移规律进行求解．
【解答】解：将抛物线y＝﹣2x2先向左平移1个单位，再向下平移2个单位，得到的抛物线的表达式是：y＝﹣2（x+1）2﹣2．
故答案是：y＝﹣2（x+1）2﹣2．
15．（4分）如图，在矩形ABCD中，AB＝3，对角线AC，BD的交点为O，分别以A、D为圆心，AB的长为半径画弧，恰好经过点O，则图中阴影部分的面积为 　﹣6π　.（结果保留π）

【分析】根据已知得△AOB，△COD都为边长为3的等边三角形，BC＝3，所以阴影部分的面积为三角形OBC的面积减去两个弓形的面积．
【解答】解：根据已知得△AOB，△COD都为边长为3的等边三角形，
∴BC＝3，
∵△AOB，△COD的面积为3×＝，扇形BAO和扇形CDO的面积为＝3π，
∴阴影部分的面积为3×﹣2×（3π﹣）＝﹣6π．
故答案为：﹣6π．
16．（4分）对于二次函数y＝mx2﹣（4m+1）x+3m+3．有下列说法：
①若m＜0，当x≤2时，y随x的增大而增大；
②无论m为何值，该函数图象与，x轴必有交点；
③若m为整数，且该二次函数的图象与x轴的两个交点都为整数点，则m＝1；
④无论m为何值，该函数图象一定经过点（1，2）和（3，0）两点．
其中正确的是 　②④　.（只需填写序号）
【分析】根据题目中的函数解析式和二次函数的性质，可以判断各个小题中的结论是否成立，从而可以解答本题．
【解答】解：∵二次函数y＝kx2﹣（4k+1）x+3k+3的对称轴是直线x＝﹣＝2+，
∴若m＜0，则2+＜2，该函数图象开口向下，
∴若m＜0，当x≤k时，y随x的增大而增大，故①错误；
∵y＝mx2﹣（4m+1）x+3m+3＝[mx﹣（m+1）]（x﹣3）＝[m（x﹣1）﹣1]（x﹣3），
∴对于任何满足条件的m，该二次函数的图象都经过点（1，2）和（3，0）两点，
∴对于任何满足条件的k，该二次函数中当x＝3时，y＝0，即该函数图象与x轴必有交点，故②，④正确；
∵y＝mx2﹣（4m+1）x+3m+3＝[mx﹣（m+1）]（x﹣3）＝[m（x﹣1）﹣1]（x﹣3），
∴当y＝0时，x1＝+1，x2＝3，
∴若m为整数，且该二次函数的图象与x轴的两个交点都为整数点，那么m＝±1，故③错误．
故答案为：②④．
三、解答题：本大题有7个小题，共66分.解答应写出文字说明、证明过程或演算步骤.
17．（6分）如图，某数学学习小组为了测量直立在水平地面上的旗杆AB的高度，把标杆DE直立在同一水平地面上，同一时刻测得旗杆和标杆在太阳光下的影长分别BC＝9.6m，EF＝2.4m．已知B，C，E，F点在同一直线上，且AB⊥BC，DE⊥EF，DE＝3.1m，求旗杆AB的高度．

【分析】根据平行投影得AC∥DF，可得∠ACB＝∠DFE，证明Rt△ABC∽△Rt△DEF，然后利用相似三角形的性质即可求解．
【解答】解：∵同一时刻测得旗杆和标杆在太阳光下的影长分别是BC＝9.6m，EF＝2.4m．
∴AC∥DF，
∴∠ACB＝∠DFE，
∵AB⊥BC，DE⊥EF，
∴∠ABC＝∠DEF＝90°，
∴Rt△ABC∽△Rt△DEF，
∴，即＝，
解得AB＝12.4，
∴旗杆的高度为12.4m．
故旗杆AB的高度为12.4m．
18．（8分）如图，AB是⊙O的直径，弦CD⊥AB于点E，连结AC，BC．
（1）求证：∠ACO＝∠BCD；
（2）若CD＝6，∠A＝30°，求阴影部分的面积．

【分析】（1）根据垂径定理得到＝，根据圆周角定理证明结论；
（2）根据等边三角形的判定定理得到△BOC为等边三角形，求出∠AOC，根据正弦的定义求出OC，利用扇形面积公式计算即可．
【解答】（1）证明：∵AB是⊙O的直径，弦CD⊥AB，
∴＝，
∴∠A＝∠BCD，
∵OA＝OC，
∴∠A＝∠ACO，
∴∠ACO＝∠BCD；
（2）解：∵∠A＝30°，
∴∠BOC＝60°，
∴∠AOC＝120°，
∵AB是⊙O的直径，弦CD⊥AB，
∴CE＝CD＝3，
在Rt△COE中，OC＝＝2，
∴扇形OAC（阴影部分）的面积＝＝4π，
答：阴影部分的面积为4π．
19．（8分）把大小和形状完全相同的6个球分成两组，每组3个球．其中一组标上数字1，2，3后放入不透明的甲盒子，另一组标上数字2，3，4后放入不透明的乙盒子，搅匀后，从甲、乙两个盒子中各随机抽取一个球．
（1）请用画树状图或列表的方法求取出的两个球上的数字都为奇数的概率；
（2）若取出的两球上的数字和为奇数，则甲胜，若取出的两球上的数字和为偶数，则乙胜，试分析这个游戏是否公平？请说明理由．
【分析】（1）列表得出所有等可能结果，从中找到符合条件的结果数，再根据概率公式求解即可；
（2）列表得出所有等可能结果，从中找到甲、乙获胜的结果数，再根据概率公式求解即可．
【解答】解：（1）列表如下：

1
2
3
2
（1，2）
（2，2）
（3，2）
3
（1，3）
（2，3）
（3，3）
4
（1，4）
（2，4）
（3，4）
由表知，共有9种等可能结果，其中取出的两个球上的数字都为奇数的有2种结果，
所以取出的两个球上的数字都为奇数的概率为；
（2）这个游戏不公平，理由如下：
列表如下：

1
2
3
2
3
4
5
3
4
5
6
4
5
6
57
由表知，共有9种等可能结果，其中两球上的数字和为奇数的有5种结果，和为偶数的有4种结果，
所以甲获胜的概率为，乙获胜的概率为，
∵≠，
∴这个游戏不公平．
20．（10分）如图，AB是⊙O的直径，四边形ABCD内接于⊙O，OD交AC于点E，OD∥BC，
（1）求证：AD＝CD；
（2）若AC＝8，DE＝2，求BC的长．

【分析】（1）根据直径所对的圆周角是直角可得∠ACB＝90°，再利用平行线的性质可得∠AEO＝∠ACB＝90°，然后利用垂径定理可得＝，从而可得AD＝CD，即可解答；
（2）利用垂径定理可得AE＝4，然后设⊙O的半径为r，则OE＝r﹣2，在Rt△AEO中，利用勾股定理列出关于r的方程，从而求出AB的长，最后在Rt△ACB中，利用勾股定理进行计算即可解答．
【解答】（1）证明：∵AB是⊙O的直径，
∴∠ACB＝90°，
∵OD∥BC，
∴∠AEO＝∠ACB＝90°，
∴＝，
∴AD＝CD；
（2）解：∵OD⊥AC，AC＝8，
∴AE＝AC＝4，
设⊙O的半径为r，
∵DE＝2，
∴OE＝OD﹣DE＝r﹣2，
在Rt△AEO中，AE2+OE2＝AO2，
∴16+（r﹣2）2＝r2，
解得：r＝5，
∴AB＝2r＝10，
在Rt△ACB中，BC＝＝＝6，
∴BC的长为6．
21．（10分）如图，已知△ABC∽△AEF，若B，E，F三点共线，线段EF与AC交于点O．
（1）求证：△ABE∽△ACF；
（2）若AF＝5，BC＝10，△AOF的面积为8，求△BOC的面积．

【分析】（1）由△ABC∽△AEF，可得∠BAC＝∠EAF，AB：AE＝AC：AF，可得∠BAE＝∠CAF，所以AB：AC＝AE：AF，由两边对应成比例且夹角相等的三角形相似可得结论；
（2）由（1）知，△ABE∽△ACF，所以∠ABE＝∠ACF，易证△AOB∽△FOC，进而可得△AOF∽△BOC，所以S△BOC：S△AOF＝（）2＝4，由此可得结论．
【解答】（1）证明：∵△ABC∽△AEF，
∴∠BAC＝∠EAF，AB：AE＝AC：AF，
∴∠BAC﹣∠EAC＝∠EAF﹣∠EAC，即∠BAE＝∠CAF，
∴AB：AC＝AE：AF，
∴△ABE∽△ACF；
（2）解：由（1）知，△ABE∽△ACF，
∴∠ABE＝∠ACF，
∵∠AOB＝∠COF，
∴△AOB∽△FOC，
∴AO：OF＝OB：OC，
∵∠AOF＝∠BOC，
∴△AOF∽△BOC，
∴S△BOC：S△AOF＝（）2＝4，
∵S△AOF＝8，
∴S△BOC＝32．
22．（12分）在平面直角坐标系中，已知二次函数y＝﹣x2+2kx+k﹣1（k是常数）．
（1）当k＝﹣2时，求该二次函数图象与x轴的交点坐标；
（2）若该函数图象经过点（1，4），求该二次函数图象的顶点坐标；
（3）当0≤x≤1时，该函数有最大值4，求k的值．
【分析】（1）当k＝﹣2时求出二次函数解析式，再令y＝0，解方程即可；
（2）把点（1，4）代入函数解析式，求出k即可；
（3）先求出抛物线对称轴直线为x＝k，再分k≥1，k≤0和0＜k＜1三种情况由函数的性质进行解答即可．
【解答】解：（1）当k＝﹣2时，二次函数解析式为y＝﹣x2﹣4x﹣3，
令y＝0，则﹣x2﹣4x﹣3＝0，
解得x1＝﹣1，x2＝﹣3，
∴当k＝﹣2时，求该二次函数图象与x轴的交点坐标为（﹣1，0），（﹣3，0）；
（2）∵二次函数y＝﹣x2+2kx+k﹣1的图象经过点（1，4），
∴﹣1+2k+k﹣1＝4，
解得k＝2，
∴y＝﹣x2+4x+1＝﹣（x﹣2）2+5，
∴该二次函数图象的顶点坐标为（2，5）；
（3）二次函数y＝﹣x2+2kx+k﹣1的对称轴为直线x＝﹣＝k，
①k≥1时，
当0≤x≤1时，y随x的增大而增大，
∴当x＝1时，y有最大值，即﹣1+2k+k﹣1＝4，
解得k＝2；
②k≤0时，
当0≤x≤1时，y随x的增大而减小，
∴当x＝0时，y有最大值，即k﹣1＝4，
解得k＝5；
③0＜k＜1时，
当0≤x≤1时，x＝k时，y最大，
∴﹣k2+2k2+k﹣1＝4，
解得k＝（不合题意），
∴k的值为2或5．
23．（12分）如图1，是以点O为圆心，AB为直径的圆形纸片，点C在⊙O上，将该圆形纸片沿直径CF对折，点B落在⊙O上的点D处（不与点A重合），将纸片还原后，连接CB，CD，AD．设CD与直径AB交于点E．
（1）求证：AD∥OC；
（2）如图2，当CD⊥AB时，若OC＝2，求BC的长；
（3）如图3，当AD＝DE时，若BC＝2，求AD的长．


【分析】（1）由折叠可得∠ECO＝∠BCO，由OB＝OC，可得∠OCB＝∠B，所以∠ECO＝∠B，根据同弧所对圆周角相等可得∠ADC＝∠ABC，等量代换可得∠ADC＝∠ECO，根据内错角相等，两直线平行即可得AD∥OC；
（2）结合（1）方法证明∠ECO＝∠OCB＝∠B＝30°，根据含30度角的直角三角形性质和OC＝OB＝2，即可解决问题；
（3）由等腰三角形的性质得出∠DAE＝∠DEA，证出∠BEC＝∠BCE，由折叠的性质得出∠ECO＝∠BCO，证明△CEO∽△BEC，由相似三角形的性质得出＝，设EO＝x，EC＝OC＝OB＝a，得出a2＝x（x+a），求出OE＝＝a，证明△BCE∽△DAE，由相似三角形的性质得出＝，则可得出答案．
【解答】（1）证明：由折叠可知：∠ECO＝∠BCO，
∵OB＝OC，
∴∠OCB＝∠B，
∵∠ECO＝∠B，
∵∠ADC＝∠ABC，
∴∠ADC＝∠ECO，
∴AD∥OC；
（2）由折叠可知：∠ECO＝∠BCO，
∵OB＝OC，
∴∠OCB＝∠B，
∴∠ECO＝∠OCB＝∠B，
∵CD⊥AB，
∴∠ECO+∠OCB+∠B＝90°，
∴∠ECO＝∠OCB＝∠B＝30°，
∵OC＝OB＝2，
∴OE＝1，
∴CE＝，
∴BC＝2CE＝2；
（3）解：∵AD＝DE，
∴∠DAE＝∠DEA，
∵∠DEA＝∠BEC，∠DAE＝∠BCE，
∴∠BEC＝∠BCE，
∵将该圆形纸片沿直线CF对折，
∴∠ECO＝∠BCO，
又∵OB＝OC，
∴∠OCB＝∠B，
∵∠ECO＝∠B，∠CEO＝∠CEB，
∴△CEO∽△BEC，
∴＝，
∴CE2＝EO•BE，
设EO＝x，EC＝OC＝OB＝a，
∴a2＝x（x+a），
解得，x＝a（负值舍去），
∴OE＝a，
∴AE＝OA﹣OE＝a﹣a＝a，
∵∠AED＝∠BEC，∠DAE＝∠BCE，
∴△BCE∽△DAE，
∴＝，
∵BC＝2，
＝，
∴AD＝3﹣．