广东省佛山市高明区高明实验中学2023届九年级上学期期中测试数学试卷(含答案)

这是一份广东省佛山市高明区高明实验中学2023届九年级上学期期中测试数学试卷(含答案)，共14页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
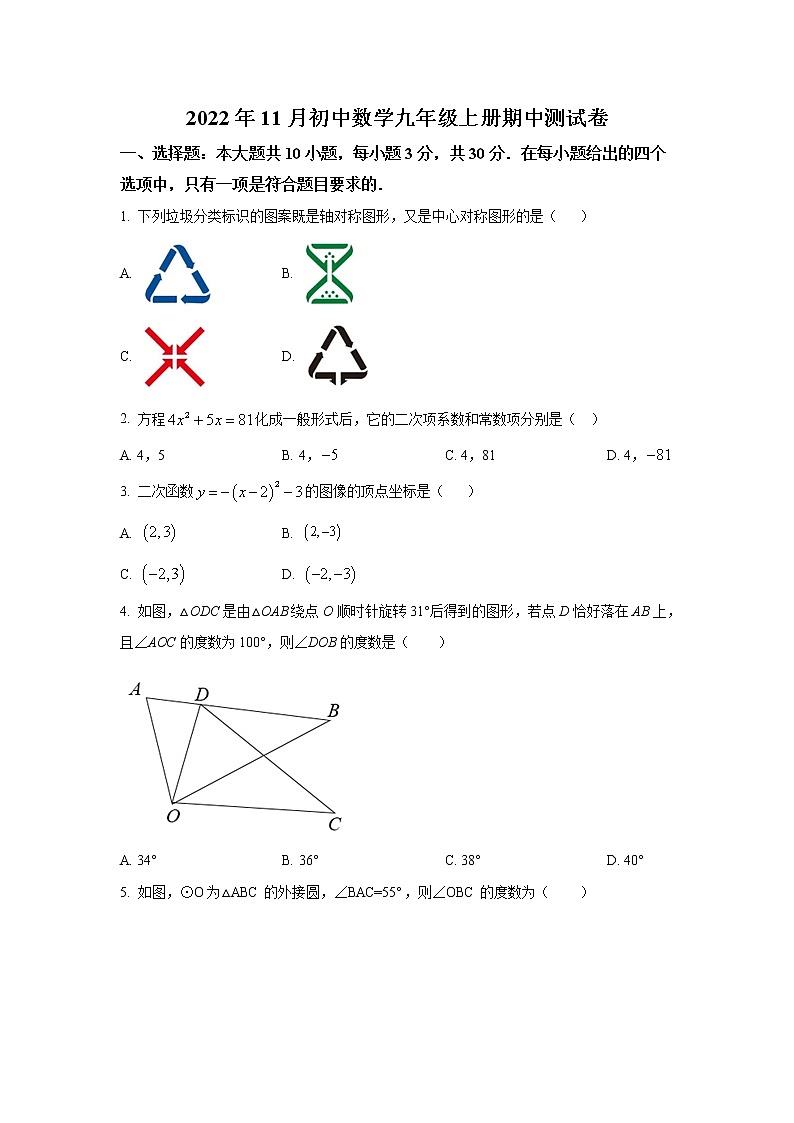
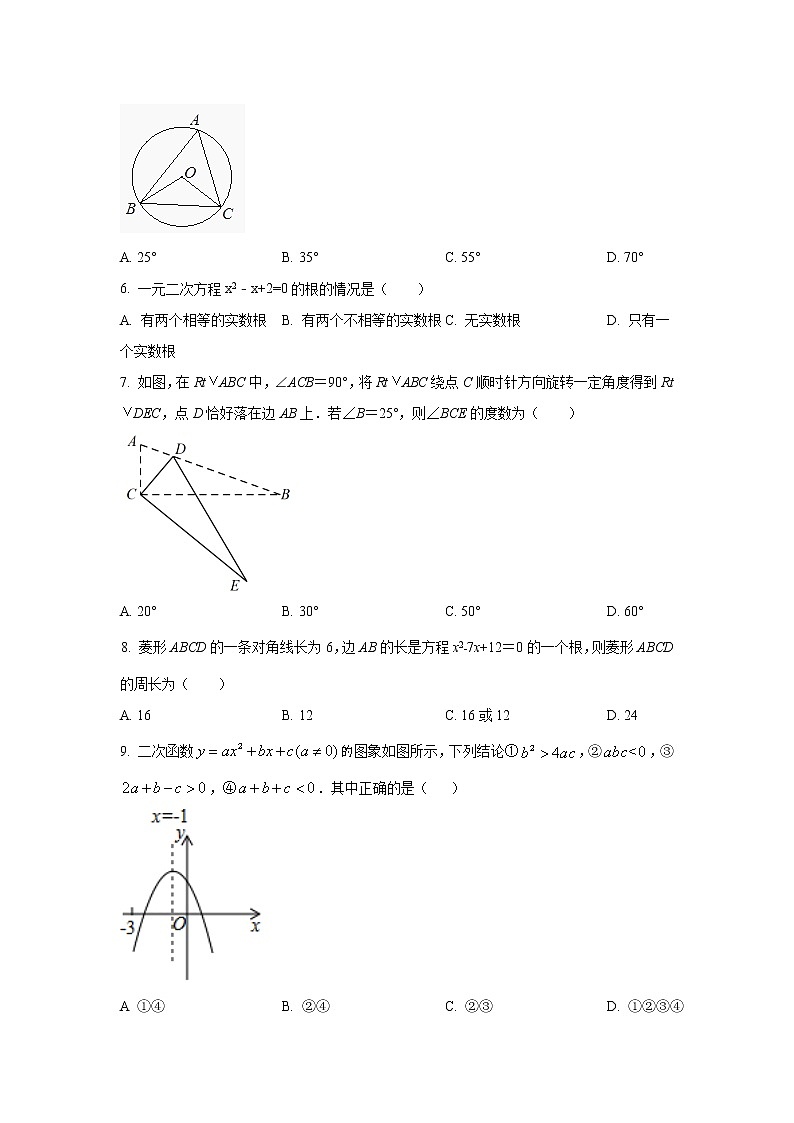
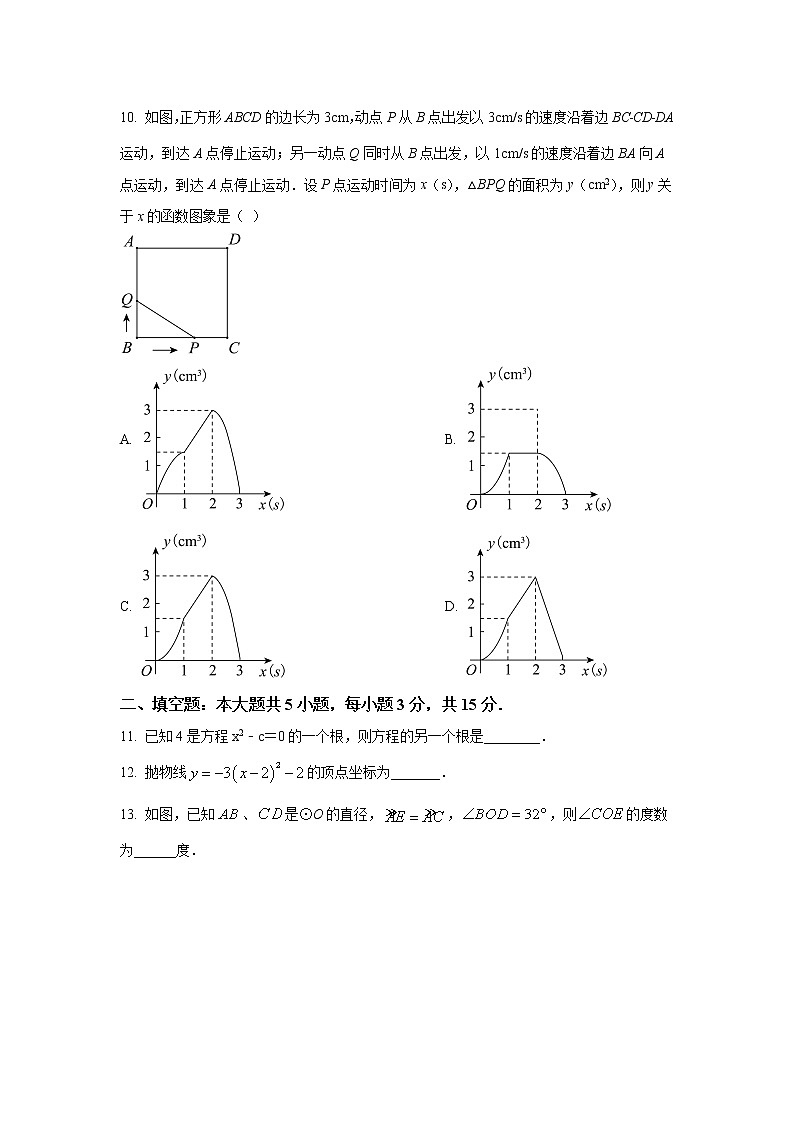
2022年11月初中数学九年级上册期中测试卷 一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 下列垃圾分类标识的图案既是轴对称图形，又是中心对称图形的是（    ）A.  B.  C.  D. 2. 方程化成一般形式后，它的二次项系数和常数项分别是（  ）A. 4，5 B. 4， C. 4，81 D. 4，3. 二次函数的图像的顶点坐标是（    ）A.  B.  C.  D. 4. 如图，△ODC是由△OAB绕点O顺时针旋转31°后得到的图形，若点D恰好落在AB上，且∠AOC的度数为100°，则∠DOB的度数是（　　）A. 34° B. 36° C. 38° D. 40°5. 如图，⊙O为△ABC的外接圆，∠BAC=55°，则∠OBC 的度数为（        ）A. 25° B. 35° C. 55° D. 70°6. 一元二次方程x2﹣x+2=0的根的情况是（　　）A. 有两个相等的实数根 B. 有两个不相等的实数根 C. 无实数根 D. 只有一个实数根7. 如图，在RtABC中，∠ACB＝90°，将RtABC绕点C顺时针方向旋转一定角度得到RtDEC，点D恰好落在边AB上．若∠B＝25°，则∠BCE的度数为（　　）A. 20° B. 30° C. 50° D. 60°8. 菱形ABCD的一条对角线长为6，边AB的长是方程x2﹣7x+12＝0的一个根，则菱形ABCD的周长为（　　）A. 16 B. 12 C. 16或12 D. 249. 二次函数图象如图所示，下列结论①，②，③，④．其中正确的是（    ）A ①④ B. ②④ C. ②③ D. ①②③④10. 如图，正方形ABCD的边长为3cm，动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动，到达A点停止运动；另一动点Q同时从B点出发，以1cm/s的速度沿着边BA向A点运动，到达A点停止运动．设P点运动时间为x（s），△BPQ的面积为y（cm2），则y关于x的函数图象是（ ）A.  B.  C.  D. 二、填空题：本大题共5小题，每小题3分，共15分．11. 已知4是方程x2﹣c＝0的一个根，则方程的另一个根是________．12. 抛物线的顶点坐标为_______．13. 如图，已知、是⊙O的直径，，，则的度数为______度．14. 二次函数，当时，的最大值和最小值的和是_______．15. 如图，圆心都在轴正半轴上的半圆，半圆，…，半圆与直线相切，设半圆，半圆，…，半圆的半径分别是，，…，，则当直线与轴所成锐角为，且时，______．三、解答题（一）：本大题共3小题，每小题8分，共24分．16. 解方程：．17. 已知抛物线y＝ax2+bx+c经过点A（1，0），B（﹣1，0），C（0，﹣2）．求此抛物线函数解析式和顶点坐标．18. 随着国内新能源汽车的普及，为了适应社会的需求，全国各地都在加快公共充电桩的建设，广东省2019年公共充电桩的数量约为4万个，2021年公共充电桩的数量多达11.56万个，位居全国首位．（1）求广东省2019年至2021年公共充电桩数量的年平均增长率；（2）按照这样增长速度，预计广东省2022年公共充电桩数量能否超过20万个？为什么？四、解答题（二）：本大题共3小题，每小题9分，共27分．19. 已知△ABC的顶点A、B、C在格点上，按下列要求在网格中画图．（1）△ABC绕点C顺时针旋转90°得到△A1B1C；（2）画△A1B1C关于点O的中心对称图形△A2B2C2．20. 如图，D△ABC内一点，AB＝AC，∠BAC＝50°，将AD绕着点A顺时针旋转50°能与线段AE重合．（1）求证：EB＝DC； （2）若∠ADC＝115°，求∠BED的度数．21. 已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C．（1）如图①，若∠P=35°，求∠ABP的度数；（2）如图②，若D为AP的中点，求证：直线CD是⊙O的切线．五、解答题（三）：本大题共2小题，每小题12分，共24分．22. 某服装店在服装销售中发现：进货价每件60元，销售价每件100元的某服装每天可售出20件，为了迎接新春佳节，服装店决定采取适当的促销措施，扩大销售量，增加盈利．经调查发现：如果每件服装降价1元，那么每天就可多售出2件．（1）如果服装店想每天销售这种服装盈利1050元，同时又要使顾客得到更多的实惠，那么每件服装应降价多少元？（2）每件服装降价多少元时，服装店每天可获得最大利润？最大利润是多少元？23. 如图，二次函数y＝ax2+bx﹣3的图象经过点(2，﹣3)和(1，﹣)，与x轴从左至右分别交于点A，B，点M为抛物线的顶点．（1）求二次函数的解析式．（2）在抛物线的对称轴上是否存在这样的点P，使得PAC的周长最小？若存在，请求出点P的坐标，若不存在，请说明理由．（3）连接BM，若点Q为线段OB上的一动点（Q不与点B、点O重合），过点Q作x轴的垂线交线段BM于点N，当点Q以1个单位/s的速度从点B向点O运动时，设运动时间为t，四边形OCNQ的面积为S，求S与t之间的函数关系及自变量t的取值范围，并求出S的最值．（4）若点R在抛物线上，且以点R、C、B为顶点的三角形是直角三角形，请直接写出所有符合条件的点R的坐标（不需要计算过程）．
  
答案 1-10 CDBCB  CCAAC  11. -412. 13. 14. 15. 3201716. 解：，，则或，解得，．17. 把点A（1，0）、B（-1，0）、C（0，-2）的坐标,分别代入得：，解得：， ∴二次函数的解析式为． ∴抛物线顶点坐标为（0，-2）．18. 解：（1）设广东省2019年至2021年公共充电桩数量的年平均增长率为解得：，（不合题意，舍去）答：年平均增长率为．（2）该省2022年公共充电桩数量答：预计广东省2022年公共充电桩数量不能超过20万个．19.（1）解：△ABC绕点C顺时针旋转90°得到△A1B1C如图所示；（2）解：△A1B1C关于点O的中心对称图形△A2B2C2如图所示；20. 证明（1）∵将AD绕着点A顺时针旋转50°能与线段AE重合，∴AD=AE，∠DAE=∠BAC＝50°，∴∠DAE-∠BAD=∠BAC-∠BAD，即∠BAE=∠CAD，∵AB=AC，∴△BAE≌△CAD，∴EB=DC；（2）∵△BAE≌△CAD，∴∠BEA=∠ADC=115°，∵∠DAE=50°，AD=AE，∴ ，∴∠BED=∠BEA-∠AED=115°-65°=50°．21. 解：（1）如图①中，连接OC．∵PA是⊙O的切线，∴PA⊥AB，∴∠PAB＝90°，∵∠P＝35°，∴∠B＝55°，∵OB＝OC，∴∠B＝∠OCB＝55°，∴∠BOC＝180°﹣55°﹣55°＝70°．（2）如图②中，连接OC，OD，AC．∵AB是直径，∴∠ACB＝∠ACP＝90°，∵AD＝DP，∴DC＝DA＝DB，∵OA＝OC，OD＝OD，∴△ODC≌△ODA（SSS），∴∠OCD＝∠OAD＝90°，∴OC⊥CD，∴DC是⊙O的切线．22. 解：（1）设每件服装降价x元,根据题意,得(100−60−x)(20+2x)=1050，  解得：  ∵要使顾客得到较多的实惠，∴ x=25，答：服装店应该降价元．（2）设每件服装降价a元，可获利W元，根据题意，得 化简得：∴ 答：每件服装降价15元服装店可获得最大利润，最大利润是1250元23. 解：（1）将代入中，得：解得：∴二次函数的解析式为：（2）存在点P使得的周长最小,此时，理由如下：∵点A、点B是抛物线与x轴的交点∴当时，即：解得：∵A在B的左边∴∵点C是抛物线与y轴的交点∴当时，∴又∵∴抛物线的对称轴为：过点C作关于对称轴的对称点,连接交对称轴于点P，此时的周长最小，如图1：∵点C与点关于对称轴对称∴设直线的解析式为，将代入得：解得：∴直线的解析式为：∵点P在上∴ ∴ ∴ （3）如图2：∵点M是抛物线的顶点，且∴设直线BM的解析式为：，将，代入得：，解得：∴直线BM的解析式为：∵有题意知：，且轴∴∴∴又∵∴∴∵点Q为线段OB上的一动点（Q不与点B、点O重合）∴∴S与t之间函数关系为：∵∴S有最大值又∵∴当时，S取得最大值（4）据题意，作图如下：设点在中，当时，在中，由勾股定理知：即：化简得：解得：（舍），∴当时，化简得：解得：（舍），∴综上所述，满足题意的R点有两个，分别是和