

江苏省泰州市姜堰区2023届九年级上学期期中学情调查数学试卷(含答案)
展开2022年秋学期期中学情调查
九年级数学试题
(考试时间:120分钟总分:150分)
请注意:1.所有试题的答案均填写在答题卡上,答案写在试卷上无效.
2.作图必须用2B铅笔,并请加黑加粗.
第一部分 选择题
一、选择题(本大题共6小题,每小题3分,共18分.在每小题所给出的四个选项中,只有一项是正确的,请把正确选项前的字母代号填涂在答题卡相应位置上)
1. 一元二次方程的根是( )
A. B.
C. , D. ,
2. 抛掷一枚硬币,若抛掷3次都是正面朝上,则抛掷第4次正面朝上的概率为( )
A. 小于 B. 等于 C. 大于 D. 无法确定
3. 小明不慎把家里的圆形镜子打碎了,其中四块多边形碎片如图所示,四块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A. ① B. ② C. ③ D. ④
4. 如图,在矩形中,cm,cm,点从点出发沿以cm/s的速度向点运动,当时,点运动的时间为( )
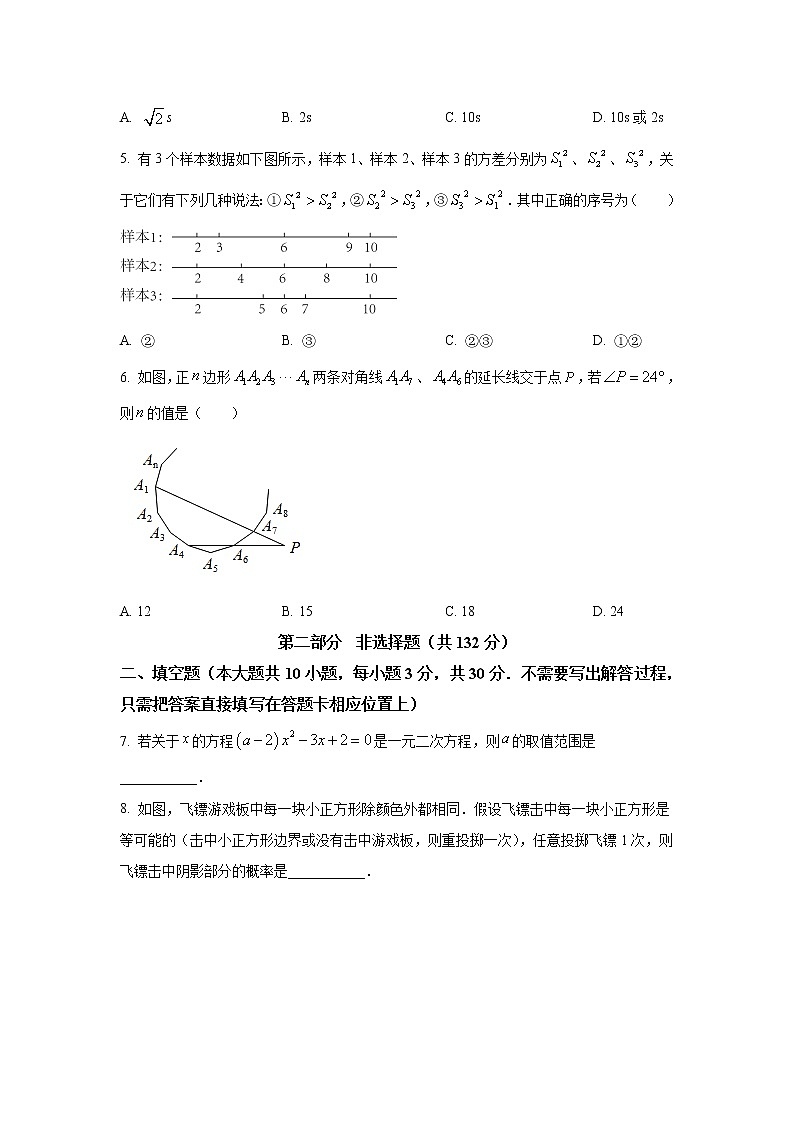
A. s B. 2s C. 10s D. 10s或2s
5. 有3个样本数据如下图所示,样本1、样本2、样本3的方差分别为、、,关于它们有下列几种说法:①,②,③.其中正确的序号为( )
A. ② B. ③ C. ②③ D. ①②
6. 如图,正边形两条对角线、的延长线交于点,若,则的值是( )
A. 12 B. 15 C. 18 D. 24
第二部分 非选择题(共132分)
二、填空题(本大题共10小题,每小题3分,共30分.不需要写出解答过程,只需把答案直接填写在答题卡相应位置上)
7. 若关于的方程是一元二次方程,则的取值范围是___________.
8. 如图,飞镖游戏板中每一块小正方形除颜色外都相同.假设飞镖击中每一块小正方形是等可能的(击中小正方形边界或没有击中游戏板,则重投掷一次),任意投掷飞镖1次,则飞镖击中阴影部分的概率是___________.
9. 某校艺术节的歌唱比赛最终得分由歌唱水平、舞台表现、专业知识三部分组成.小红这三项得分依次为90分、80分和90分,若把歌唱水平、舞台表现、专业知识的成绩按计算总分,则小红在这次比赛的总分为___________分.
10. 已知圆锥的母线长为4cm,底面圆的半径为3cm,则此圆锥的侧面积是_____cm2.
11. 观察表格,一元二次方程最精确的一个近似解___________(精确到).
x | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 |
12. 如图,已知,若将、向内折叠使得点A,B落在圆弧上的同一点C处,折痕为、,则___________°.
13. 为防控疫情,我们应该做到有“礼”有“距”,于是用“碰肘礼”代替“握手”的问候方式逐渐流行.某次会议上,每两个参会者都相互行了一次“碰肘礼”,经统计共碰肘28次,若设有人参加这次会议,则可列方程为___________.
14. 如图,在中,,,,点M,N分别是的内心和外心,则___________.
15. 若关于的一元二次方程有两个整数根,则整数的值是___________.
16. 如图,半圆的直径,弦,弦在半圆上滑动,点从点开始滑动,到点与点重合时停止滑动,若是的中点,则在整个滑动过程中线段扫过的面积为___________.
三、解答题(本大题共10小题,共102分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤)
17. 解方程:
(1);
(2).
18. 已知关于的一元二次方程.
(1)求证:无论取何值,方程总有两个实数根;
(2)若方程有一根为,求的值.
19. 2022年10月1日,中国女篮在世界杯比赛中表现不俗,获得本届女篮世界杯亚军,追平了世界杯历史最好战绩.她们的拼劲儿以及永不服输的女篮精神,值得我们学习.下䘚是小组赛的部分统计数据.
2022年女篮世界杯小组赛部分统计数据
国家 | 场均得分(分) | 场均篮板(个) | 场均助攻(次) | 场均失误(次) | 场均投篮命中率(%) | 场均罚球命中率(%) |
美国 | 107.2 | 46.6 | 28.4 | 10.6 | 55.1 | 80.6 |
中国 | 888 | 46.6 | 28.2 | 12.0 | 51.3 | 75.9 |
澳大利亚 | 78.0 | 45.8 | 214 | 14.2 | 41.3 | 76.9 |
比利时 | 72.8 | 39.6 | 22.8 | 15.0 | 43.4 | 74.3 |
加拿大 | 71.2 | 44.2 | 14.4 | 13.6 | 39.8 | 74.6 |
韩国 | 69.2 | 29.0 | 17.0 | 132 | 38.9 | 78.1 |
(1)上表中六国的“场均得分”的平均数为___________分;
(2)“场均篮板”这组数据的中位数是___________个,众数是___________个;
(3)请结合表中数据,从两个不同的角度简要评价中国女篮在本届世界杯中的表现.
20. 如图,转盘中3个扇形面积都相等.任意转动转盘,当指针落在两个扇形的交线上时,则重转一次.
(1)任意转动转盘1次,指针落在“勤洗手”区域的概率为___________;
(2)任意转动转盘2次,请用树状图或列表法求指针2次都落在“戴口罩”区域的概率.(注:指针落在“勤洗手”区域记为事件、落在“戴口罩”区域记为事件D.)
21. 如图,是的直径,点A、E在上,且在直径的两侧,点在直径上,的延长线交于点,、的延长线交于点,给出下列信息:①;②;③.请从上述三条信息中选择两条作为补充条件,余下的一条作为结论组成一个真命题,并说明理由.你选择的补充条件是___________,结论是___________(填写序号).证明:___________
22. 乌克兰危机发生之后,外交战线按照党中央的部署紧急行动,在战火纷飞中已将5200多名同胞安全从乌克兰撤离.电影《万里归途》正是“外交为民”的真实写照.下表是该影片票房的部分数据.(注:票房是指截止发布日期的所有售票累计收入)
影片《万里归途》的部分统计数据
发布日期 | 10月8日 | 10月10日 | 10月12日 |
发布次数 | 第1次 | 第2次 | 第3次 |
票房 | 10亿元 | 12.1亿元 |
(1)平均每次累计票房增长的百分率是多少?
(2)在(1)的条件下,若票价每张40元,求10月11日与12日两天共卖出多少张电影票.
23. 如图,是的内接三角形,直径,,过点的切线交的延长线于点.
(1)求的长;
(2)求图中阴影部分面积.
24. 规定:若(,m、n、p为有理数,为无理数)是一元二次方程(,a、b、c为有理数)根,则也是该方程的根,称是该方程的一对“共轭无理根”.
(1)写出一元二次方程的一对“共轭无理根”___________;
(2)若是关于的一元二次方程的一个根,求有理数b、c的值___________;
(3)关于的一元二次方程(,a、b为有理数)的一对“共轭无理根”是.若(m、n为有理数),求代数式的值.
25. 早在公元前古希腊数学家欧几里得就发现了垂径定理,即垂直于弦的直径平分弦.阿基米德从中看出了玄机并提出:如果条件中的弦变成折线段,仍然有类似的结论.
某数学兴趣小组对此进行了探究,如图1,和是的两条弦(即折线段是圆的一条折弦),,是的中点,过点作,垂足为,小明通过度量、、的长度,发现点平分折弦,即.小丽和小军改变折弦的位置发现仍然成立,于是三位同学都尝试进行了证明:
小军采用了“截长法”(如图2),在上㵶取,使得,……
小丽则采用了“补短法”(如图3),延长至,使,……
小明采用了“平行线法”(如图4),过点作,交圆于点,过点作,……
(1)请你任选一位同学的方法,并完成证明;
(2)如图5,在网格图中,每个小正方形边长均为1,内接于(A、B、C均是格点),点A、D关于对称,连接并延长交于点,连接.
①请用无刻度的直尺作直线,使得直线平分的周长;
②求的周长.
26. 如图1,在平面内,过外一点画它的两条切线,切点分別为M、N,若,则称点为的“限角点”.
(1)在平面直角坐标系中,当半径为1时,在①,②,③,④中,的“限角点”是___________;(填写序号)
(2)如图2,的半径为,圆心为,直线:交坐标轴于点B、C,若直线上有且只有一个的“限角点”,求的值;
(3)如图3,、、、的半径为,圆心从原点出发,以个单位的速度沿直线:向上运动,若三边上存在的“限角点”,请直接写出运动的时间的取值范围.
答案
1-6 CBBBD B
7.
8.
9. 87
10. 12π
11.
12. 145
13.
14.
15.
16.
17.(1)解:。
移项得:,
因式分解得:,
即,
∴或,
∴;
(2),
因式分解得:,
∴或,
∴.
18.(1)解:由一元二次方程的根的判别式,
取任意实数时,,即,
无论取何值,方程总有两个实数根,
故命题得证.
(2)把代入方程,得:,
解得,
故答案为:.
19. (1)81.2
(2)45,46.6
(3)从场均得分和场均篮板来看,中国女篮分别为第二名和第一名,说明中国女篮在本届世界杯中的表现非常优秀.
20. (1)
(2)解:列表如下:
| Q | D | D |
Q | |||
D | |||
D |
由表知,共有9种等可能结果,其中指针2次都落在“戴口罩”区域的有4种结果,
所以指针2次都落在“戴口罩”区域的概率为.
21.解:选择的补充条件是①②,结论③.
证明如下:
∵为直径,,
∴,,
∴,
∵为直径,,
∴,,
∴,
∵,
∴,
∴,
∵,,
∴,
∴.
故答案为:①②,③(答案不唯一).
22.(1)解:设平均每次累计票房增长的百分率是x,
依题意得:,
解得:,(不符合题意,舍去),
.
答:平均每次累计票房增长的百分率是.
(2)解:
(张).
答:10月11日与12日两天共卖出2750000张电影票.
23.(1)解:∵是的直径,
∴,
∴,
∵,
∴,,
∴ ,
∴ ,
∵ 是的切线,
∴,
∴ ,
∴ ,
在中由勾股定理可得,
,
故答案为:.
(2)解:由(1)得,
, ,
∴ ,
故答案为.
24. (1)与
(2),
(3)根据根与系数的关系得,
∵,,
∴,,
即,
∴,
∴
.
25.(1)解:选小军采用了“截长法”(如图2),在上㵶取,使得,
证明:∵点M是的中点,
∴
∴,
在与中,
,
∴,
∴,
∵,即,
∴,
∴,
∴;
(2)解:①如图所示,直线l即为所作,
理由:∵点A与点D关于对称,
∴,,
∴,即,
∴F是的中点,
∵,,
∴,
由(1)得平分折线,
∴,
∵,
∴,
∴,
即l平分周长;
②由题意可得:,,,
由勾股定理,得,
∵,,
∴,
∴,即,
∴,
∴,
∴,
由①知周长
26.(1)解:连接,当,可得四边形为正方形,
此时可得:,
由此可得,若点为的“限角点”,则,
的半径为1,若为的“限角点”,则,
,,,
是的“限角点”,
故答案为:;
(2)解:点为的“限角点”时,,
设直线上有且只有一个的限角点,此时,,
直线的解析式为,则,
,
,
,
由勾股定理可得,即
解得或;
(3)解:∵圆心从原点出发,以个单位的速度沿直线:向上运动,
∴设移动后点坐标为,
设边上的点是的“限角点”,则,
移动的过程中,时,边上开始出现的“限角点”,
此时,解得,(舍去)
当时,边上开始出现的“限角点”;
当第一次移动到点或点在圆上时,边上最后一个的“限角点”消失,
此时,即,解得(舍去)或
∴时,边上存在的“限角点”;
当第二次移动到点在圆上时,三边上又开始出现的“限角点”,
,即,解得或(舍去)
即当时,三边上又要开始出现的“限角点”,
设直线的解析式为,则
解得,即,
设直线与直线的交点为,则
,解得
即,
当时,边上存在最后一个的“限角点”
即,解得,或(舍去)
当时,边上存在最后一个的“限角点”,
∴时,边上存在的“限角点”;
综上,当或,边上存在的“限角点”.
江苏省泰州市姜堰区张甸初级中学2022—2023学年上学期九年级第一次学情检测数学试卷: 这是一份江苏省泰州市姜堰区张甸初级中学2022—2023学年上学期九年级第一次学情检测数学试卷,共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
江苏省泰州市姜堰区四校联考2023届九年级下学期学情检测数学试卷(含答案): 这是一份江苏省泰州市姜堰区四校联考2023届九年级下学期学情检测数学试卷(含答案),共3页。
江苏省泰州市姜堰区2021-2022学年七年级下学期期末学情调查数学试卷(含解析): 这是一份江苏省泰州市姜堰区2021-2022学年七年级下学期期末学情调查数学试卷(含解析),共17页。试卷主要包含了若,则下列不等式成立的是,下列命题中,真命题是,___________等内容,欢迎下载使用。












