中考数学二轮专题复习《圆》解答题专项练习十（含答案）

这是一份中考数学二轮专题复习《圆》解答题专项练习十（含答案），共12页。
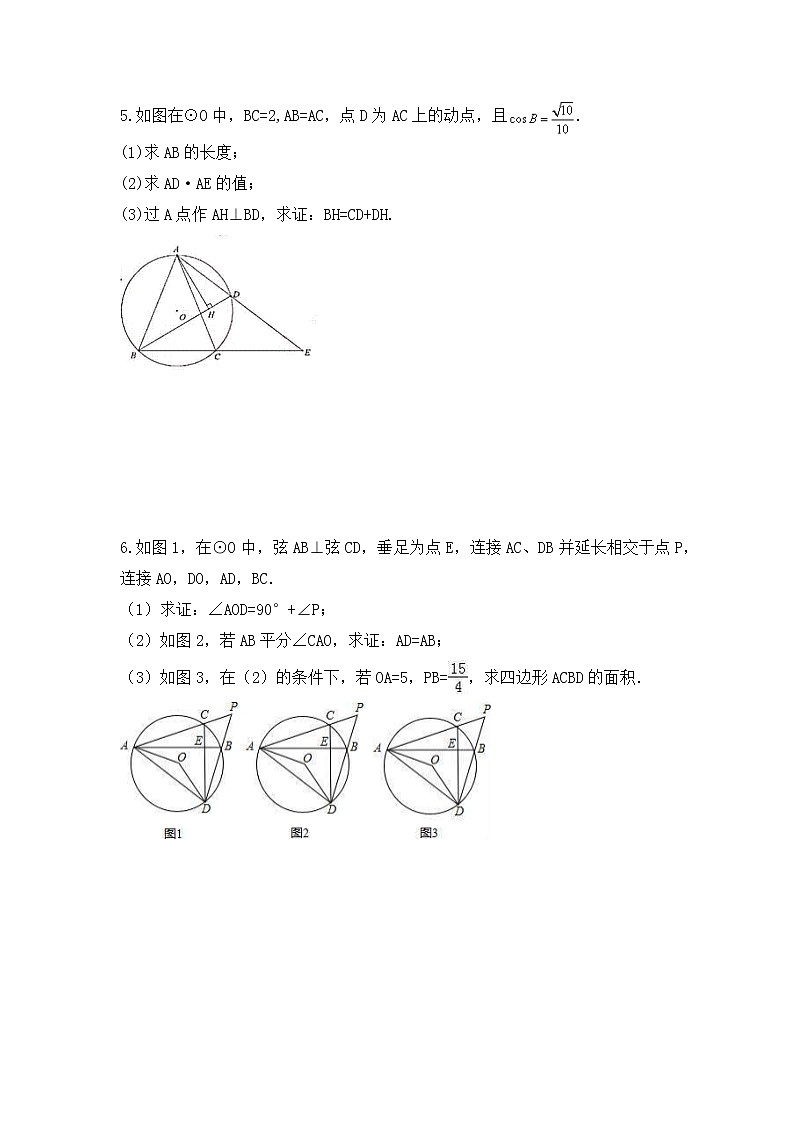
中考数学二轮专题复习《圆》解答题专项练习十1.如图，AB是⊙O的直径，弦CD⊥AB于点E，点F是⊙O上一点，且=，连接FB，FD，FD交AB于点N．（1）若AE=1，CD=6，求⊙O的半径；（2）求证：△BNF为等腰三角形；（3）连接FC并延长，交BA的延长线于点P，过点D作⊙O的切线，交BA的延长线于点M．求证：ON•OP=OE•OM．   2.在⊙O中,AB为直径,点P在AB延长线上,PC与⊙相切于C,点D为上点,且=,连AD．（1）如图1,求证：2∠A﹣∠P=90°；（2）如图2,延长AD、PC交于点E,若∠E=90°.求证：PC=AD；（3）如图3,延长AD、PC交于点E,点F在AO上,连接DF、CF,∠ECF=∠AFD﹣∠CFP,DF=2,AB=6,求线段CF的长.    3.如图，⊙O是△ABC的外接圆，点O在BC边上，∠BAC的平分线交⊙O于点D，连接BD、CD，过点D作BC的平行线与AC的延长线相交于点P．（1）求证：PD是⊙O的切线；（2）求证：AB•CP=BD•CD；（3）当AB=5cm，AC=12cm时，求线段PC的长．    4.如图，在边长为8的正方形ABCD中，点O为AD上一动点（4＜OA＜8），以O为圆心，OA的长为半径的圆交边CD于点E，连接OE、AE，过点E作⊙O的切线交边BC于F．（1）求证：△ODE∽△ECF；（2）在点O的运动过程中，设DE=x：①求OD•CF的最大值，并求此时⊙O的半径长；②判断△CEF的周长是否为定值？若是，求出△CEF的周长；否则，请说明理由？      5.如图在⊙O中，BC=2,AB=AC，点D为AC上的动点，且.(1)求AB的长度；(2)求AD·AE的值；(3)过A点作AH⊥BD，求证：BH=CD+DH.     6.如图1，在⊙O中，弦AB⊥弦CD，垂足为点E，连接AC、DB并延长相交于点P，连接AO，DO，AD，BC．（1）求证：∠AOD=90°+∠P；（2）如图2，若AB平分∠CAO，求证：AD=AB；（3）如图3，在（2）的条件下，若OA=5，PB=，求四边形ACBD的面积．      7.已知AB是⊙O的直径，AM和BN是⊙O的两条切线，DC与⊙O相切于点E，分别交AM、BN于D、C两点(1)如图1，求证：AB2=4AD·BC(2)如图2，连接OE并延长交AM于点F，连接CF．若∠ADE=2∠OFC，AD=1，求图中阴影部分的面积     8.如图,⊙O的半径r=25,四边形ABCD内接于圆⊙O，AC⊥BD于点H,P为CA延长线上的一点，且∠PDA=∠ABD．（1）试判断PD与⊙O的位置关系,并说明理由；（2）若tan∠ADB=，PA=AH,求BD的长；（3）在（2）的条件下,求四边形ABCD的面积．
0.参考答案1.解：（1）如图1，连接BC，AC，AD，∵CD⊥AB，AB是直径∴，CE=DE=CD=3∴∠ACD=∠ABC，且∠AEC=∠CEB∴△ACE∽△CEB∴∴∴BE=9∴AB=AE+BE=10∴⊙O的半径为5（2）∵=∴∠ACD=∠ADC=∠CDF，且DE=DE，∠AED=∠NED=90°∴△ADE≌△NDE（ASA）∴∠DAN=∠DNA，AE=EN∵∠DAB=∠DFB，∠AND=∠FNB∴∠FNB=∠DFB∴BN=BF，∴△BNF是等腰三角形（3）如图2，连接AC，CE，CO，DO，∵MD是切线，∴MD⊥DO，∴∠MDO=∠DEO=90°，∠DOE=∠DOE∴△MDO∽△DEO∴∴OD2=OE•OM∵AE=EN，CD⊥AO∴∠ANC=∠CAN，∴∠CAP=∠CNO，∵∴∠AOC=∠ABF∵CO∥BF∴∠PCO=∠PFB∵四边形ACFB是圆内接四边形∴∠PAC=∠PFB∴∠PAC=∠PFB=∠PCO=∠CNO，且∠POC=∠COE∴△CNO∽△PCO∴∴CO2=PO•NO，∴ON•OP=OE•OM．2.解：（1）如图1，连接OC，OD，∵PC是⊙O的切线，∴∠OCP=90°，∴∠POC=90°﹣∠P，∵=，∴∠AOD=∠POC，∴∠AOD=90°﹣∠P，∵OA=OD，∴∠A=∠ADO∴∠AOD+∠A+∠ADO=180°，∴90°﹣∠P+2∠A=180°，∴2∠A﹣∠P=90°，（2）如图2，连接OC，CD，∵PC是⊙O的切线，∴∠PCO=90°，∵∠E=90°，∴∠PCO=∠E，∴OC∥AC，∴∠POC=∠A，在Rt△POC中，∠P+∠POC=90°，∴∠A+∠P=90°，由（1）知，2∠A﹣∠P=90°，∴∠P=30°，∴PC=OC∵=，∴CD∥AB，∵OC∥AE，∴四边形AOCD是平行四边形，∴OC=AD，∴PC=AD；（3）如图3，过点C作CH⊥AB于M，连接CD，FH，DH，延长DF，PH相交于点N，连接CG，HG，∵CH⊥AB，∴∠FCH=∠FHC，∠CFB=∠HFB，∵∠ECF=∠AFD﹣∠CFP，∴∠GFH=∠ECH，∵PC，PH于⊙O相切，∴∠PCH=∠PHC，∴∠PCH+∠FCH=∠PHC+∠FHC，∴∠PCF=∠PHF，∴∠ECF=∠NHF，∵∠GFH=∠ECH，∴∠GFH=∠NHF，∴，∴CD∥AB，∴∠CMA=90°，∴∠DCH=90°，∴DH是⊙O的直径，∴∠DGH=90°∴∠FHG=90°﹣∠GFH=90°﹣∠FHN，∵DH是⊙O直径，∴∠DHN=90°，∴∠FHD=90°﹣∠FHN，∴∠FHG=∠FHD，∴，∵AB=DH=6，FD=2∴，∴HG=3GF，在Rt△DGH中，HG2+DG2=HD2，∴9GF2+（2+GF）2=36，∴GF=，∴FH==GF=．∵CH⊥HB，∴CF=FH=．3.（1）证明：连接OD．∵∠BAD=∠CAD，∴=，∴∠BOD=∠COD=90°，∵BC∥PA，∴∠ODP=∠BOD=90°，∴OD⊥PA，∴PD是⊙O的切线．（2）证明：∵BC∥PD，∴∠PDC=∠BCD．∵∠BCD=∠BAD，∴∠BAD=∠PDC，∵∠ABD+∠ACD=180°，∠ACD+∠PCD=180°，∴∠ABD=∠PCD，∴△BAD∽△CDP，∴=，∴AB•CP=BD•CD．（3）解：∵BC是直径，∴∠BAC=∠BDC=90°，∵AB=5，AC=12，∴BC==13，∴BD=CD=，∵AB•CP=BD•CD．∴PC==．4.解：（1）证明：∵EF切⊙O于点M，∴∠OEF=90°，∴∠OED+∠CEF=90°，∵∠C=90°，∴∠CEF+∠CFE=90°，∴∠OED=∠EFC，∵∠D=∠C=90°，∴△ODE∽△ECF；（2）解：①由（1）知：△ODE∽△ECF，∴=，∴OD•CF=DE•EC，∵DE=x，∴EC=8﹣x，∴OD•CF=x（8﹣x）=﹣x2+8x=﹣（x﹣4）2+16，当x=4时，OD•CF的值最大，最大值为16，设此时半径为r，则OA=OE=r，OD=8﹣r，在Rt△ODE中，∵OD2+DE2=OE2，∴（8﹣r）2+42=r2，解得r=5，即此时半径长为5；②△CEF的周长为定值，△CEF的周长=16，在Rt△ODE中，OD2+DE2=OE2，OA=OE，即：（8﹣OE）2+x2=OE2，∴OE=4+，OD=8﹣OE=4﹣，∵Rt△DOE∽Rt△CEF，即==，∴==，解得：CF=，EF=，∴△CEF的周长=CE+CF+EF=8﹣x++=16．5.解：6.解：（1）证明：∵AB⊥CD，∴∠AEC=90°，∴∠CAE+∠ACD=90°∵，∴∠CAE=∠CDB∵，∴∠AOD=2∠ACD，∵∠ACD=∠CDB+∠P∴∠AOD=∠ACD+（∠CDB+∠P）=∠ACD+∠CAE+∠P=90°+∠P；（2）如图1，延长AO交BD于点F，交CD于G，∵AB平分∠CAO，AB⊥CD，∴AC=AG，∴∠ACG=∠AGC，∵∠AGC=∠DGF，∠CAB=∠CDB，∴∠CAB+∠ACG=∠DGF+∠CDB，∴∠GFD=90°，由垂径定理可知：AF垂直平分线段BD，∴AB=AD；（3）过点O作OM⊥AB于点M，交AC于点H，连接HB，设∠CAB=α，∴由（2）可知：∠CAB=∠BAO=∠DAO=α，∴∠ACD=90°﹣α，∠PHB=2α，∠AOD=2∠ACD=2（90°﹣α）=180°﹣2α，由（1）可知：∠AOD=90°+∠P，∴∠PHB+∠P=2α+∠P=2α+∠AOD﹣90°=90°，由（2）可知：AH=AO，由垂径定理可知：AH=HB，∴HB=AO=5，∵PB=，∴由勾股定理可知：PH=，∵∠PHB=∠DAB=2α，∴tan∠PHB=tan∠DAB==，∴设AE=4m，ED=3m，∴由勾股定理可知：AD=5m，∵AB=AD=5m，∴EB=5m﹣4m=m，∵∠CDB=∠CAB，∴tan∠CDB=tan∠BAO==，∵由垂径定理可知：AM=AB=m，∴tan∠BAO=，tan∠CAE=，∴OM=，CE=，∴CD=m，∵由勾股定理可知：AO2=AM2+OM2，∴52=（m）2+（m）2，∴m=，∴四边形ACBD的面积为： AB•CE+AB•ED=AB•CD=m2=39．7.解：8.解：（1）PD与圆O相切．理由：如图，连接DO并延长交圆于点E，连接AE，∵DE是直径，∴∠DAE=90°，∴∠AED+∠ADE=90°，∵∠PDA=∠ABD=∠AED，∴∠PDA+∠ADE=90°，即PD⊥DO，∴PD与圆O相切于点D；（2）∵tan∠ADB=∴可设AH=3k，则DH=4k，∵PA=AH，∴PA=（4﹣3）k，∴PH=4k，∴在Rt△PDH中，tan∠P==，∴∠P=30°，∠PDH=60°，∵PD⊥DO，∴∠BDE=90°﹣∠PDH=30°，连接BE，则∠DBE=90°，DE=2r=50，∴BD=DE•cos30°=；（3）由（2）知，BH=﹣4k，∴HC=（﹣4k），又∵PD2=PA×PC，∴（8k）2=（4﹣3）k×[4k+（25﹣4k）]，解得：k=4﹣3，∴AC=3k+（25﹣4k）=24+7，∴S四边形ABCD=BD•AC=×25×（24+7）=900+．