高中数学人教B版 (2019)必修 第二册4.2.3 对数函数的性质与图像同步训练题

这是一份高中数学人教B版 (2019)必修 第二册4.2.3 对数函数的性质与图像同步训练题，共15页。试卷主要包含了函数，函数的值域为，已知，，，则的大小关系为，函数的图象必不过，已知则，若，则等内容，欢迎下载使用。
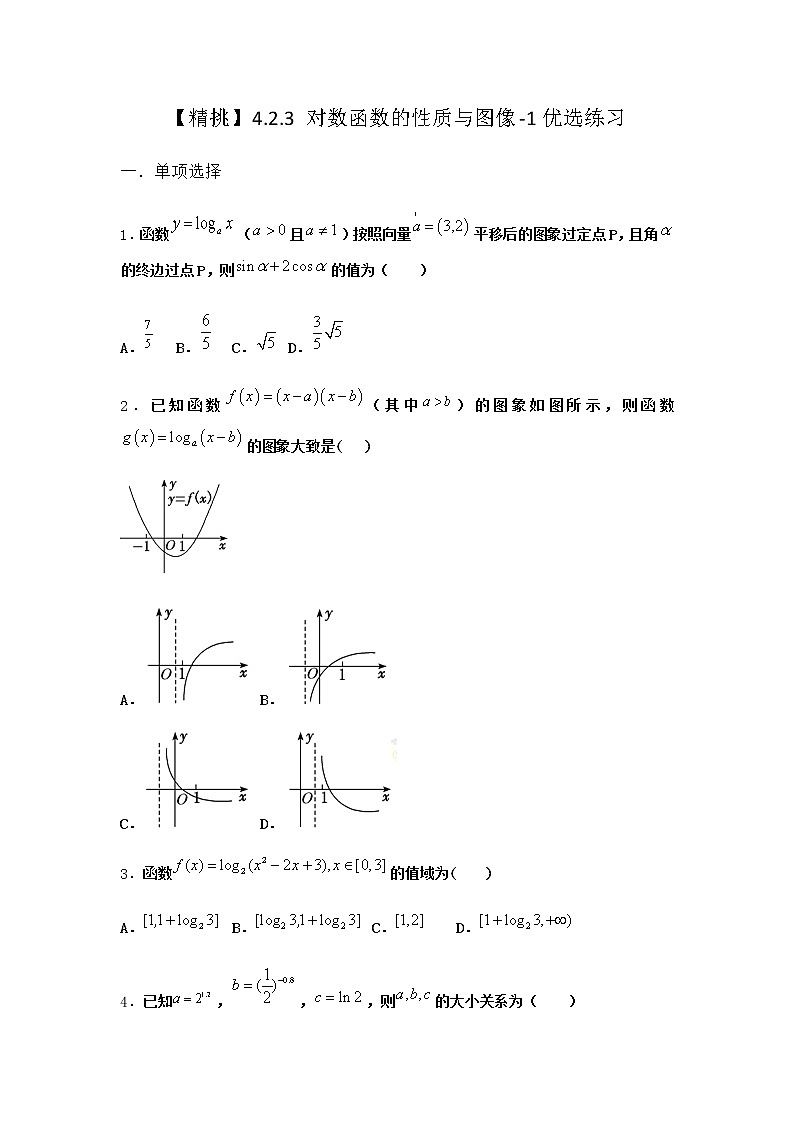
【精挑】4.2.3 对数函数的性质与图像-1优选练习一．单项选择1．函数（且）按照向量平移后的图象过定点P，且角的终边过点P，则的值为（    ）A． B． C． D．2．已知函数（其中）的图象如图所示，则函数的图象大致是(   )A． B．C． D．3．函数的值域为(    )A． B． C． D．4．已知，，，则的大小关系为（    ）A． B． C． D．5．函数的图象必不过（    ）A．第一象限 B．第二象限 C．第三象限 D．第四象限6．函数(，且)的图象恒过定点，且点在角的终边上，则（    ）A． B． C． D．7．已知函数,若,则实数的取值范围是(    )A． B． C． D．8．已知则（    ）A． B． C． D．9．若，则（    ）A．5 B．7 C．8 D．1010．设，，，则a，b，c的大小关系是（    ）A． B． C． D．11．若，，，则，，的大小关系为（    ）A． B． C． D．12．已知，那么（    ）A． B． C． D．13．某引进的外来水生植物在水面的蔓延速度极快，对当地的生态造成极大的破坏.某科研部门在水域中投放一定面积的该植物研究发现，该植物在水面的覆盖面积y（单位：）与经过的时间t（单位：月.）的关系为，则该植物在水域中的面积达到刚开始投放时的1000倍需要的时间（单位：月）为（　　）参考数据：.A．20 B．22 C．24 D．2614．若函数（且）有两个零点，则实数的取值范围是（    ）A． B． C． D．15．已知函数的单调递减区间是（    ）A． B． C． D．16．集合，，则等于（    ）A． B． C． D．17．若函数，其中．当时，有，则的值为（    ）A．6 B．9 C．18 D．2718．若函数（且）在区间上的最大值比最小值多2，则（    ）A．2或 B．3或 C．4或 D．2或
参考答案与试题解析1．【答案】C【解析】结合对数函数性质和三角函数平移法则可求得，再由三角函数定义求出对应计算即可详解：恒过，按向量平移后过定点，则，则故选：C【点睛】本题考查对数型函数过定点类问题，三角函数的基本定义，属于基础题2．【答案】B【解析】由二次函数的图像得到a＞1，即-1＜b＜0，再根据对数函数的性质即可得到答案．详解：法一：结合二次函数的图象可知，，，所以函数单调递增，排除C，D；把函数的图象向左平移个单位，得到函数的图象，排除A，选B.法二：结合二次函数的图象可知，，，所以，，在中，取，得，只有选项B符合，故选B.【点睛】本题考查函数的图象，对数函数的图象与性质和图象的平移变换.3．【答案】A【解析】先由二次函数的性质，求出内函数的值域，再由对数函数的性质，即可求出结果.详解：令，，因为是开口向上，对称轴为的二次函数，所以在上单调递减，在上单调递增；因此，，即；又函数单调递增，所以时，.故选：A.【点睛】本题主要考查求对数型复合函数的值域，熟记对数函数的性质，以及二次函数的性质即可，属于常考题型.4．【答案】D【解析】根据指数函数以及对数函数的性质判断即可．详解：a＝21.2＞2＞b＝（）﹣0.8＝20.8＞1＞c＝ln2，故a＞b＞c，故选D.【点睛】本题考查了指数函数以及对数函数的单调性问题，是一道基础题，解题关键是选择好中间量．5．【答案】A【解析】结合对数函数增减性和函数平移法则即可求解详解：由可判断为减函数，再根据函数平移法则，应由向左平移两个单位，如图，故的图象必不过第一象限故选：A【点睛】本题考查对数函数增减性的识别，函数图像平移法则，属于基础题6．【答案】C【解析】先根据对数函数性质得，进而根据正弦的二倍角公式和三角函数的定义求解即可得答案.详解：解：根据对数函数的性质得函数(，且)的图象恒过，由三角函数的定义得：，，所以根据二倍角公式得：.故选：C.【点睛】本题考查对数函数性质，三角函数定义，正弦的二倍角公式，考查运算能力，是中档题.7．【答案】B【解析】先计算函数的定义域,再根据的单调性与奇偶性求解即可.详解：由题的定义域满足,解得.又,故为奇函数.又,且在为减函数,故在为减函数.故为减函数.故即.所以,解得.故选：B【点睛】本题主要考查了根据函数的奇偶性与单调性求解不等式的问题,需要根据题意判断函数的奇偶性与单调性,并结合定义域进行求解,属于中档题.8．【答案】A【解析】根据对数函数与指数函数的单调性,将与0．1比较,即可得出答案.详解：因为在上单调递增,所以,因为在上单调递减,所以,因为在上单调递增,所以,所以.故选：A【点睛】本题考查指数与指数函数和对数与对数函数.属于基础题.本类题型一般都是将所需比较的数与0．1比较大小,熟练掌握指数函数与对数函数的单调性是解本题的关键.9．【答案】C【解析】分析：由，得到求解.详解：因为，所以，即，所以故选：C10．【答案】A【解析】分析：根据对数函数的单调性结合不等式的性质可判断.详解：，，，即，，，即，.故选：A.11．【答案】D【解析】分析：先与1比较，再与比较，即可判断大小.详解：因此故选：D【点睛】本题考查比较大小．指数函数单调性．对数函数单调性，考查基本分析判断能力，属基础题.12．【答案】B【解析】分析：先利用指数函数单调性判断b，c和1大小关系，再判断a与1的关系，即得结果.详解：因为在单调递增，，故，即，而，故.故选：B.13．【答案】C【解析】分析：首先求刚开始投放的面积，再根据公式求解的值.详解：刚投放时的面积为，设经过t个月该植物在水域中的面积是刚开始投放时的1000倍，则，.故选：C14．【答案】B【解析】将函数（且）有两个零点转化为函数和函数图象有两个交点问题，然后分类讨论和进行判断即可得出答案.详解：当函数（且）有两个零点，则若， 有两个根，则得函数和函数图象有两个交点，①当时，因为函数的图象恒过点(1,0)，而直线的图象恒过点，由于，则点一定在点(1,0)的右侧，如图所示：由图象可知，当时，函数与的图象有两个交点，即时函数有两个零点；②当时，函数与的图象仅有一个交点，如图所示：此时函数有且仅有一个零点；综上可得满足题意.故选：B.【点睛】本题考查了分类讨论思想和数形结合思想的应用，考查了函数零点个数的问题，属于中档题.15．【答案】C【解析】先求函数的定义域，再根据复合函数单调性之间的关系判断即得.详解：由，得或，的定义域为.令，则函数在上单调递减，在上单调递增.又函数在上是减函数，由复合函数单调性之间的关系可得，函数的单调递减区间是.故选：.【点睛】本题考查复合函数的单调性，注意函数的定义域，属于中档题.16．【答案】C【解析】分析：利用对数函数．指数函数的单调性求出集合，再由集合的交运算即可求解.详解：，，所以.故选：C17．【答案】D【解析】分析：首先画出函数的图象，再根据条件代入，最后根据对数运算，化简求值.详解：，得，得，如图，，得，即，化简得，即，即.故选：D【点睛】关键点点睛：本题考查函数新定义，关键是画出函数的图象，利用函数图象确定，的值.18．【答案】A【解析】分别讨论和，然后利用对数函数的单调性，代入计算即可得出答案.详解：①当时，函数在定义域内为增函数，则由题意得，解得；②当时，函数在定义域内为减函数，则由题意得，解得；综上可得：或.故选：A.【点睛】本题考查了分类讨论思想的应用，考查了对数函数单调性的应用，属于一般难度的题.