天津市宝坻区第四中学2022-2023学年高二下学期数学周测卷1

这是一份天津市宝坻区第四中学2022-2023学年高二下学期数学周测卷1，文件包含选择性必修第二册高二第二学期--周测01解析版docx、选择性必修第二册高二第二学期--周测01原卷版docx等2份试卷配套教学资源，其中试卷共12页， 欢迎下载使用。
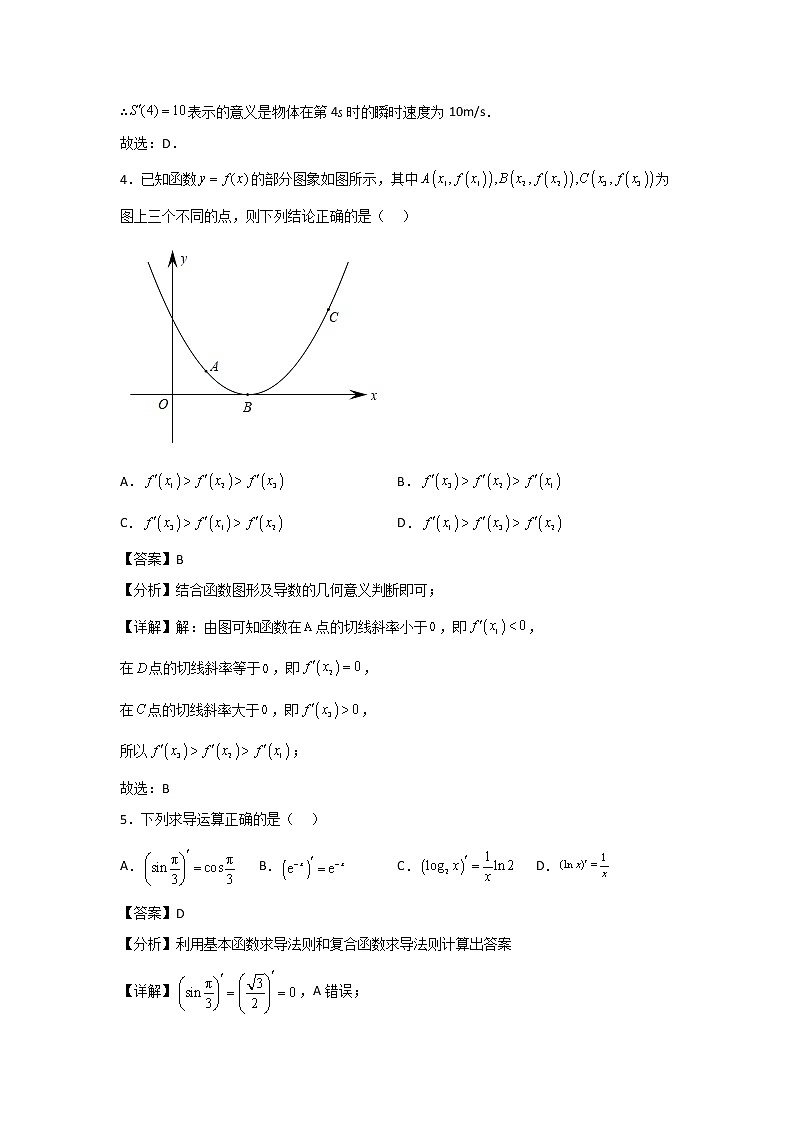
高二数学第二学期---周测01一、单选题1．函数在区间上的平均变化率为（    ）A．2 B．3 C．5 D．4【答案】C【分析】根据平均变化率的知识求得正确答案.【详解】当时，；当时，.所以函数在区间上的平均变化率为.故选：C2．设函数在处的导数为2，则（    ）A．2 B．1 C． D．6【答案】A【分析】根据导数的定义即得.【详解】因为函数在处的导数为2，所以.故选：A.3．已知物体做直线运动对应的函数为，其中S表示路程，t表示时间．则＝10表示的意义是（　　）A．经过4s后物体向前走了10mB．物体在前4秒内的平均速度为10 m/s C．物体在第4秒内向前走了10mD．物体在第4秒时的瞬时速度为10m/s【答案】D【分析】根据导数的物理意义可知，函数的导数即是t时刻的瞬时速度．求解即可．【详解】∵物体做直线运动的方程为，根据导数的物理意义可知，函数的导数是t时刻的瞬时速度，∴表示的意义是物体在第4s时的瞬时速度为10m/s．故选：D．4．已知函数的部分图象如图所示，其中为图上三个不同的点，则下列结论正确的是（    ）A． B．C． D．【答案】B【分析】结合函数图形及导数的几何意义判断即可；【详解】解：由图可知函数在点的切线斜率小于，即，在点的切线斜率等于，即，在点的切线斜率大于，即，所以；故选：B5．下列求导运算正确的是（    ）A． B． C． D．【答案】D【分析】利用基本函数求导法则和复合函数求导法则计算出答案【详解】，A错误；，B错误；，C错误；，D正确.故选：D6．曲线在点处的切线的倾斜角为（     ）A． B． C． D．【答案】A【分析】根据导数的几何意义得到点处切线的斜率，再根据斜率求倾斜角即可.【详解】，所以在点处的切线的斜率为-1，倾斜角为.故选：A.7．已知某容器的高度为30cm，向容器内注入液体，且容器内液体的高度h（单位：cm）与时间t（单位：s）的函数关系式为．当时，液体上升高度的瞬时变化率为2e cm/s，则当时，液体上升高度的瞬时变化率为（    ）A． B． C． D．【答案】C【分析】根据导数的实际意义求解即可.【详解】，当时，，解得，故.当时，液体上升高度的瞬时变化率为．故选：C8．已知，则（    ）A． B． C． D．【答案】B【分析】求导得到导函数，计算，再代入计算得到答案.【详解】，则，，解得.，.故选：B二、填空题9．已知函数为其导函数，则__________.【答案】##【分析】对函数求导，即可求出的值.【详解】因为，故.故答案为：.10．曲线在点处的切线方程为______.【答案】【分析】根据导数的几何意义即得.【详解】因为，所以，，又，所以曲线在点处的切线方程为，即.故答案为：.11．若函数的图象在点处的切线恰好经过点（2，3），则a＝______．【答案】-1【分析】先求导，然后分别求出，表示出切线方程，最后将点（2，3）代入切线方程即可求出答案.【详解】由题可知，则．又，所以的图象在点处的切线方程为，即．因为点（2，3）在切线上，所以，解得．故答案为：-1.12．已知直线是函数与函数的公切线，若是直线与函数相切的切点，则____________．【答案】【分析】求出导函数，，由得切线方程，设图象上的切点为，由导数几何意义得切线方程，两直线重合求得，从而得值．【详解】，，又，所以切线的方程为，即，设直线与相切的切点为，，所以切线方程为，即，所以，解得，所以．故答案为：．三、解答题13．求下列函数的导数.(1)；(2).【答案】(1)(2) 【分析】由常见函数的导数公式及导数的运算法则可得答案.【详解】（1）（2）14．已知曲线.(1)求曲线在点处的切线方程；(2)求满足斜率为1的曲线的切线方程.【答案】(1)(2)和. 【分析】（1）对曲线求导,求出点处切线的斜率,再求出切线方程;（2）设切点为,由曲线的切线斜率为1,求出切点坐标,再求出切线方程.【详解】（1）由,得，∴在点处切线的斜率.∴曲线在点处的切线方程为，即.（2）设切点为，则切线的斜率为.曲线的切线斜率为1,,解得，切点为，.切线方程为和，即和.15．已知，且(1)求的值；(2)求在处的切线方程．【答案】(1)0(2) 【分析】（1）求导，代入，列出方程，求出；（2）在（1）的基础上，求出，，利用点斜式求出切线方程，化为一般式即可.【详解】（1），则，解得：；（2）由（1）知，，故，，所以在处的切线方程为，即.16．已知曲线．(1)若曲线在点处的切线与直线平行且距离为，求直线的方程；(2)求与曲线相切，并过点的直线方程．【答案】(1)或．(2) 【分析】（1）由导数求得切线斜率，设出直线方程，再由点到直线的距离公式得参数值，得直线方程；（2）设切点坐标为，由导数的几何意义求得切线方程，利用切线过点得，得切线方程．(1)由题意，，切线与直线平行，设直线方程为，所以，解得或，所以直线方程为或．(2)设切点为，则，又，所以切线方程为，切线过点，所以，解得，所以切线方程是，即．