高中数学人教B版 (2019)选择性必修 第一册1.2.3 直线与平面的夹角达标测试

这是一份高中数学人教B版 (2019)选择性必修 第一册1.2.3 直线与平面的夹角达标测试，共19页。
1.2.3 直线与平面的夹角一、    概念练习1.如图,正四棱锥中，O为顶点在底面内的投影，P为侧棱SD的中点，且，则直线BC与平面PAC的夹角是(   )

A．30° B．45° C．60° D．90°2.正四棱锥中，，则直线AC与平面SBC所成角的正弦值为()A. B. C. D.3.如图，在正三棱柱中，，，D是的中点，则AD与平面所成角的正弦值等于(   )

A. B. C. D.4.如图,在棱长为1的正方体中,为的中点,则直线与平面的夹角为()A. B. C. D.5.在正三棱柱中,已知,D在棱上,且,则AD与平面所成的角的正弦值为(   )
A. B. C. D.二、能力提升6.已知正三棱柱的侧棱长与底面边长相等,则与侧面所成角的正弦值为(   )
A. B. C. D.7.在正方体中，E是的中点，则直线BE与平面所成角的正弦值为(   )
A. B. C. D.8.（多选）若将正方形ABCD沿对角线BD折成直二面角，则下列结论正确的有(   )
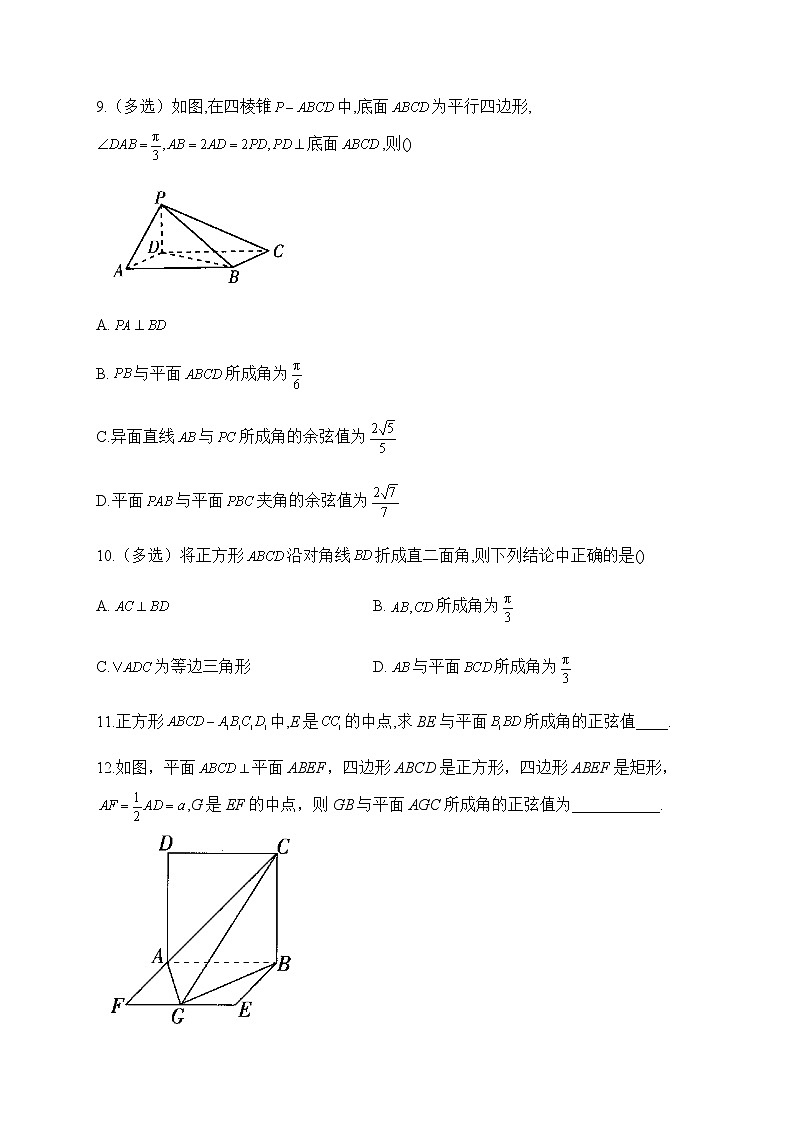
A.AD与BC所成的角为45°B.AC与BD所成的角为90°C.BC与平面ACD所成角的正弦值为D.平面ABC与平面BCD的夹角的正切值是9.（多选）如图,在四棱锥中,底面为平行四边形,底面,则()A.B.与平面所成角为C.异面直线与所成角的余弦值为D.平面与平面夹角的余弦值为10.（多选）将正方形沿对角线折成直二面角,则下列结论中正确的是()A.  B.所成角为C.为等边三角形 D.与平面所成角为11.正方形中,E是的中点,求BE与平面所成角的正弦值____.12.如图，平面平面ABEF，四边形ABCD是正方形，四边形ABEF是矩形，,G是EF的中点，则GB与平面AGC所成角的正弦值为___________.
 13.已知向量分别是直线的方向向量和平面的法向量.若,则与所成角的大小为_______________.14.在四棱锥中，底面ABCD，，，，.（1）证明：；（2）求PD与平面PAB所成的角的正弦值.15.如图，已知三棱柱，平面平面ABC，，，，E，F分别是AC，的中点.（1）证明：；（2）求直线EF与平面所成角的余弦值.


 
答案以及解析1.答案：A解析：如图所示,以为原点建立空间直角坐标系Oxyz.设，则.则，设平面的法向量为,则，可求得，则.∴，∴直线与平面所成的角为.故选A.2.答案：C解析：连接BD，AC，交于点O，连接OS，则平面ABCD，，建立如图所示的空间直角坐标系，则，，，，所以，，设平面SBC的法向量为，则由，，得令，得，，所以.又，设直线AC与平面SBC所成角为，则.故选C.3.答案：B解析：以C为原点，建立如图所示的空间直角坐标系，

则，，，，
所以，，.
设平面的一个法向量为，
则
取，得.
设AD与平面所成的角为，
则，
所以AD与平面所成角的正弦值为.故选B.4.答案：B解析：以点为原点,分别为x轴、y轴、z轴的正方向建立空间直角坐标系,

则,,.
设平面的一个法向量.则即令，则，，平面BDE的一个法向量为.，.又，，直线与平面BDE的夹角为.故选B.5.答案：A解析：取AC的中点E，连接BE，则，如图，建立空直角坐标系Bxyz，则，，则.平面平面, ，平面, 为平面的一个法向量.设AD与平面所成的角为，则,故选A.
 6.答案：A解析：建立如图所示的空间直角坐标系（O为AC的中点）.
设正三棱柱的侧棱长为2，则，，，，所以，.又为侧面的一个法向量，所以.
 7.答案：B解析：建立如图所示的空间直角坐标系，设正方体的棱长为2，则，则.设平面的法向量为.因为，所以,即设，令，则为平面的一个法向量.于是，则直线BE与平面所成角的正弦值为.
 8.答案：BCD解析：取BD的中点O，连接AO,CO.
若将正方形ABCD沿对角线BD折成直二面角，则,,，
以O为原点，OC所在直线为x轴，OD所在直线为y轴，OA所在直线为z轴，建立如图所示的空间直角坐标系.

设，则，，，，
，，
，
AD与BC所成的角为60°，故A不正确；
易得，，
，，故B正确；
设平面ACD的一个法向量为，
则取，则，
，
设BC与平面ACD所成的角为，
，故C正确；
易知平面BCD的一个法向量，
，，
设平面ABC的一个法向量为，
则取，则，
，，
设平面ABC与平面BCD的夹角为，
则，
，，
平面ABC与平面BCD所成角的正切值是，故D正确.故选BCD.9.答案：ABCD解析：对于A,由及余弦定理得,从而,故.由底面,可得.又,所以平面,故.故A正确.对于B,因为底面,所以就是与平面所成的角,又,所以.故B正确.对于C,显然是异面直线与所成的角,易得.故C正确.对于D,以为坐标原点,建立如图所示的空间直角坐标系.设,则,所以.设平面的法向量为,则,即,取,可得是平面的一个法向量.设平面的法向量为,则,即,取,可得是平面的一个法向量,所以,所以平面与平面夹角的余弦值为.故D正确.10.答案：ABC解析：如图,A.取中点为,连接,易知平面,故.B.以为坐标原点,建立空间直角坐标系如图所示,设正方形边长为,则,故.由两向量夹角公式得,故异面直线所成的角为.C.在直角三角形中,由,得,故为等边三角形.D.易知即为直线与平面所成的角,易得,故D错误.11.答案：解析：以D为原点，建立空间直角坐标系,设正方体的棱长为2,则,,,所以,,.设平面的法向量为,则即令,则,所以.设直线BE与平面所成的角为，则.12.答案：解析：由于平面平面ABEF，四边形ABCD是正方形，四边形ABEF是矩形，故AF,AB,AD两两互相垂直，以A为原点，，, 的方向分别为x轴，y轴，z轴的正方向建立空间直角坐标系，如图所示，

则，，，，所以，，，
设平面AGC的一个法向量为，则
令，得，
因此GB与平面AGC所成角的正弦值为.
13.答案：60°解析：设与所成角为,则.14.答案：（1）证明见解析（2）解析：解：（1）如图所示，取AB中点为O，连接DO，CO，则.

又，所以四边形DCBO为平行四边形.
又，
所以四边形DCBO为菱形，所以.
同理可得，四边形DCOA为菱形，所以，
所以.
因为底面ABCD，底面ABCD，所以，
又，平面ADP，所以平面ADP.
因为平面ADP，所以.（2）由（1）知，又，所以，
所以三角形ADO为正三角形.
过点D作垂直于DC的直线为x轴，DC所在直线为y轴，DP所在直线为z轴，建立如图所示的空间直角坐标系，
 则，，，.
则，，.
设平面PAB的法向量为，
则.
令，则，，所以.
设直线PD与平面PAB所成的角为，
则，
所以直线PD与平面PAB所成的角的正弦值为.15.答案：（1）证明见解析（2）解析：（1）解法一：证明：连接，因为，E是AC的中点，所以，
又平面平面ABC，平面，平面平面，
所以平面ABC，
则.又因为，，
所以.
因为，
所以平面.
因此.

解法二：证明：连接，因为，E是AC的中点，所以.
又平面平面ABC，平面，平面平面，
所以平面ABC.
如图，以E为原点，分别以射线EC，为y，z轴的正半轴，建立空间直角坐标系Exyz.

不妨设，则，，，，，.
因此，，
.
由得.
（2）解法一：取BC的中点G，连接EG，GF，则四边形是平行四边形.
由于平面ABC，故，
所以平行四边形为矩形.
由（1）得平面，则平面平面，所以EF在平面上的射影在直线上.
连接交EF于O，则是直线EF与平面所成的角（或其补角），
不妨设，则在中，，.
由于O为的中点，故，
所以.
因此，直线EF与平面所成角的余弦值是.
解法二：由（1）可得.
设平面的法向量为.
由
得
取，则，
设直线EF与平面所成角为，
则.
因此，直线EF与平面所成角的余弦值为.