

所属成套资源:全套人教B版高中数学选择性必修第一册优选作业含答案
人教B版 (2019)选择性必修 第一册2.7.2 抛物线的几何性质练习
展开
这是一份人教B版 (2019)选择性必修 第一册2.7.2 抛物线的几何性质练习,共15页。试卷主要包含了若,则的最小值是_______,已知抛物线等内容,欢迎下载使用。
【精挑】2.7.2 抛物线的几何性质优选练习一.填空题1.若,则的最小值是_______.2.已知为抛物线的焦点,为上一点,为到原点的距离,若,则_________.3.已知抛物线的焦点为,准线为,过点且斜率为的直线交抛物线于点(在第一象限),,垂足为,直线交轴于点,则_____________.4.已知抛物线:的准线方程为,焦点为,准线与轴的交点为,为抛物线上一点,且满足,则______.5.抛物线上一点到焦点的距离为,则点的纵坐标为______________.6.已知抛物线的焦点为F,其准线与双曲线相交于A,B两点.若为直角三角形,则抛物线的准线方程为________.7.已知倾斜角为的直线过曲线的焦点,且与相交于不同的两点(在第一象限),则_____.8.抛物线的焦点为,点,为抛物线上一点,且不在直线上,则周长的最小值为____.9.已知点为抛物线上的点,且点P到抛物线C焦点的距离为3,则___________.10.中国古代桥梁的建筑艺术,有不少是世界桥梁史上的创举,充分显示了中国劳动人民的非凡智慧.一个抛物线型拱桥,当水面离拱顶2m时,水面宽8m.若水面下降1m,则水面宽度为______.11.抛物线的焦准距是______.12.已知抛物线,圆心在上的圆过原点且与抛物线的准线相切,若该圆截直线所得弦长为,则的方程为___________.13.抛物线的焦点为F,准线L与x轴交于点M,若N为L上一点,当为等腰三角形,时,则_______.14.已知点是抛物线上的一个动点,则点到点的距离与到抛物线的准线的距离之和的最小值为___________.15.已知抛物线C:y2=4x的焦点为F,准线为l,P为C上一点,PQ垂直l于点Q,M,N分别为PQ,PF的中点,MN与x轴相交于点R,若∠NRF=60°,则|FR|等于_____.
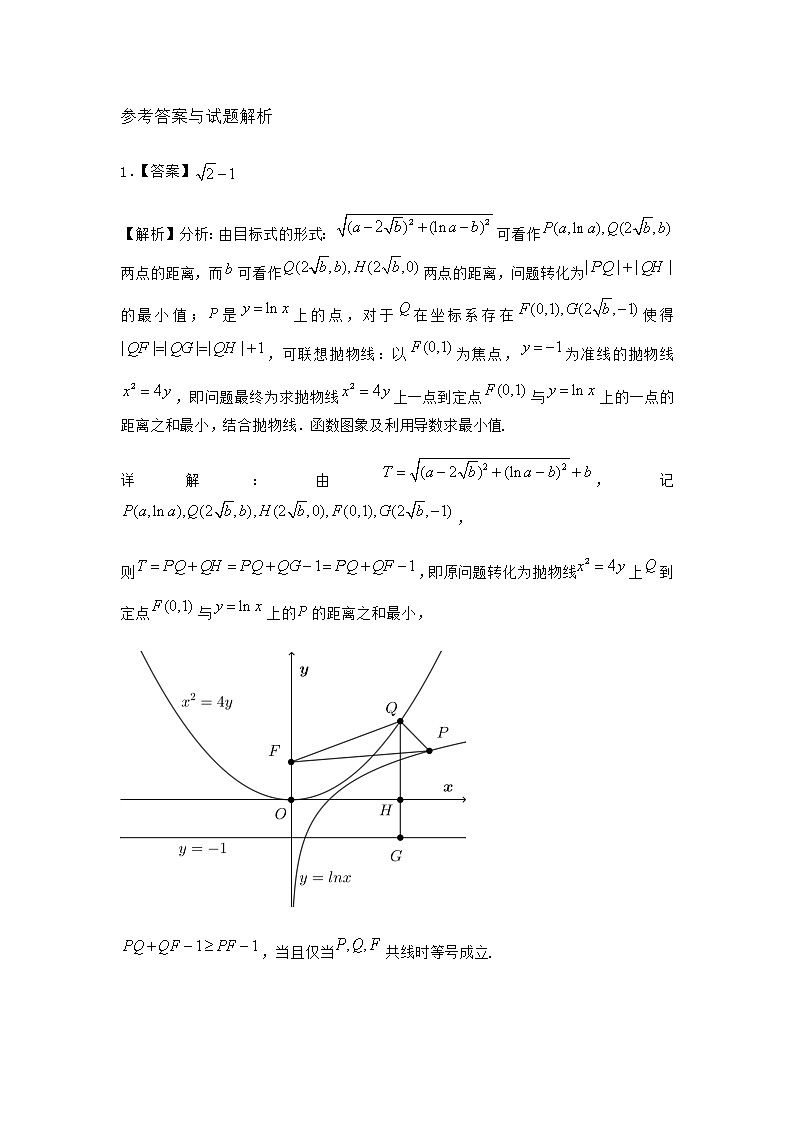
参考答案与试题解析1.【答案】【解析】分析:由目标式的形式:可看作两点的距离,而可看作两点的距离,问题转化为的最小值;是上的点,对于在坐标系存在使得,可联想抛物线:以为焦点,为准线的抛物线,即问题最终为求抛物线上一点到定点与上的一点的距离之和最小,结合抛物线.函数图象及利用导数求最小值.详解:由,记,则,即原问题转化为抛物线上到定点与上的的距离之和最小,,当且仅当共线时等号成立.令,则且,由于单调增,则是唯一零点,即有在上单调递减,在上单调递增,则,即最小值为.则.故答案为:.【点睛】本题考查了利用几何法求代数式的最值,综合抛物线的性质.两点距离公式.数形结合.导数研究函数最值的应用,属于难题.2.【答案】或3【解析】分析:由已知得,即,再由抛物线的定义,得,可求得答案.详解:因为为上一点,所以,即,由抛物线的定义,得,整理得,故或3.故答案为:或3.【点睛】本题考查抛物线的定义和几何性质,属于基础题.3.【答案】【解析】分析:由抛物线定义知,再由题意可得为等边三角形,为的中点,可得为三角形的中位线,可得为的中点,为等边角形的高,由中,可得的值,进而求出的值.详解:如图所示设准线与轴交于.易知,,由抛物线定义知.由题意,,为等边三角形,,.又是的中位线,就是该等边的高,.故答案为:.【点睛】本题考查抛物线的性质及直线与抛物线的位置关系,属于中档题.4.【答案】【解析】分析:由求出,可得抛物线方程为,利用抛物线的定义可求出,再利用余弦定理可得答案.详解:由题可知:抛物线:,准线方程,则,有,∴,∴抛物线方程为::,∵,作准线,交于点,由抛物线的定义得:,∴,设,则,∴,在三角形中,,,,由余弦定理可得,解得,故答案为:【点睛】与焦点.准线有关的问题一般情况下都与拋物线的定义有关,解决这类问题一定要注意点到点的距离与点到直线的距离的转化:(1)将抛线上的点到准线距离转化为该点到焦点的距离;(2)将抛物线上的点到焦点的距离转化为到准线的距离,使问题得到解决.5.【答案】2【解析】分析:求出抛物线的标准方程以及抛物线的准线,根据抛物线的定义可得点到准线的距离为,从而求解.详解:抛物线方程改写为,根据抛物线的定义,知点到准线的距离也为,所以的纵坐标为.故答案为:26.【答案】【解析】分析:先求出准线方程为,代入双曲线方程可得A,B的坐标,再由为直角三角形,设中点为,则,即,进而求解.详解:由题可知准线方程为,因为与双曲线相交于A,B,则为,为,因为为直角三角形,由双曲线的对称性可得,设中点为,则,即,解得,即,所以准线方程为,故答案为:【点睛】本题考查抛物线的几何性质,考查双曲线的方程的应用,考查运算能力.7.【答案】【解析】分析:求出点坐标,过作垂直轴于点,垂直准线于点,为准线与轴的交点,由结合直线倾斜角是60°可得出的方程,从而求得.详解:由曲线即得,.过作垂直轴于点,垂直准线于点,为准线与轴的交点,则,所以.故答案为:.【点睛】本题考查抛物线的焦点弦问题,考查求抛物线上的点到焦点的距离,解题关键利用抛物线的定义建立焦半径的关系式.8.【答案】【解析】分析:求△MAF周长最小值,即求|MA|+|MF|的最小值.设点M在准线上的射影为D,根据抛物线定义知|MF|=|MD|,转为求|MA|+|MD|的最小值,当D.M.A三点共线时|MA|+|MD|最小,即可得到答案.详解:求△MAF周长的最小值,即求|MA|+|MF|的最小值,设点M在准线上的射影为D,则根据抛物线的定义,可知|MF|=|MD|因此,|MA|+|MF|的最小值,即|MA|+|MD|的最小值根据平面几何知识,可得当D,M,A三点共线时|MA|+|MD|最小,因此最小值为xA﹣(﹣1)=2+1=3,∵|AF|==,∴△MAF周长的最小值为3+,故答案为3+ 【点睛】本题考查抛物线的定义.标准方程,以及简单性质的应用,判断当D,M,A三点共线时|MA|+|MD|最小,是解题的关键.9.【答案】【解析】分析:根据抛物线的焦半径公式求解,再由于点在抛物线上,点的坐标满足抛物线的方程,得到.详解:设抛物线的焦点为,则,根据抛物线的焦半径公式可知:,所以,代入抛物线方程得到:,故.故答案为:.【点睛】本题主要考查抛物线的定义,抛物线上的点到焦点的距离等于其到准线的距离,从而得到焦半径公式,平时做题时也要特别注意定义的应用.10.【答案】【解析】分析:以拱桥顶点为原点,建立直角坐标系,设抛物线方程根据题意可得答案.详解:由题意,以拱桥顶点为原点,建立直角坐标系,设抛物线方程,由题意知,抛物线经过点和点,代入抛物线方程解得,,所以抛物线方程,水面下降1米,即,解得,,所以此时水面宽度.故答案为:.11.【答案】【解析】分析:抛物线化为标准方程,即可求得抛物线焦点到准线的距离.详解:解:抛物线化为标准方程为...抛物线的焦准距是.故答案为:.【点睛】本题考查抛物线的标准方程与几何性质,解题关键是理解焦准距的含义,属于基础题.12.【答案】【解析】分析:由题,得圆心坐标,所以P到的距离,又由,列出方程解得p,即可得到本题答案.详解:如图,设圆心为,因为,所以,且,则P到的距离,又由,得,所以抛物线的标准方程为.故答案为:【点睛】本题主要考查抛物线与圆的综合问题,考查学生分析问题和解决问题的能力,以及运算求解能力.13.【答案】2【解析】分析:根据抛物线的方程求出焦点F的坐标和准线L的方程及的坐标,根据N为L上一点且为等腰三角形得到为等腰直角三角形,根据勾股定理求出的长度即为的值.详解:解:根据抛物线方程得到焦点,准线L的方程为,所以,则 ,又因为为等腰三角形,N为L上一点得到为等腰直角三角形,即,又斜边 ,根据勾股定理求出,则.故答案为: 2【点睛】本题要求学生掌握抛物线的简单性质,灵活运用勾股定理解直角三角形.是一道基础题.14.【答案】【解析】分析:设点在抛物线的准线的投影为点,抛物线的焦点为,根据抛物线的定义可得,再根据三角形的性质:即可求解.详解:设点在抛物线的准线的投影为点,抛物线的焦点为,则.依抛物线的定义,知点到该抛物线的准线的距离为,则点到点的距离与到该抛物线的准线的距离之和.故答案为:.15.【答案】2【解析】分析:由题意知:,,,.由∠NRF=60°,可得为等边三角形,MF⊥PQ,可得F为HR的中点,即求.详解:不妨设点P在第一象限,如图所示,连接MF,QF.∵抛物线C:y2=4x的焦点为F,准线为l,P为C上一点∴,.∵M,N分别为PQ,PF的中点,∴,∵PQ垂直l于点Q,∴PQ//OR,∵,∠NRF=60°,∴为等边三角形,∴MF⊥PQ,易知四边形和四边形都是平行四边形,∴F为HR的中点,∴,故答案为:2.【点睛】本题主要考查抛物线的定义,属于基础题.
相关试卷
这是一份数学选择性必修 第一册2.7.2 抛物线的几何性质达标测试,共14页。试卷主要包含了设抛物线等内容,欢迎下载使用。
这是一份高中数学人教B版 (2019)选择性必修 第一册第二章 平面解析几何2.7 抛物线及其方程2.7.2 抛物线的几何性质课堂检测,共12页。
这是一份数学选择性必修 第一册2.7.2 抛物线的几何性质复习练习题,共11页。试卷主要包含了在平面直角坐标系中,若双曲线等内容,欢迎下载使用。









