

高中数学人教B版 (2019)选择性必修 第一册第二章 平面解析几何2.2 直线及其方程2.2.2 直线的方程同步测试题
展开【精品】2.2.2 直线的方程-2随堂练习
一.填空题
1.过点且和原点距离为1的直线方程为______.
2.已知两条平行直线:与:的距离为,则______.
3.若直线与直线互相垂直,那么的值等于__________.
4.已知过点和的直线与直线平行,则的值为______.
5.平面直角坐标系中,点.的坐标分别为.,则线段的垂直平分线方程为(用一般式表示)________.
6.已知直线过点,且与直线平行,则直线的方程为__.
7.已知两条直线,若的一个法向量恰为的一个方向向量,则___________
8.已知直线与直线垂直,则的值为__________.
9.已知直线和.若,则实数__________,两直线与间的距离是__________.
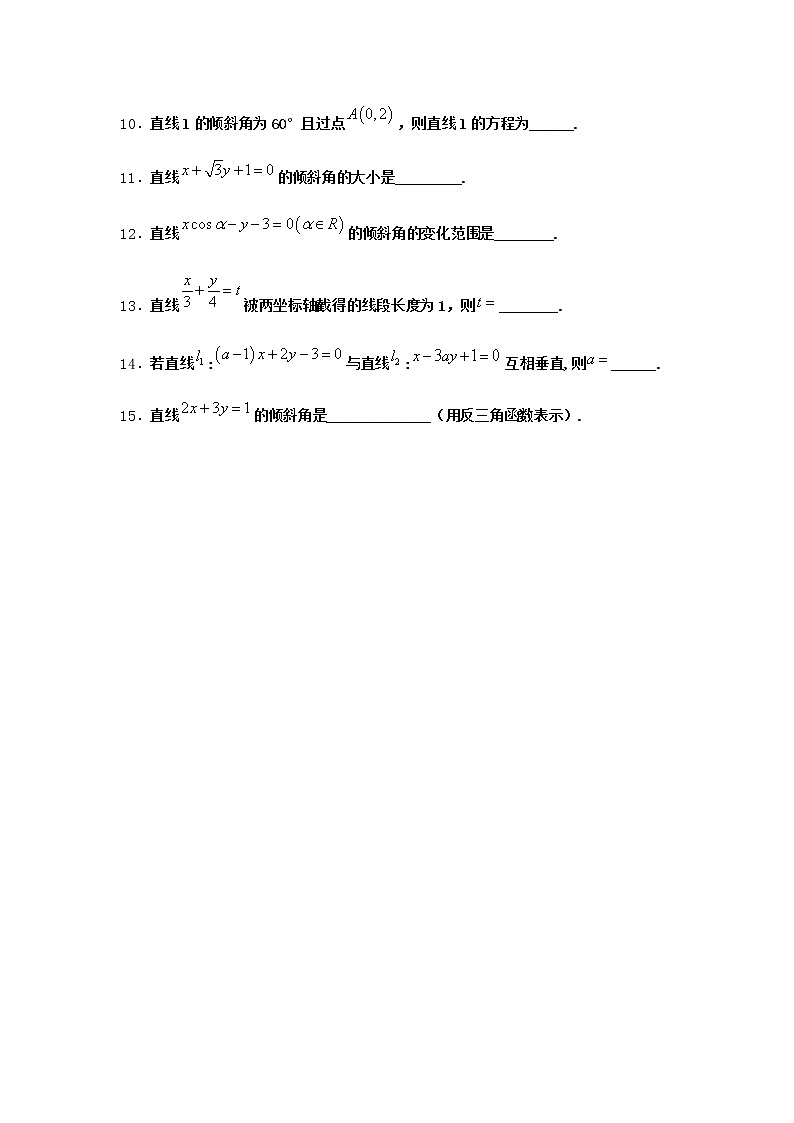
10.直线l的倾斜角为60°且过点,则直线l的方程为______.
11.直线的倾斜角的大小是_________.
12.直线的倾斜角的变化范围是________.
13.直线被两坐标轴截得的线段长度为1,则________.
14.若直线:与直线:互相垂直,则______.
15.直线的倾斜角是______________(用反三角函数表示).
参考答案与试题解析
1.【答案】和
【解析】当直线斜率不存在时直接得到答案,当斜率存在时设出直线斜率,写出直线方程,由点到直线的距离公式列式求出斜率,则答案可求.
【详解】
解:当直线的斜率不存在时,直线方程为;
当直线的斜率存在时,设斜率为,直线方程为,即.
由,解得.直线方程为.
故答案为:和.
【点睛】
本题考查了直线方程的求法,考查了点到直线的距离公式,关键是不要漏掉斜率不存在的情况,是基础题.
2.【答案】
【解析】由题意两条直线平行求出的值,再运用平行线之间的距离公式求出结果.
详解:由条件知两条直线:与:平行,则两条直线斜率相等,
直线:,直线:,故,,
所以直线:,即,
则两条平行线之间的距离.
故答案为:.
【点睛】
本题考查了由直线平行求参数以及求平行线之间距离,解答本题的关键是要熟记公式,并能灵活运用公式来解题,需要掌握解题方法.
3.【答案】
【解析】由直线一般式中垂直,则构建方程,解得答案.
【详解】
因为直线与直线互相垂直
所以,即.
故答案为:
【点睛】
本题考查直线垂直的应用,属于基础题.
4.【答案】-8
【解析】直线AB与直线平行,即斜率相等,由斜率公式即可得到m的值.
详解:∵直线2x+y-1=0的斜率等于﹣2,
∴过点和的直线的斜率也是﹣2,
由斜率公式得,解得m=﹣8,
故答案为:-8.
【点睛】
本题考查两条直线平行的条件,考查斜率公式,属于基础题.
5.【答案】
【解析】求出中点坐标,求出的斜率,即可得其垂直平分线斜率,从而得直线方程.
【详解】
由已知的中点为,,因此中垂线斜率为,方程为,化简得:.
故答案为:.
【点睛】
本题考查求直线方程,掌握两直线垂直的斜率关系是解题关键.
6.【答案】
【解析】根据题意,设直线的方程为,将的坐标代入计算可得的值,将其代入直线的方程,计算即可得答案.
详解:解:根据题意,直线与直线平行,设直线的方程为,
又由直线经过点,则有,解可得;
故直线的方程为,
故答案为:.
【点睛】
此题考查由两直线的位置关系求直线方程,属于基础题
7.【答案】3
【解析】由两条直线的的一个法向量恰为的一个方向向量,得出两直线垂直,然后再根据两条直线垂直,斜率乘积为,求出值.
详解:解:的一个法向量恰为的一个方向向量,
.
直线的斜率为,直线的斜率为,
由,得
.
故答案为:3.
【点睛】
本题考查斜率都存在的两条直线垂直的性质,以及直线的一般式方程与直线的垂直关系.
8.【答案】1
【解析】由两直线垂直,得到,求解,得出的值,代入直线方程检验,即可得出结果.
详解:因为直线与直线垂直,
则,即,解得:或;
因为当时,可化为,显然不成立;
当时,直线与直线显然垂直,满足题意.
故答案为:
【点睛】
本题主要考查由两直线垂直求参数,熟记两直线垂直的判定方法即可,属于常考题型.
9.【答案】
【解析】由直线和.,利用直线与直线平行的性质能求出,把转化为:,利用两平行线间的距离公式能求出两直线与间的距离.
【详解】
解:直线和,,
,解得,
∴转化为:,
两直线与间的距离是: .
故答案为:;.
【点睛】
本题考查实数值.两平行线间的距离的求法,考查直线与直线平行的性质.两平行线间距离公式等基础知识,考查运算求解能力,是基础题.
10.【答案】
【解析】先根据倾斜角确定直线的斜率,再由直线过点A,用点斜式求出直线方程。
【详解】
由题得,直线的斜率为,且直线过点,则有,整理得.
故答案为:
【点睛】
本题考查直线方程,已知直线倾斜角和它过某点,运用点斜式求直线方程。
11.【答案】
【解析】由题意,即,∴.
考点:直线的倾斜角.
12.【答案】
【解析】求出直线的斜率为,由的取值范围可知:,进而得到倾斜角的变化范围.
详解:因为直线的斜率为,
由的取值范围可知:
因此倾斜角的变化范围是:
故答案为:
【点睛】
本题考查了直线的斜率和倾斜角的关系,考查了学生转化与划归,数学运算的能力,属于中档题.
13.【答案】
【解析】首先求出与坐标轴的交点,然后再利用两点间的距离公式即可求解.
详解:令,得,令得,
即直线与两坐标轴交点分别为,,
∴,解得 .
故答案为:
【点睛】
本题考查了直线与坐标轴的交点.两点间的距离公式,考查了基本运算能力,是基础题.
14.【答案】
【解析】直接利用直线垂直公式计算得到答案.
详解:因为,所以,所以.
故答案为:
【点睛】
本题考查了根据直线垂直求参数,意在考查学生的计算能力.
15.【答案】
【解析】由方程写出斜率,根据斜率得倾斜角.
详解:直线的斜率为,
∴它的倾斜角为.
故答案为:.
【点睛】
本题考查直线的倾斜角,根据斜率与倾斜角的关系求倾斜角是常用方法.只是要注意反正切函数的值域与倾斜角的范围不相同,注意转换.
高中数学人教B版 (2019)选择性必修 第一册2.2.2 直线的方程随堂练习题: 这是一份高中数学人教B版 (2019)选择性必修 第一册2.2.2 直线的方程随堂练习题,共12页。试卷主要包含了已知,一直线过点且与轴等内容,欢迎下载使用。
高中数学人教B版 (2019)选择性必修 第一册2.2.2 直线的方程课后复习题: 这是一份高中数学人教B版 (2019)选择性必修 第一册2.2.2 直线的方程课后复习题,共11页。试卷主要包含了已知点,若直线与直线平行,则_____,已知直线等内容,欢迎下载使用。
高中数学人教B版 (2019)选择性必修 第一册2.2.2 直线的方程巩固练习: 这是一份高中数学人教B版 (2019)选择性必修 第一册2.2.2 直线的方程巩固练习,共10页。













