2022-2023学年四川省遂宁市七年级上册数学期末专项提升模拟题（AB卷）含解析

这是一份2022-2023学年四川省遂宁市七年级上册数学期末专项提升模拟题（AB卷）含解析，共40页。试卷主要包含了填 空 题，选一选，解 答 题等内容，欢迎下载使用。
2022-2023学年四川省遂宁市七年级上册数学期末专项提升模拟题（A卷）
一、填 空 题（每题2分，共24分）
1. |﹣4|=______．
2. 是____________次单项式．
3. 方程2x﹣3=0的解是__．
4. 将图中的直角三角板ABC绕AC边旋转一周得到的几何体是________．

5. 如图是一个正方体展开图，把展开图折叠成正方体后，“我”字一面的相对面上的字是_____．

6. 计算：2（x–y）+3y=__________．
7. 一张试卷只有25道选一选，答对一题得4分，答错倒扣1分，某学生解答了全部试题共得70分，他答对了__________道题．
8. 方程（2a-1）x2+3x+1=4是一元方程，则a= ______ ．
9. 一架飞机在两个城市之间飞行，顺风飞行需2.5h，逆风飞行需3h，若风速是24km/h，求两城市间距离．若飞机在无风飞行时的速度为x（km/h），根据题意，所列正确方程是___________．
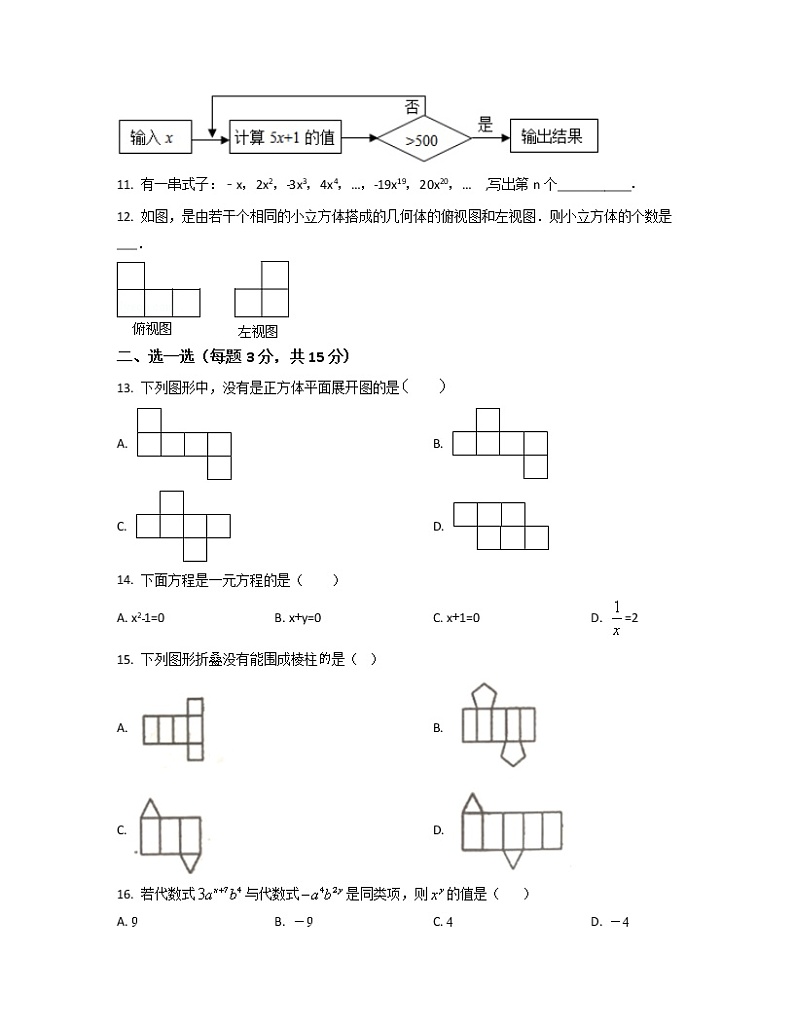
10. 按如图的程序计算，若开始输入的值x为正数，输出的结果为656，则满足条件的x的没有同值至多有_____个．

11. 有一串式子：﹣x，2x2，﹣3x3，4x4，…，﹣19x19，20x20，… ,写出第n个___________．
12. 如图，是由若干个相同的小立方体搭成的几何体的俯视图和左视图．则小立方体的个数是___．

二、选一选（每题3分，共15分）
13. 下列图形中，没有是正方体平面展开图的是　　
A. B.
C. D.
14. 下面方程是一元方程的是（　　）
A. x2﹣1=0 B. x+y=0 C. x+1=0 D. =2
15. 下列图形折叠没有能围成棱柱是（ ）
A. B.
C. D.
16. 若代数式与代数式是同类项，则的值是（ ）
A. 9 B. －9 C. 4 D. －4
17. 如果那么下列等式没有一定成立的是
A. B. C. D.
三、解 答 题
18. 计算：
（1）4+（﹣2）2×2﹣（﹣36）÷4; （2）3（2x﹣5y）﹣4（3x﹣5y）+5．
19. 解方程：(1)2（2x﹣3）﹣3=2﹣3（x﹣1） (2)．
20. 如图是由一些相同的小立方块搭成的几何体，请画出从三个没有同方向看这个几何体得到的平面图形．

（1）图中有_____块小正方体；
（2）请在下面方格纸中分别画出它的主视图，左视图和俯视图．
21. 先化简 2（x2y+3xy2）﹣3（x2y﹣1）﹣2x2y﹣2，再求值，其中x=﹣2，y=2．
22. 如果方程3(x－1)－2(x＋1)＝－3和＝1的解相同，求a的值.
23. 把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本.问这个班有多少学生？这些图书共有多少本？
24. 一个蓄水池有甲、乙两个进水管和一个丙排水管，单独开甲管6小时可注满水池；单独开乙管8小时可注满水池，单独开丙管9小时可将满池水排空，若先将甲、乙管同时开放2小时，然后打开丙管，问打开丙管后几小时可注满水池？
25. （2017四川省内江市，第26题，12分）观察下列等式：
个等式：；
第二个等式：；
第三个等式：；
第四个等式：；
按上述规律，回答下列问题：
（1）请写出第六个等式：a6= = ；
（2）用含n的代数式表示第n个等式：an= = ；
（3）a1+a2+a3+a4+a5+a6= （得出最简结果）；
（4）计算：a1+a2+…+an．
26. 平价商场经销的甲、乙两种商品，甲种商品每件售价60元，利润为20元；乙种商品每件进价50元，售价80元．
（1）甲种商品每件进价 　 　元，每件乙种商品利润率为 　 　．
（2）若该商场同时购进甲、乙两种商品共50件，恰好总进价2100元，求购进甲种商品多少件？
（3）在“元旦”期间，该商场只对甲乙两种商品进行如下优惠促销：
打折前性购物总金额
优惠措施
少于等于450元
没有优惠
超过450元但没有超过600元
按售价打九折
超过600元
其中600元部分八点二折优惠，超过600元的部分打三折优惠
按上述优惠条件，若小华性购买乙种商品实际付款504元，求小华在该商场购买乙种商品多少件？

















2022-2023学年四川省遂宁市七年级上册数学期末专项提升模拟题（A卷）
一、填 空 题（每题2分，共24分）
1. |﹣4|=______．
【正确答案】4．

【详解】解：|﹣4|=4．故答案为4．
2. 是____________次单项式．
【正确答案】3

【分析】
【详解】解：是3次单项式．
故
3. 方程2x﹣3=0的解是__．
【正确答案】

【详解】2x﹣3=0


4. 将图中的直角三角板ABC绕AC边旋转一周得到的几何体是________．

【正确答案】圆锥

【详解】将图中的直角三角板ABC绕AC边旋转一周得到的几何体是圆锥.
5. 如图是一个正方体展开图，把展开图折叠成正方体后，“我”字一面的相对面上的字是_____．

【正确答案】梦．

【分析】正方体的表面展开图，相对的面之间一定相隔一个正方形，根据这一特点作答．
【详解】解：正方体的表面展开图，相对的面之间一定相隔一个正方形，
“我”与“梦”是相对面，
“们”与“中”是相对面，
“的”与“国”是相对面．
故梦．
本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．
6. 计算：2（x–y）+3y=__________．
【正确答案】2x+y

【详解】解：原式=2x﹣2y+3y=2x+y，
故答案为2x+y.
7. 一张试卷只有25道选一选，答对一题得4分，答错倒扣1分，某学生解答了全部试题共得70分，他答对了__________道题．
【正确答案】19

【分析】设他做对了x道题，则小英做错了（25-x）道题，根据总得分=4×做对的题数-1×做错的题数，即可得出关于x的一元方程，解之即可得出结论.
【详解】解：设他做对了x道题，则他做错了（25-x）道题，
根据题意得：4x-（25-x）=70，
解得：x=19，
故答案为19.
本题考查了一元方程的应用，根据总得分=4×做对的题数-1×做错的题数列出关于x的一元方程是解题的关键.
8. 方程（2a-1）x2+3x+1=4是一元方程，则a= ______ ．
【正确答案】

【详解】由题意得2a-1=0，解得a= .
本题主要考查一元方程的概念，一元方程指只含有一个未知数、未知数的次数为1且两边都为整式的等式方程，熟练掌握一元方程的概念是解题的关键.
9. 一架飞机在两个城市之间飞行，顺风飞行需2.5h，逆风飞行需3h，若风速是24km/h，求两城市间距离．若飞机在无风飞行时的速度为x（km/h），根据题意，所列正确方程是___________．
【正确答案】2.5（x+24）=3（x﹣24）

【详解】根据来回的路程相等建立方程即可求解．
解：设飞机在无风飞行时的速度为xkm/h,可得：
2.5(x+24)=3(x-24)，
故答案为2.5(x+24)=3(x-24)
10. 按如图的程序计算，若开始输入的值x为正数，输出的结果为656，则满足条件的x的没有同值至多有_____个．

【正确答案】4

【详解】分析：根据输出的结果，可计算出它前面的那个数，依此类推，可将符合题意的那个最小的正数求出．
解：∵输出的数为656，
∴5x+1=656，得：x=131＞0，
5x+1=131，得：x=26＞0，
5x+1=26，得：x=5＞0，
5x+1=5，得：x=0.8＞0；
5x+1=0.8，得：x=-0.04＜0，没有符合题意，
故x的值可取131，26，5，0.8共4个．
故答案为4．
11. 有一串式子：﹣x，2x2，﹣3x3，4x4，…，﹣19x19，20x20，… ,写出第n个___________．
【正确答案】（﹣1）nnxn

【详解】排列规律是：每一项的系数正负相间，奇数项的系数为负，偶数项的系数为正，系数的值等于项数.字母部分是x的幂，其指数等于项数.
用代数式表示为：第n项是(-1)n·nxn（n为正整数）.
故答案为（﹣1）nnxn.
12. 如图，是由若干个相同小立方体搭成的几何体的俯视图和左视图．则小立方体的个数是___．

【正确答案】5或6或7

【详解】解：由俯视图易得层有4个立方体，由左视图易得第二层至多有3个立方体和至少有1个立方体，
那么小立方体的个数可能是5个或6个或7个.
故答案为5或6或7.
二、选一选（每题3分，共15分）
13. 下列图形中，没有是正方体平面展开图的是　　
A. B.
C. D.
【正确答案】D

【分析】由平面图形的折叠及正方体的展开图解题．
【详解】解：由四棱柱四个侧面和上下两个底面的特征可知，
A，B，C选项可以拼成一个正方体；
而D选项，上底面没有可能有两个，故没有是正方体的展开图．
故选D．
本题考查四棱柱的特征及正方体展开图的各种情形，难度适中．
14. 下面方程是一元方程的是（　　）
A. x2﹣1=0 B. x+y=0 C. x+1=0 D. =2
【正确答案】C

【详解】根据只含有一个未知数（元），且未知数的次数是1，这样的方程叫一元方程进行分析即可．
解：A. 没有是一元方程，故此选项错误；
B. 没有是一元方程，故此选项错误；
C. 是一元方程，故此选项正确；
D. 没有是一元方程，故此选项错误；
故选C.
15. 下列图形折叠没有能围成棱柱的是（ ）
A. B.
C. D.
【正确答案】D

【分析】根据平面图形的折叠及棱柱的展开图的特点排除即可．
【详解】解：A选项可以围成四棱柱；
B选项可以围成五棱柱；
C选项可以围成三棱柱；
D选项侧面上多出2个长方形，故没有能围成一个三棱柱．
故答案为D．
本题考查了立体图形的展开与折叠，掌握常见立体图形的表面展开图的特征是解这类题的关键．
16. 若代数式与代数式是同类项，则的值是（ ）
A. 9 B. －9 C. 4 D. －4
【正确答案】A

【分析】根据同类项的定义（所含字母相同，相同字母的指数相同）列出方程x+7＝4，2y＝4，求出x，y的值，再代入代数式计算即可．
【详解】解：∵代数式3ax+7b4与代数式﹣a4b2y是同类项，
∴x+7＝4，2y＝4，
∴x＝﹣3，y＝2；
∴xy＝（﹣3）2＝9．
故选：A．
本题考查了同类项的定义．注意同类项定义中的两个“相同”：（1）所含字母相同；（2）相同字母的指数相同，是易混点，因此成了中考的常考点．解题时注意运用二元方程组求字母的值．
17. 如果那么下列等式没有一定成立的是
A. B. C. D.
【正确答案】D

【详解】试题解析：A. 等式x=y的两边同时加上a，该等式仍然成立；故本选项正确；
B. 等式x=y的两边同时减去a，该等式仍然成立；故本选项正确；
C. 等式x=y的两边同时乘以a，该等式仍然成立；故本选项正确；
D 当a=0时， 无意义；故本选项错误；
故选D.
三、解 答 题
18. 计算：
（1）4+（﹣2）2×2﹣（﹣36）÷4; （2）3（2x﹣5y）﹣4（3x﹣5y）+5．
【正确答案】（1）21；（2）﹣6x+5y+5．

【详解】（1）按有理数混合运算顺序：先乘方，再乘除，加减进行计算即可；
（2）先去括号，再合并同类项即可.
解：（1）原式＝4+4×2+9＝4+8+9＝21；
（2）原式＝6x-15y-12x+20y+5=﹣6x+5y+5．
19. 解方程：(1)2（2x﹣3）﹣3=2﹣3（x﹣1） (2)．
【正确答案】（1）x=2（2）x=3

【详解】按解一元方程一般步骤解方程即可.
解：（1）去括号，得4x-6-3=2-3x+3,
移项，得4x+3x=2+3+6+3,
合并同类项得，7x=14,
系数化为1得，x=2；
（2）去分母得，2(x-3)-6=3(-2x+4),
去括号，得2x-6-6=-6x+12,
移项，得2x+6x=12+6+6,
合并同类项得，8x=24,
系数化为1得，x=3.
20. 如图是由一些相同的小立方块搭成的几何体，请画出从三个没有同方向看这个几何体得到的平面图形．

（1）图中有_____块小正方体；
（2）请在下面方格纸中分别画出它的主视图，左视图和俯视图．
【正确答案】6

【详解】（1）根据实物图形直接得出图形组成个数即可；
（2）主视图有3列，每列小正方形数目分别为1，2，1；左视图有3列，每列小正方形数目分别为1，2，1；俯视图有3行，每行小正方形数目分别为1，3，1．
解：（1）6；
（2）根据实物图可以画出图形的三视图．

21. 先化简 2（x2y+3xy2）﹣3（x2y﹣1）﹣2x2y﹣2，再求值，其中x=﹣2，y=2．
【正确答案】﹣71．

【详解】先去括号，再合并同类项，代入求值即可.
解：原式=2x2y+6xy2﹣3x2y+3﹣2x2y﹣2
=﹣3x2y+6xy2+1，
当x=﹣2，y=2时，原式=﹣24﹣48+1=﹣71．
22. 如果方程3(x－1)－2(x＋1)＝－3和＝1的解相同，求a的值.
【正确答案】a=-2

【详解】先解第1个方程得出x的值，再代入第2个方程中，将第2个方程转化为关于a的方程，解方程即可得出a的值.
解：方程3（x﹣1）﹣2（x+1）=﹣3，
去括号得：3x﹣3﹣2x﹣2=﹣3，
解得：x=2，
把x=2代入方程=1得：1﹣=1，
解得：a=﹣2．
23. 把一些图书分给某班学生阅读，如果每人分3本，则剩余20本；如果每人分4本，则还缺25本.问这个班有多少学生？这些图书共有多少本？
【正确答案】见解析

【详解】设这个班有x个学生
3x+20=4x-25
x=45
图书：3x+20=3×45+20=155(本)
答这个班有45名学生，图书有155本.
24. 一个蓄水池有甲、乙两个进水管和一个丙排水管，单独开甲管6小时可注满水池；单独开乙管8小时可注满水池，单独开丙管9小时可将满池水排空，若先将甲、乙管同时开放2小时，然后打开丙管，问打开丙管后几小时可注满水池？
【正确答案】打开丙管后小时可注满水池．

【详解】设打开丙管后x小时可注满水池．等量关系为：甲注水量+乙注水量-丙排水量=1． 据此列出方程并解答．
解：设打开丙管后x小时可注满水池，
由题意得，（+）（x+2）﹣x =1，
解这个方程，（x+2）﹣=1，
21x+42﹣8x=72，
13x=30，
解得x=．
答：打开丙管后小时可注满水池．
25. （2017四川省内江市，第26题，12分）观察下列等式：
个等式：；
第二个等式：；
第三个等式：；
第四个等式：；
按上述规律，回答下列问题：
（1）请写出第六个等式：a6= = ；
（2）用含n的代数式表示第n个等式：an= = ；
（3）a1+a2+a3+a4+a5+a6= （得出最简结果）；
（4）计算：a1+a2+…+an．
【正确答案】（1），；（2），；（3）；（4）．

【详解】试题分析：（1）根据已知4个等式可得；
（2）根据已知等式得出答案；
（3）利用所得等式的规律列出算式，然后两两相消，计算化简后的算式即可得；
（4）根据已知等式规律，列项相消求解可得．
试题解析：（1）由题意知，a6= =，
故答案为，；
（2）an= =，
故答案为，；
（3）原式= ==，
故答案为；
（4）原式===．
26. 平价商场经销的甲、乙两种商品，甲种商品每件售价60元，利润为20元；乙种商品每件进价50元，售价80元．
（1）甲种商品每件进价为 　 　元，每件乙种商品利润率为 　 　．
（2）若该商场同时购进甲、乙两种商品共50件，恰好总进价为2100元，求购进甲种商品多少件？
（3）在“元旦”期间，该商场只对甲乙两种商品进行如下的优惠促销：
打折前性购物总金额
优惠措施
少于等于450元
没有优惠
超过450元但没有超过600元
按售价打九折
超过600元
其中600元部分八点二折优惠，超过600元的部分打三折优惠
按上述优惠条件，若小华性购买乙种商品实际付款504元，求小华该商场购买乙种商品多少件？
【正确答案】（1）40， ；（2）40；（3）7件或8件

【分析】（1）利用售价减去利润，可得甲种商品每件进价；利用利润除以进价，可得每件乙种商品利润率，即可求解；
（2）设购进甲种商品 件，则购进乙种商品 件，根据“购进甲、乙两种商品共50件，恰好总进价为2100元”列出方程，即可求解；
（3）设小华打折前应付款为y元，然后根据打折前购物金额超过450元，但没有超过600元和打折前购物金额超过600元两种情况分别计算，即可求解．
【详解】解：（1）甲种商品每件进价为 元，
每件乙种商品利润率为 ；
（2）设购进甲种商品 件，则购进乙种商品 件，根据题意得：
，
解得： ，
答：购进甲种商品40件；
（3）设小华打折前应付款为y元，
①打折前购物金额超过450元，但没有超过600元，由题意得：
0.9y= 504，
解得：y= 560，
560 ÷ 80 = 7（件），
②打折前购物金额超过600元，
600 × 0.82 +（y-600）× 0.3= 504，
解得：y= 640，
640÷80=8（件），
综上可得：小华在该商场购买乙种商品件7件或8件．
本题主要考查了一元方程的应用，明确题意，准确得到等量关系是解题的关键．


























2022-2023学年四川省遂宁市七年级上册数学期末专项提升模拟题（B卷）
一、选一选：（本大题共有10小题，每小题3份，共30分，以下各题都有四个选项，其中只有一个选项是正确的，选出正确答案，并在答题卡上将该项涂黑.）
1. 下列算式中，运算结果是负数的是（ ）
A. –（–3） B. –32 C. |–3| D. （–3）2
2. “嫦娥一号”卫星顺利进入绕月工作轨道，行程约有1800000千米，1800000这个数用科学记数法可以表示为
A. B. C. D.
3. 下列各数：3.14，﹣2，0.1010010001…，0，﹣π，，0.，其中无理数有（　　）
A. 1个 B. 2个 C. 3个 D. 4个
4. 下列图形中，没有能折叠成一个正方体的是（）
A. B.
C. D.
5. 如图，将一张长方形纸片ABCD沿EF折叠，点A、B分别落在点A’B’处，若，则的度数是（）

A. B. C. D.
6. 下列说法错误的是（）
A. 两点之间线段最短 B. 同一平面内，过一点有且只有一条直线与已知直线垂直
C. 同角的余角相等 D. 过一点有且只有一条直线与已知直线平行
7. 一件毛衣先按成本提高50%标价，再以8折出售，获利28元，求这件毛衣的成本是多少元，若设成本是x元，可列方程为（　　）
A. 0.8x+28=（1+50%）x B. 0.8x﹣28=（1+50%）x C. x+28=0.8×（1+50%）x D. x﹣28=0.8×（1+50%）x
8. 如图，OA⊥OB，∠BOC=50°，OD平分∠AOC，则∠BOD度数是（　　）

A. 20o B. 30o C. 40o D. 50o
9. 将一副三角板按如图方式摆放，∠1与∠2没有一定互补的是（ ）
A. B. C. D.
10. 在一列数:中， 从第三个数开始，每一个数都等于它前两个数之积的个位数字，则这个数中的第2018个数是（）
A. 1 B. 3 C. 7 D. 9
二、填 空 题：（本大题共8小题，每小题3分，共24分，把答案直接填在答题卡相应的位置上）
11. 的倒数是________.
12. 如图所示的三角形绕边AB所在直线旋转一周所形成的几何体是_____．

13. 若5x2y和－xmyn是同类项，则2m－5n＝__________．
14. 如图，船A在灯塔O的正东方向，船B在灯塔O的北偏东处，则的度数是______.

15. 若关于x的方程与的解相同，则这两个方程的解为x = _____.
16. 已知，则的值是_________.
17. 如图，有理数在数轴上，则化简结果是_______.

18. 已知点C是线段AB的中点，点D在直线AB上，BD=AB，若AD=16，则CD=_________.
三、解 答 题：（本大题共10小题，共76分，把解答过程写在答题卡相应的位置上，解答时应写出必要的计算过程、推演步骤或文字说明.）
19. 计算：
（1）；
（2）.
20. 解方程：
（1）；
（2） .
21. 先化简，再求值：，其中．
22. 如图，在的正方形网格中，点P是的边OB上的一点．
（1）过点P画OB的垂线，交OA于点C；过点P画OA的垂线，垂足为H；
（2）线段PH的长度是点P到直线__________的距离；
（3）线段__________长度是点C到直线OB的距离；
（4）线段PC、PH、OC这三条线段大小关系是__________（用“1时，是正数；当原数的值