2022-2023学年北京市东城区七年级下册数学期末专项提升模拟题（AB卷）含解析

这是一份2022-2023学年北京市东城区七年级下册数学期末专项提升模拟题（AB卷）含解析，共44页。试卷主要包含了选一选，填 空 题，解 答 题等内容，欢迎下载使用。
2022-2023学年北京市东城区七年级下册数学期末专项提升模拟题（A卷）
一、选一选（本大题共 10 小题，每小题 3 分，共 30 分.在每小题给出的四个选 项中，只有一项是符合题目要求的，把答案填在答题卷中）
1. 下列运算正确的是（ ）
A. a4 + a5 = a9 B. a4· a2 = a8 C. a3¸ a3= 0 D. (-a2 )3=-a6
2. 下列各式中，相等关系一定成立的是（）
A. (x + 6)(x − 6) = x 2 − 6 B. (x − y)2 = (y − x)2
C. (x− 2)(x − 6) = x 2 – 2x – 6x − 12 D. (x + y)2 = x 2 + y2
3. 变量x与y之间的关系式y＝x2﹣2，当自变量x＝2时，因变量y的值是（　　）．
A ﹣2 B. ﹣1 C. 0 D. 1
4. 下列中，是必然的是（　　）
A. 打开电视，它正在播广告
B. 抛掷一枚硬币，正面朝上
C. 打雷后会下雨
D. 367人中有至少两人的生日相同
5. 下列正确说法的个数是 （ ）
①同位角相等 ②对顶角相等
③等角的补角相等 ④两直线平行，同旁内角相等
A. 1 B. 2 C. 3 D. 4
6. 如图，用尺规作一个角等于已知角，其作图原理是：由△ODC≌△O′D′C′得∠AOB＝∠A′O′B′，其依据的定理是（　　）

A. SSS B. SAS C. ASA D. AAS
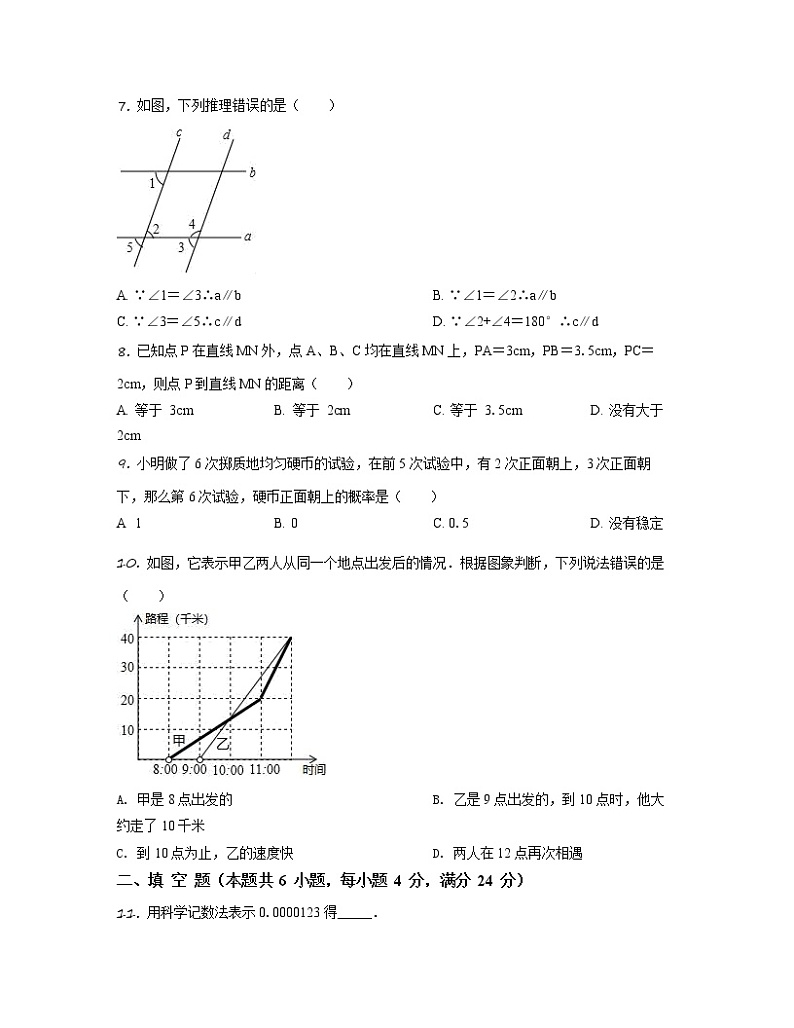
7. 如图，下列推理错误的是（　　）

A. ∵∠1＝∠3∴a∥b B. ∵∠1＝∠2∴a∥b
C. ∵∠3＝∠5∴c∥d D. ∵∠2+∠4＝180°∴c∥d
8. 已知点P在直线MN外，点A、B、C均在直线MN上，PA＝3cm，PB＝3.5cm，PC＝2cm，则点P到直线MN的距离（　　）
A. 等于 3cm B. 等于 2cm C. 等于 3.5cm D. 没有大于 2cm
9. 小明做了6次掷质地均匀硬币的试验，在前5次试验中，有2次正面朝上，3次正面朝下，那么第6次试验，硬币正面朝上的概率是（　　）
A 1 B. 0 C. 0.5 D. 没有稳定
10. 如图，它表示甲乙两人从同一个地点出发后的情况．根据图象判断，下列说法错误的是（　　）

A. 甲是8点出发的 B. 乙是9点出发的，到10点时，他大约走了10千米
C. 到10点为止，乙的速度快 D. 两人在12点再次相遇
二、填 空 题（本题共 6 小题，每小题 4 分，满分 24 分）
11. 用科学记数法表示0.0000123得_____．
12. 在直角三角形中，一个锐角比另外一个锐角的3倍还多10°，则这两个角分别为_____
13. 等腰三角形顶角和一个底角的度数的比是4：1，则底角的度数为_____．
14. 已知△ABC中，AB＝2，BC＝5，且AC的长为偶数，则AC的长为_____．
15. 计算：（x3﹣2x）÷（x）＝_____．
16. 如果将（a + b）n （n 为非负整数）的每一项按字母 a 的次数由大到小排列，可以得到下 面的等式（1），然后将每个式子的各项系数排列成（2）：
(a + b)1 = a + b 1 1
（a + b）2 = a2 + 2ab + b2 1 2 1
（a + b）3 = a3 + 3a2b + 3ab2 + b3 1 3 3 1
（a + b）4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 1 4 6 4 1
根据规律可得：（a + b）5=（_____________________）
三、解 答 题
17. 计算：
18. 如图，已知AB∥DC，AB＝DC，则AD∥BC吗？说明理由．

19. 如图，假设可以随机在图中取点．

（1）这个点取在阴影部分的概率是　 　．
（2）在保留原阴影部分情况下，请你重新设计图案（直接在图上涂阴影），使得这个点取在阴影部分的概率为．
20. 先化简，再求值：，其中．
21. 图a是一个长为2m、宽为2n的长方形，沿图中实现用剪刀均分成四块小长方形，然后按图b的形状拼成一个正方形．

（1）图b中，大正方形的边长是　 　．阴影部分小正方形的边长是　 　；
（2）观察图b，写出（m+n）2，（m﹣n）2，mn之间的一个等量关系，并说明理由．
22. 如图，△ABC中

（1）尺规作图：作AB的垂直平分线DE，交AC于点D，交AB于点 E．
（2）在（1）图中连DB，如果AC＝10，BC＝6，求△DBC的周长．
23. 已知某弹簧长度的挂重为25千克，在弹性限度内，用x表示的物体的质量，用y表示弹簧的长度，其关系如表：
所挂物体质量的质量/千克
0
1
2
3
4
5
6
7
8
弹簧的长度/cm
12
12.5
13
13.5
14
14.5
15
15.5
16
（1）弹簧没有挂物体时的长度是　 　cm；
（2）随着x的变化，y的变化趋势是：　 　；
（3）根据表中数据的变化关系，写出y与x的关系式，并指出自变量的取值范围是　 　．
24. 如图，在四边形ABCD中，AD∥BC，E为CD中点，连接AE、BE，延长AE交BC的延长线于点F．

（1）△DAE和△CFE全等吗？说明理由；
（2）若AB＝BC+AD，说明BE⊥AF；
（3）在（2）的条件下，若EF＝6，CE＝5，∠D＝90°，你能否求出E到AB的距离？如果能请直接写出结果．
25. 如图，已知△ABC 中，AB=AC=6cm，∠B=∠C，BC=4cm，点 D 为 AB的中点．
（1）如果点 P 在线段 BC 上以 1cm/s 速度由点 B 向点 C 运动，同时，点 Q 在线段 CA 上由点 C 向点 A 运动．
①若点 Q 的运动速度与点 P 的运动速度相等， 1 秒后，△BPD 与△CQP 是否全等，请说明理由；
②若点 Q 的运动速度与点 P 的运动速度没有相等，当点 Q 的运动速度为多少时，能够使△BPD 与△CQP 全等？
（2）若点 Q 以②中的运动速度从点 C 出发，点 P 以原来的运动速度从点 B 同时出发，都逆时针沿△ABC 三边运动，则 后，点 P 与点 Q 次在△ABC 的 边上相遇？（在横线上直接写出答案，没有必书写解题过程）




2022-2023学年北京市东城区七年级下册数学期末专项提升模拟题（A卷）
一、选一选（本大题共 10 小题，每小题 3 分，共 30 分.在每小题给出的四个选 项中，只有一项是符合题目要求的，把答案填在答题卷中）
1. 下列运算正确的是（ ）
A. a4 + a5 = a9 B. a4· a2 = a8 C. a3¸ a3= 0 D. (-a2 )3=-a6
【正确答案】D

【详解】分析：根据合并同类项、同底数幂的乘法、同底数幂的除法、幂的乘方逐项计算即可.
详解：A. ∵ a4 与 a5 没有是同类项，没有能合并，故错误；
B. ∵ a4·a2 = a6 ，故错误；
C. a3¸ a3= 1 ，故错误；
D. (-a2 )3=-a6，故正确；
故选D.
点睛：本题考查了整式的运算，熟练掌握合并同类项、同底数幂的乘法、同底数幂的除法、幂的乘方的运算法则是解答本题的关键.
2. 下列各式中，相等关系一定成立的是（）
A. (x + 6)(x − 6) = x 2 − 6 B. (x − y)2 = (y − x)2
C. (x− 2)(x − 6) = x 2 – 2x – 6x − 12 D. (x + y)2 = x 2 + y2
【正确答案】B

【详解】分析：根据平方差公式、偶次方的性质、多项式乘多项式、完全平方公式逐项分析即可.
详解：A. ∵(x + 6)(x − 6) = x 2 – 36，故没有成立；
B. ∵ (x − y)2 = (y − x)2，故成立；
C. ∵(x− 2)(x − 6) = x 2 – 2x – 6x + 12，故没有成立；
D. (x + y)2 = x 2 +2xy+ y2，故没有成立；
故选B.
点睛：本题考查了多项式的乘法，熟练掌握平方差公式、偶次方的性质、多项式乘多项式、完全平方公式是解答本题的关键.
3. 变量x与y之间的关系式y＝x2﹣2，当自变量x＝2时，因变量y的值是（　　）．
A. ﹣2 B. ﹣1 C. 0 D. 1
【正确答案】C

【分析】把自变量x的值代入函数解析式进行计算即可得解．
【详解】解：x=2时，y=×2 2 – 2=0．
故选C．
本题考查了函数值的求解，是基础题，准确计算是解题的关键．
4. 下列中，是必然的是（　　）
A. 打开电视，它正在播广告
B. 抛掷一枚硬币，正面朝上
C. 打雷后会下雨
D. 367人中有至少两人的生日相同
【正确答案】D

【详解】分析：必然指在一定条件下一定发生的，据此解答即可.
详解：A. 打开电视，它正在播广告是随机；
B. 抛掷一枚硬币，正面朝上随机；
C. 打雷后下雨是随机；
D. ∵一年有365天，∴ 367 人中有至少两个人的生日相同是必然.
故选D.
点睛：本题考查了必然的定义，解决本题需要正确理解必然、没有可能、随机的概念．必然指在一定条件下一定发生的．没有可能是指在一定条件下，一定没有发生的．没有确定即随机是指在一定条件下，可能发生也可能没有发生的．
5. 下列正确说法的个数是 （ ）
①同位角相等 ②对顶角相等
③等角的补角相等 ④两直线平行，同旁内角相等
A. 1 B. 2 C. 3 D. 4
【正确答案】B

【详解】分析：由平行线的性质定理,对顶角相等以及等角的补角相等的性质,即可求得答案.
详解：∵两直线平行,同位角相等;故①错误;
∵对顶角相等,故②正确;
∵等角补角相等,故③正确;
∵两直线平行,同旁内角互补,故④错误.
∴其中正确的有②③共2个.
故选B.
点睛：题考查了平行线的性质定理、对顶角相等、等角的补角相等的知识.解此题的关键是熟记定理.
6. 如图，用尺规作一个角等于已知角，其作图原理是：由△ODC≌△O′D′C′得∠AOB＝∠A′O′B′，其依据的定理是（　　）

A. SSS B. SAS C. ASA D. AAS
【正确答案】A

【详解】分析：在做一个角等于已知角时，实际上作的是三边对应相等，根据三边对应相等两三角形全等，全等三角形的对应角相等可知所作的角等于已知角.
详解：在△OCD与△O′C′D′，
∵ ,
∴△OCD≌△O′C′D′（SSS），
∴∠A′O′B′=∠AOB，
显然运用的判定方法是SSS．
故选A.
点睛：本题考点是全等三角形的判定和性质的应用，熟练掌握全等三角形的判定和性质定理是解决本题的关键，本题是常考题，要熟练掌握
7. 如图，下列推理错误的是（　　）

A. ∵∠1＝∠3∴a∥b B. ∵∠1＝∠2∴a∥b
C. ∵∠3＝∠5∴c∥d D. ∵∠2+∠4＝180°∴c∥d
【正确答案】A

【详解】分析：根据平行线的判定方法逐项分析即可.
详解：A. ∵∠1与∠3没有具有位置关系，∴没有能推出a∥b ；
B. ∵∠1与∠2是一对内错角，∴由∠1=∠2能推出a∥b；
C. ∵∠3与∠5是一对同位角，∴由∠3=∠5能推出c∥d；
D. ∵∠2与∠4是一对同旁内角，∴由∠2+∠4=180°能推出c∥d.
故选A.
点睛：本题考查了平行线的判定方法：①两同位角相等，两直线平行； ②内错角相等，两直线平行；③同旁内角互补，两直线平行；④平行于同一直线的两条直线互相平行；同一平面内，垂直于同一直线的两条直线互相平行.
8. 已知点P在直线MN外，点A、B、C均在直线MN上，PA＝3cm，PB＝3.5cm，PC＝2cm，则点P到直线MN的距离（　　）
A. 等于 3cm B. 等于 2cm C. 等于 3.5cm D. 没有大于 2cm
【正确答案】D

【详解】分析：根据垂线段最短得出点P到直线MN的距离小于或等于2cm，即可得出答案．
详解：∵垂线段最短，
又∵点P在直线MN外，点A、B、C均在直线MN上，PA=3cm，PB=3.5cm，PC=2cm，
∴点P到直线MN的距离小于或等于2cm，即没有大于2cm，
故选D．
点睛：本题考查了点到直线的距离和垂线段最短的应用，注意：从直线外一点到这条直线的垂线段的长度叫点到直线的距离．
9. 小明做了6次掷质地均匀硬币的试验，在前5次试验中，有2次正面朝上，3次正面朝下，那么第6次试验，硬币正面朝上的概率是（　　）
A. 1 B. 0 C. 0.5 D. 没有稳定
【正确答案】C

【详解】分析：本题是一道列举法求概率的问题，属于基础题，可以直接用概率的公式求解．
详解：因为一枚质地均匀的硬币只有正反两面，所以没有管抛多少次，硬币正面朝上的概率都是.
故选C. 
点睛：本题考查了概率的意义，一般地，在大量重复实验中，如果A发生的频率 会稳定在某个常数p附近，那么这个常数p就叫做A的概率，记为P( A) =p．明确概率的意义是解答的关键，用到的知识点为：概率=所求情况数与总情况数之比．
10. 如图，它表示甲乙两人从同一个地点出发后的情况．根据图象判断，下列说法错误的是（　　）

A. 甲是8点出发的 B. 乙是9点出发的，到10点时，他大约走了10千米
C. 到10点为止，乙的速度快 D. 两人在12点再次相遇
【正确答案】B

【详解】分析：从图象可知:甲做变速运动,8时到11时走了20千米,速度为每小时千米,11时到12时走了20千米,速度为每小时20千米;乙做的是匀速运动,9时到12时走了40千米,速度是每小时千米.
详解：A.由图像知，甲8点出发，故A正确;
B. 由图像知，乙9点出发;到10时他大约走了13千米，故B没有正确;
C.到10时为止, 甲的速度为每小时千米, 乙的速度是每小时千米，乙的速度快，故C正确;
D. 由图像知，两人最终在12时相遇，故D正确.
故选B.
点睛：本题考查了函数的图象,图中反映的是甲乙两人行驶的路程与时间之间的关系,甲的速度有变化,乙是匀速运动的.
二、填 空 题（本题共 6 小题，每小题 4 分，满分 24 分）
11. 用科学记数法表示0.0000123得_____．
【正确答案】

【分析】对于一个值小于1的非0小数，用科学记数法写成 的形式，其中，n是正整数，n等于原数中个非0数字前面所有0的个数（包括小数点前面的0）.
【详解】解：0.0000123=1.23×10-5
故答案为1.23×10－5.
本题考查了负整数指数科学记数法, 根据科学计算法的要求，正确确定出a和n的值是解答本题的关键.
12. 在直角三角形中，一个锐角比另外一个锐角的3倍还多10°，则这两个角分别为_____
【正确答案】20°，70°

【详解】分析：因为直角三角形的两个锐角的和是90度，所以设其中一个锐角的度数是x度，则另一个锐角的度数就是3x+10度，据此即可列方程求解．
详解：设其中一个锐角的度数是x度，则另一个锐角的度数就是3x+10度，
由题意得，
x+3x+10=90
 4x=80
x=20
3x+10
=3×20+10
=70
∴这两个角分别为20°，70°.
故答案为20，70°.
点睛：此题主要是考查了直角三角形的两个锐角互余，还用到了一元方程的知识，解答此题的关键是找准对应量，找出数量关系，根据数量关系列方程解答．
13. 等腰三角形的顶角和一个底角的度数的比是4：1，则底角的度数为_____．
【正确答案】30°

【详解】分析：根据等腰三角形两底角相等,利用三角形的内角和等于180°列式计算即可得解.
详解：∵等腰三角形的顶角和它的一个底角的度数比是4:1，
∴它的底角为
故30°.
点睛：本题考查了等腰三角形的性质,三角形的内角和定理,熟记等腰三角形两底角相等是解题的关键.
14. 已知△ABC中，AB＝2，BC＝5，且AC的长为偶数，则AC的长为_____．
【正确答案】4 或 6

【详解】分析：先根据三角形三条边的关系求出AC的取值范围，然后找出其中的偶数即可.
详解：∵AB=2，BC=5，
∴30，
因此点B在象限．
故选：A．
4. 在以下实数，，1.414，1.010010001…，42，，，中，无理数有（　　）
A. 2个 B. 3个 C. 4个 D. 5个
【正确答案】B

【详解】分析：无理数指无限没有循环小数，本题根据定义即可得出答案．
详解：本题中无理数有：1.010010001…，，，共3个，故选B．
点睛：本题主要考查的就是无理数的定义，属于基础题型．初中阶段主要有以下几种形式：(1)、构造的数，如0.12122122212222...（相邻两个1之间依次多一个2）等；(2)、有意义的数，如圆周率π等；(3)、部分带根号的数，如，等．
5. 下列说法：①对顶角相等；②在同一平面内，垂直于同一条直线的两直线平行；③相等的角是对顶角；④内错角相等．其中错误的有(　　)
A. ①② B. ①③ C. ②④ D. ③④
【正确答案】D

【详解】试题解析：①对顶角相等，正确，是真命题；
②在同一平面内，垂直于同一条直线的两直线平行，正确，是真命题；
③相等的角是对顶角，错误，是假命题；
④同位角相等，错误，是假命题.
故选D.
6. 下列各式正确的是（ ）
A. B. C. D.
【正确答案】A

【详解】【分析】根据算术平方根、立方根的定义逐一进行判断即可得.
【详解】A. ，故A选项正确；
B. ，故B选项错误；
C. ，，故C选项错误；
D. 无意义，故D选项错误，
故选A.
本题考查了利用算术平方根、立方根的定义进行化简，熟知负数没有算术平方根以及算术平方根、立方根的定义是解题的关键.
7. 若点在第三象限，且点到轴的距离为，到轴的距离为，则点的坐标是（ ）
A. B. C. D.
【正确答案】A

【分析】根据第三象限内点的横坐标与纵坐标都是负数，点到轴的距离等于纵坐标的值，到轴的距离等于横坐标的值解答．
【详解】解：点在第三象限，且点到轴的距离为3，到轴的距离为2，
，，
点的坐标是．
故选：A．
本题考查了点的坐标，解题的关键是熟记点到轴的距离等于纵坐标的值，到轴的距离等于横坐标的值．
8. 如图，BDAC，BE平分∠ABD，交AC于点E，若∠A=50°，则∠1的度数为（ ）

A. 65° B. 60° C. 55° D. 50°
【正确答案】A

【详解】解：∵BDAC，∠A=50°，
∴∠ABD=130°，
又∵BE平分∠ABD，
∴∠1=∠ABD=65°，
故选A．
9. 如果点P(-2，4)经平移变换后是Q(3，-2)，则点M(1，-2)经这样平移后的对应点的坐标是（ ）
A. (5，3) B. (-4，4) C. (6，-8) D. (3，-5)
【正确答案】C

【详解】【分析】先由P与Q的坐标得出对应点之间的关系是横坐标加5，纵坐标减6，那么让点M的横坐标加5，纵坐标减6即可得所求点的坐标．
【详解】∵点P（-2，4）经平移变换后是Q（3，-2），
∴可知是先向右平移5个单位长度，再向下平移6个单位长度，即横坐标加5，纵坐标减6可得对应点的坐标，
∴点M（1，-2）经这样平移后的对应点的坐标是（1+5，-2-6），即（6，-8），
故选C．
本题考查点的平移，解决本题的关键是根据已知对应点找到各对应点之间的变化规律．
10. 如图，把一张长方形纸片沿折叠后，点、分别落在点D′、C′的位置．若，则∠AED′的大小是（ ）

A. B. C. D.
【正确答案】C

【分析】先根据长方形的性质得出的度数，再根据翻折变换的性质得出∠D′EF的度数，根据平角的定义即可得出结论．
【详解】解：∵四边形ABCD是长方形，
∴AD//BC，
∴，
∵长方形纸片沿折叠后，点、分别落在点D′、C′的位置，
∴=∠D′EF，
∴∠D′EF=65°，
∴∠AED′=180°-2×65°=50°．
故选C.
本题考查的是长方形的性质以及折叠的性质，用到的知识点为：两直线平行，内错角相等．
二、填 空 题（本大题共8道小题，每小题3分，共24分）
11. 的平方根是______________ ；=_______________
【正确答案】 ①. ±2 ②.

【详解】分析：(1)、一个正数的平方根有两个，他们互为相反数；(2)、负数的值等于它的相反数．
详解：(1)、∵，， ∴的平方根为±2；
(2)、∵， ∴
点睛：本题主要考查的就是平方根的计算以及值的计算，属于基础题型．非负数的平方根有两个，他们互为相反数；正数的值等于它本身，负数的值等于它的相反数，零的值为零．
12. 将“对顶角相等”改写为“如果．．．那么．．．”的形式，可写为__________．
【正确答案】如果两个角互为对顶角，那么这两个角相等

【分析】根据命题的形式解答即可．
【详解】将“对顶角相等”改写为“如果．．．那么．．．”的形式，可写为如果两个角互为对顶角，那么这两个角相等，
故如果两个角互为对顶角，那么这两个角相等．
此题考查命题的形式，可写成用关联词“如果．．．那么．．．”连接的形式，准确确定命题中的题设和结论是解题的关键．
13. 若点A（2，n）在x轴上，则点B（n﹣1，n+1）在_____象限．
【正确答案】第二

【分析】先根据x轴上点的纵坐标等于零，可得n的值，再根据第二象限的横坐标小于零，纵坐标大于零，可得答案.
【详解】由点在x轴上得：
则点的坐标为

点在第二象限
即点在第二象限
故第二.
本题考查了平面直角坐标系的象限特点，象限符号规律为：象限、第二象限、第三象限、第四象限，根据题意求出n的值是解题关键.
14. 若，，则__________________.
【正确答案】1.01

【详解】【分析】由于1.0201比102.01小数点向左移动了二位，那么则它的平方根就向左移动一位，根据此规律即可解题．
【详解】∵，
∴1.01，
故答案为1.01.
本题主要考查了平方根的定义，解题关键是小数点的位置，要会从条件中找到规律：所求数的小数点向左移动了二位，则它的平方根就向左移动一位．
15. 如图所示，要把河中水引到水池A中，应在河岸B处（AB⊥CD）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是_____．

【正确答案】垂线段最短

【分析】根据垂线段的性质，可得答案．
【详解】解：要把河中的水引到水池A中，应在河岸B处（AB⊥CD）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是垂线段最短，
故垂线段最短．
本题考查了垂线段最短，利用了垂线段的性质：直线外的点与直线上所有点的连线：垂线段最短．
16. 若+（b+4）2=0，则点M（a，b）关于y轴的对称点的坐标为______
【正确答案】（-3，-4）

【分析】先根据非负数的性质求出a、b的值，然后再根据关于y轴对称的两个点的横坐标互为相反数，纵坐标没有变即可得.
【详解】∵+（b+4）2=0，
∴a-3=0，b+4=0，
∴a=3，b=-4，
∴M（a，b）为M（3，-4），
∴点M（a，b）关于y轴的对称点的坐标为（-3，-4），
故（-3，-4）.
本题考查了非负数的性质、关于y轴对称的点的坐标，解题的关键是根据几个非负数的和为0，那么每个非负数都为0求出a、b的值.
17. 如图，直线AB，CD相交于点O，OE⊥AB，∠COE＝68°，则∠BOD度数为________．

【正确答案】22°

【详解】∵OE⊥AB，
∴∠AOE=90°；
又∵∠COE=68°，
∴∠AOC=∠AOE-∠COE=22°，
∴∠BOD=∠AOC=22°（对顶角相等）；
故答案是：22°．
18. 已知位置如图所示，试化简:=_______________.
【正确答案】2c

【详解】【分析】根据数轴可知：a＜b＜0＜c，|b|