数学第一章 解直角三角形1.3 解直角三角形精品课件ppt

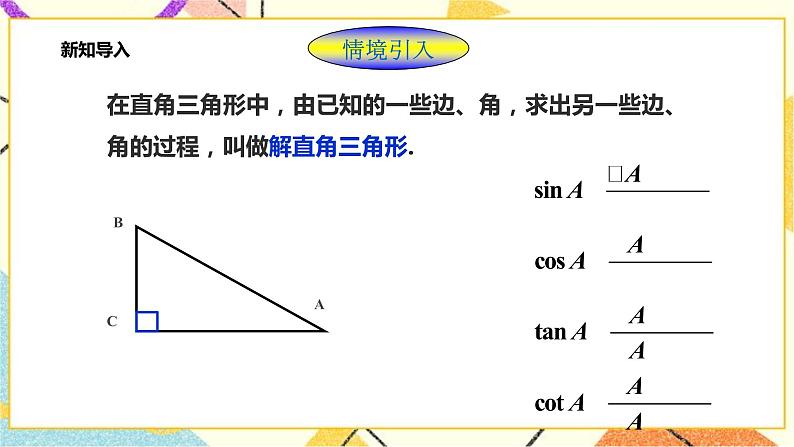
导入新课

一、创设情景，引出课题

1复习回顾：

在直角三角形中共有五个元素：边a,b,c, 锐角∠A,∠B.

这五个元素之间有什么关系？

2. 问题1.填表(一式多变,适当选用):

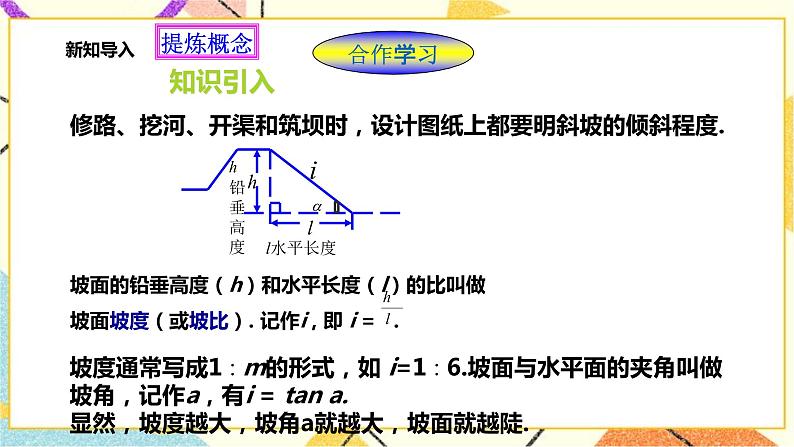
3.在修路、挖河、开渠和筑坝时，设计图纸上都要注明斜坡的倾斜程度，怎么描述倾斜程度呢？

思考

自议

利用解直角三角形解决坡度问题，体会三角函数在 实际生活中的应用；

将有关图形的计算问题化归为解直角三 角形问题来解决．

讲授新课

二、提炼概念

1. 讲解概念：

（1）坡度的概念， 如右图，这是一张水库拦水坝的横断面的设计图，坡面的铅垂高度与水平宽度的比叫做坡度(或坡比)，记作i，即i＝，坡度通常用l：m的形式，例如上图中的1：2的形式。

（2）坡面与水平面的夹角叫做坡角。从三角函数的概念可以知道，坡度与坡角的关系是i＝tanB，显然，坡度越大，坡角越大，坡面就越陡。

三、典例精讲

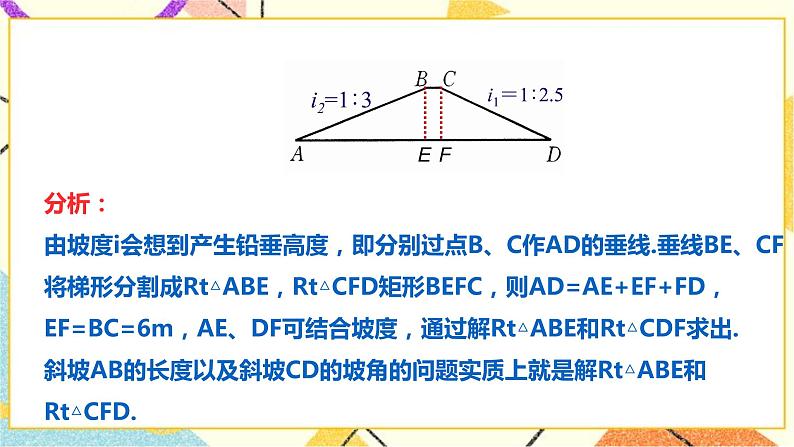
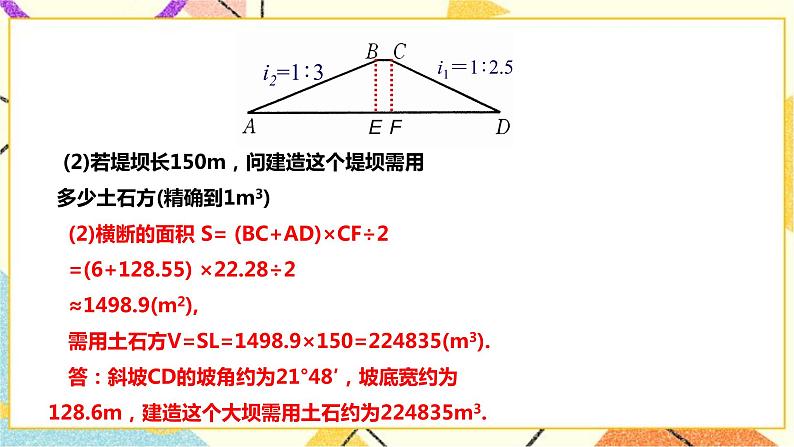
例1、一水库大坝的横断面是梯形ABCD，测得坝顶BC宽6m，斜坡CD长为60米，斜坡CD的坡度  r=1：2.5，斜坡AB的坡度i=l：3，

求：（1）斜坡CD的坡角∠D与坝底AD的宽度；(角度精确到1′，长度精确到0.1米）

    (2)若堤坝长150m，问建造这个堤坝需用多少土石方(精确到1m3)

解：（1）如图，作BE⊥AD于点E，CF⊥AD于点F．

在Rt△CDF中，

tanD＝＝＝0.4，

∴∠D≈21°48'．

∴CF＝CD×sinD＝60×sin21°48'≈22.28（m）

DF＝CD×cosD＝60×cos21°48'≈55.71（m）

∵＝，

∴AE＝3BE＝3CF＝66.84（m），

∴AD＝AE＋BC＋DF＝66.84＋6＋55.71＝128.55≈128.6（m）．

（2）设横断面面积为Sm2．

则S＝(BC＋AD)×CF＝(6＋128.55)×22.28≈1498.9（m2），

∴需用土石方V＝S∙l＝1498.9×150＝224835（m3）

答：斜坡CD的坡角约为21°48'，坡底宽约为128.6m，建造这个堤坝需用土石方224835m3．

过梯形上底的端点作梯形的高线是将有关梯形的计算问题划归为解直角三角形问题的常用辅助线，在教学后要引导学生加以总结，锐角三角形或钝角三角形的高线，也是将问题转化为，解直角三角形的常用辅助线．

例2、例4. 体育项目400M栏比赛中，规定相邻两栏架的路程为45m.在弯道处，以跑道离内侧0.3m处的弧线（图中的虚线）的长度作为相邻两栏架之间的间隔路程.已知跑道的内侧线半径为36m，问在设定A栏架后，B栏架离A栏架的距离是多少（ π取3.14，结果精确到0.1m）.

提醒： 要解决本题，先要理解弯道弧线是圆的一部分.

解：如图，连结AB，

由题意，得＝45m，OB＝36.3m．

设∠AOB＝n°，

由弧长公式l＝，可以得到n＝＝≈71.03．

作OC⊥AB于点C．

∵OA＝OB，

∴AC＝BC，∠AOC＝∠AOB＝35.52°．

∴AB＝2AC＝2OA×sin∠AOC＝2×36.3×sin35.52°≈42.2（m）．

答：设定A栏架的位置后，B栏架离A栏架的距离约为42.2m．

例4教学中可引导学生结合图形加以分析，如果有条件，可带学生到跑道上实地查看，动手实践怎样用皮卷尺确定弯道处两点间的距离，引导学生将较难测量的，弧长转化为方便测量的弦长，由此将实际问题转化为根据弧长求弦长的数学问题，而根据弧长求弦长，又可化归为用两条半径和弦AB构造等腰三角形，再作等腰三角形的高线，将求弦长的计算问题划归为解直角三角形问题来解决．联系弧长和弦长的关键量是所对的圆心角，所以首先要根据弧长的计算公式求出圆心角的度数．

对于中间运算中的量，可以不取近似值，到最后按题目要求取近似值，也可以向学生补充中间运算取近似值比结果要求多取一位的通常做法．

 搞清楚坡角、坡比(度)等各词的含义；将等腰梯形分割成矩形和直角三角形．

会将有关图形的计算问题化归为解直角三角形问题来解决.

课堂检测

四、巩固训练

1．小明沿着坡比为1∶2的山坡向上走了1 000 m，则他升高了                   (　   　)  

1.A

2.一个公共房门前的台阶高出地面1.2米，台阶拆除后，换成供轮椅行走的斜坡，数据如图所示，则下列关系或说法正确的是（　　）

A．斜坡AB的坡度是10°

B．斜坡AB的坡度是tan10°

C．AC=1.2tan10°米

D．AB=米

2.B

3．如图，是一水库大坝横断面的一部分，坝高h＝6 m，迎水斜坡AB＝10 m，斜坡的坡角为α，则tan α的值为                   (　   　)

3.D

4．如图，一段河坝的横断面是梯形ABCD，试根据图中数据，求出坡角α和坝底宽AD.

解： 过B作BF⊥AD于F.

在Rt△ABF中，AB＝10，BF＝CE＝8.∴AF＝6.

在Rt△CDE中，tan α＝＝i＝.

∴α＝30°且DE＝8，

∴AD＝AF＋FE＋ED＝6＋9＋8＝15＋8.

答：坡角α等于30°，坝底宽AD为15＋8.

5.如图所示，AB为⊙O的直径，CD⊥AB于点E，交⊙O于点C，D，OF⊥AC于点F.

(1)试说明△ABC∽△DBE；

解：(1)∵AB为⊙O的直径，∴∠ACB＝90°.

∵CD⊥AB，∴∠DEB＝90°，∴∠ACB＝∠DEB.

又∵∠A＝∠D，

∴△ACB∽△DEB.

(2)连结OC，则OC＝OA，

∴∠ACO＝∠A＝30°，

∴∠AOC＝120°.

∵OF⊥AC，∴∠AFO＝90°.

在Rt△AFO中，cos 30°＝＝，∴AO＝2.∴的长为 π·2＝π.

6.一个长方体木箱沿斜面下滑，当木箱滑至如图所示位置时，AB＝2m.已知木箱高BE＝1m，斜面坡角为 32°求木箱端点E距地面AC的高度（精确到 0.01m）.

课堂小结

1.坡度与坡角

2.应用解直角三角形知识解决实际问题的一般步骤：

（1）弄清题目中名词、术语的意义，然后根据题意画出正确的几何图形，建立数学模型；

（2）将实际问题中的数量关系转化成直角三角形各元素之间的关系，当三角形不是直角三角形时，可适当添国辅助线，得到直角三角形；

（3）解直角三角形.